Вариант 7-12
реклама
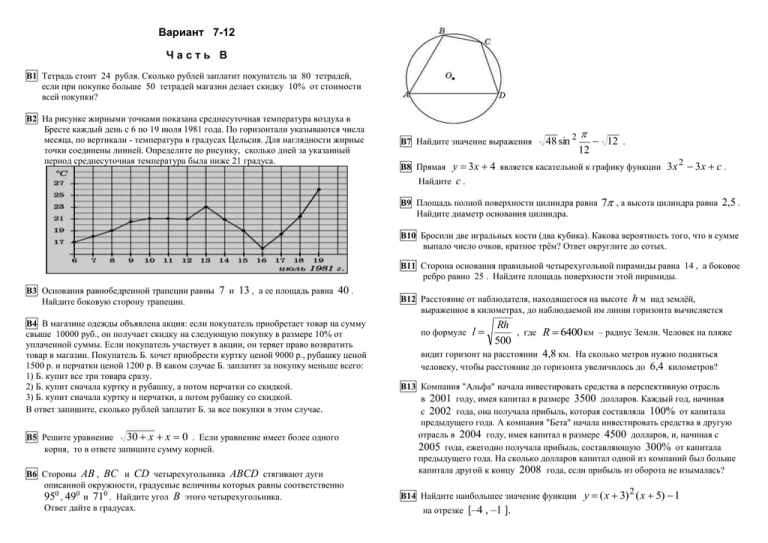
Вариант 7-12 Часть В В1 Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 80 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки? В2 На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, сколько дней за указанный период среднесуточная температура была ниже 21 градуса. В7 Найдите значение выражения 48 sin 2 12 12 . В8 Прямая y 3 x 4 является касательной к графику функции 3 x Найдите 2 3x c . c. В9 Площадь полной поверхности цилиндра равна Найдите диаметр основания цилиндра. 7 , а высота цилиндра равна 2,5 . В10 Бросили две игральных кости (два кубика). Какова вероятность того, что в сумме выпало число очков, кратное трём? Ответ округлите до сотых. В11 Сторона основания правильной четырехугольной пирамиды равна 14 , а боковое ребро равно 25 . Найдите площадь поверхности этой пирамиды. В3 Основания равнобедренной трапеции равны Найдите боковую сторону трапеции. 7 и 13 , а ее площадь равна 40 . В4 В магазине одежды объявлена акция: если покупатель приобретает товар на сумму свыше 10000 руб., он получает скидку на следующую покупку в размере 10% от уплаченной суммы. Если покупатель участвует в акции, он теряет право возвратить товар в магазин. Покупатель Б. хочет приобрести куртку ценой 9000 р., рубашку ценой 1500 р. и перчатки ценой 1200 р. В каком случае Б. заплатит за покупку меньше всего: 1) Б. купит все три товара сразу. 2) Б. купит сначала куртку и рубашку, а потом перчатки со скидкой. 3) Б. купит сначала куртку и перчатки, а потом рубашку со скидкой. В ответ запишите, сколько рублей заплатит Б. за все покупки в этом случае. В5 Решите уравнение 30 x x 0 . Если уравнение имеет более одного корня, то в ответе запишите сумму корней. В6 Стороны AB , BC и CD четырехугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 950 , 490 и 710 . Найдите угол B этого четырехугольника. Ответ дайте в градусах. В12 Расстояние от наблюдателя, находящегося на высоте h м над землёй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется Rh , где R 6400 км – радиус Земли. Человек на пляже 500 видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров? по формуле l В13 Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 3500 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 4500 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2008 года, если прибыль из оборота не изымалась? В14 Найдите наибольшее значение функции на отрезке [–4 , –1 ]. y ( x 3) 2 ( x 5) 1 Вариант 7-12 Набор 1 заданий 4. Два квадрата ABCD и AMNK , имеющие общую вершину А , расположены так, что стороны АВ и АМ образуют угол в 45 0 . Известно, что площадь пересечения квадратов равна 8,5 , а площадь их объединения равна 34,5 . Найдите площадь каждого из квадратов. Ответ: 18 и 25 . Часть С С1 а) Решите уравнение sin x sin 2x 2 cos x 1 . б) Укажите корни этого уравнения, принадлежащие отрезку 3 , . 2 С2 В прямоугольном параллелепипеде АВСТА1В1С1Т1 с рёбрами АВ = 3 АТ = 4 , АА1 = 2 найдите угол между прямыми АH и Т1Е , где Н – середина ребра СТ , а Е – середина ребра ВВ1 . 95 2 x 2 12 С3 Решите систему неравенств 2 x 5 0,25 log ( x 2) 5 log 44 2 ( x 2) 2 С4 5. На боковой стороне АВ трапеции , АВСD взята такая точка М , что АМ : ВМ = 2 : 3 . На противоположной стороне CD взята такая точка N , что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение CN : DN , если BC : AD = 1 : 2 . Ответ: 3 : 29 . 8. Окружность, проходящая через вершины B , C и D параллелограмма ABCD , касается прямой AD и пересекает прямую AB в точках B и E . Найти длину отрезка AE , если AD = 4 и CE = 5 . Ответ: 3,2 . 12. Дан прямоугольник АВСТ со сторонами АВ = 2 и ВС = выбрана точка Е так, что АЕТ СЕТ . Найдите АЕ . 3 . На прямой АВ Ответ: 1 или 3 . С4 Дан треугольник АВС со сторонами АВ = 10 , ВС = 12 , АС = 14 . АН – высота, опущенная из точки А на сторону ВС . На стороне АВ взята точка М так, что треугольник ВМН подобен треугольнику АВС . Найдите длину отрезка НМ . 15. Окружности радиусов 4 и 9 касаются друг друга и некоторой прямой, не проходящей через точку касания окружностей. Найдите радиус окружности, касающейся каждой из двух данных и той же прямой. Ответ: 1,44 или а , при каждом из которых уравнение 16. Окружности радиусов 2 и 4 касаются друг друга в точке В . Через точку В проведена прямая, пересекающая второй раз меньшую окружность в точке А , а С5 Найдите все значения параметра 1 ax x 2 8 x 15 0 имеет единственное решение. С6 Дана арифметическая прогрессия, состоящая из 32 чисел. а) Может ли эта прогрессия содержать ровно 8 целых чисел? б) Может ли эта прогрессия содержать ровно 17 целых чисел? в) Найдите наименьшее число n , при котором эта прогрессия не может содержать ровно n целых чисел. большую – в точке С . Найдите ВС , если АС = 3 2 . Ответ: 36 . 2 2 . Вариант 7-12 Ответы к заданиям части В В1 1728 В2 7 В3 5 В4 10650 В5 -5 В6 108 В7 -3 В8 7 В9 2 В10 0,33 В11 868 В12 1,4 В13 704000 Ответы и указания к заданиям части С 2k ; 2n a) С2 arccos С3 63 3 х - 2 , - - 1 , log 2 32 4 С4 7 14 или 3 5 С5 1 1 8 a , Указание: воспользуйтесь графическим методом 5 3 15 2 3 б) 5 7 5 , , , , , 2 3 3 2 3 3 С1 26 1898 С6 а) да , б) нет , в) 9 В14 15