Фестиваль «Юные интеллектуалы Среднего Урала
реклама
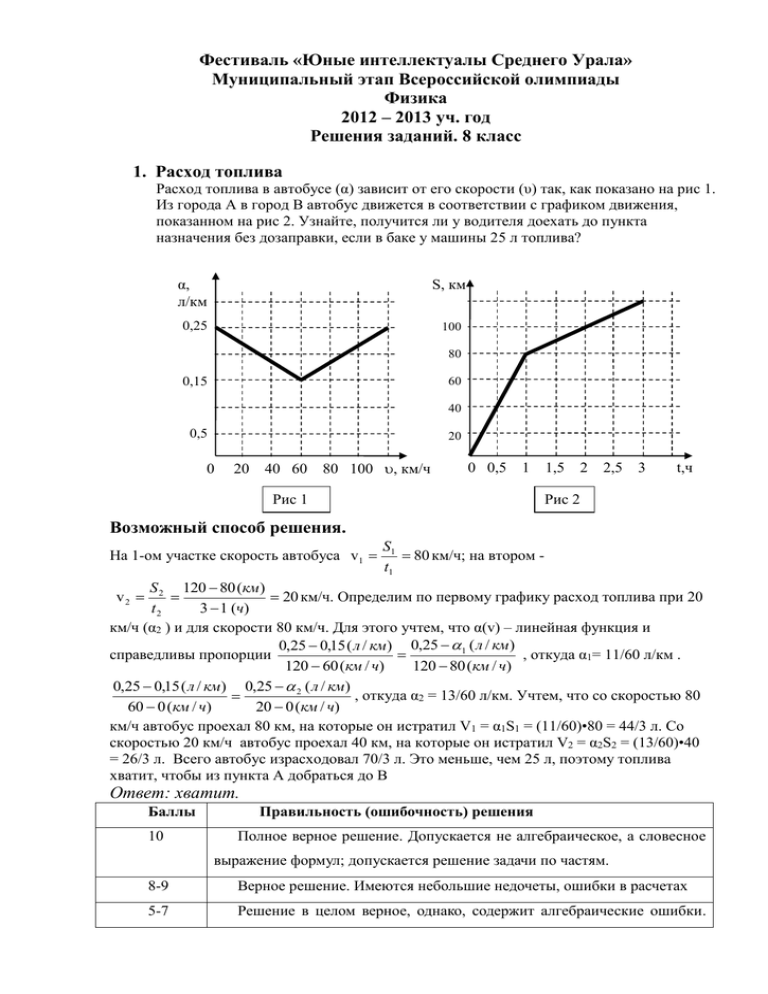
Фестиваль «Юные интеллектуалы Среднего Урала» Муниципальный этап Всероссийской олимпиады Физика 2012 – 2013 уч. год Решения заданий. 8 класс 1. Расход топлива Расход топлива в автобусе (α) зависит от его скорости (υ) так, как показано на рис 1. Из города А в город В автобус движется в соответствии с графиком движения, показанном на рис 2. Узнайте, получится ли у водителя доехать до пункта назначения без дозаправки, если в баке у машины 25 л топлива? α, л/км S, км 0,25 100 80 0,15 60 40 0,5 20 0 20 40 60 80 100 , км/ч 0 0,5 1 Рис 1 1,5 2 2,5 3 t,ч Рис 2 Возможный способ решения. На 1-ом участке скорость автобуса v1 S1 80 км/ч; на втором t1 S 2 120 80 (км) 20 км/ч. Определим по первому графику расход топлива при 20 t2 3 1 (ч) км/ч (α2 ) и для скорости 80 км/ч. Для этого учтем, что α(v) – линейная функция и 0,25 0,15 ( л / км) 0,25 1 ( л / км) справедливы пропорции , откуда α1= 11/60 л/км . 120 60 (км / ч) 120 80 (км / ч) 0,25 0,15 ( л / км) 0,25 2 ( л / км) , откуда α2 = 13/60 л/км. Учтем, что со скоростью 80 60 0 (км / ч) 20 0 (км / ч) км/ч автобус проехал 80 км, на которые он истратил V1 = α1S1 = (11/60)•80 = 44/3 л. Со скоростью 20 км/ч автобус проехал 40 км, на которые он истратил V2 = α2S2 = (13/60)•40 = 26/3 л. Всего автобус израсходовал 70/3 л. Это меньше, чем 25 л, поэтому топлива хватит, чтобы из пункта А добраться до В v2 Ответ: хватит. Баллы 10 Правильность (ошибочность) решения Полное верное решение. Допускается не алгебраическое, а словесное выражение формул; допускается решение задачи по частям. 8-9 Верное решение. Имеются небольшие недочеты, ошибки в расчетах 5-7 Решение в целом верное, однако, содержит алгебраические ошибки. Если расход примерно определен по графику, то надо ставить не более 6 баллов Есть понимание описанного в задаче процесса, но содержит ошибки в 2-4 записи необходимых для решения уравнений (в приведенном способе решения – формула для расчета скорости и формула для расчета объема топлива). Есть отдельные уравнения, относящиеся к сути задачи при отсутствии 0-1 решения (или при ошибочном решении). Решение неверное, или отсутствует. 0 2. Воздушный шар Аэронавт, путешествуя на воздушном шаре, внезапно увидел, что равномерно движется вниз. Тогда он сбросил 60 кг балласта, припасенного как раз для этого случая. Воздушный шар после освобождения от балласта стал подниматься вверх с вдвое меньшей скоростью. Считая силу сопротивления воздуха прямопропорциональной скорости шара, определите эту силу во время спуска. Возможный способ решения. Fарх Fарх Fсопр1 Fсопр2 m2 g m1 g Расставим силы, действующие на воздушный шар, когда он летит вверх и вниз (см.рис.). Условие равномерности движения: равнодействующая сил, действующих на шар равна нулю. Тогда для движения вниз имеем Fсопр+Fарх = m1g, а для движения вверх Fарх = m1g + Fсопр/2. Здесь мы учли, что Fарх не изменяется, Fсопр1 = Fсопр, а Fсопр2 = Fсопр/2, так как Fсопр. Так как сброшенный груз m = m1 – m2. Решая полученную систему, получим 3/2Fсопр=mg, откуда Fсопр = 400 Н Ответ: Fсопр = 400 Н Баллы 10 Правильность (ошибочность) решения Полное верное решение. Допускается не алгебраическое, а словесное выражение формул; допускается решение задачи по частям. 8-9 Верное решение. Имеются небольшие недочеты, ошибки в расчетах 5-7 Решение в целом верное, однако, содержит алгебраические ошибки. Неверный учет того, что сила сопротивления прямопропорциональна скорости – не более 6 баллов Есть понимание описанного в задаче процесса, но содержит ошибки в 2-4 записи необходимых для решения уравнений. В этом пункте оценивается неверная расстановка сил. Есть отдельные уравнения, относящиеся к сути задачи при отсутствии 0-1 решения (или при ошибочном решении). Решение неверное, или отсутствует. 0 3. Равновесие рычага Однородный ровный стальной прут длиной 1 м согнули пополам под углом 90о. На каком расстоянии от вершины прямого угла нужно подвесить прут, чтобы стороны получившегося угла оказались ориентированы по вертикали и горизонтали (см. рис.)? Возможный способ решения. Представим стержень как две материальные точи массами по m, расположенные в центрах обеих частей стержня (см. рис.). Тогда получится рычаг, на плечи которого действуют равные силы. Тогда и плечи этих сил равны, то есть ℓ/2 – х = х, х = ℓ/4 х = 1 м/4 = 25 см ℓ/2-х Ответ: прут надо подвесить на расстоянии 25 см от вершины прямого угла. х mg mg Баллы 10 Правильность (ошибочность) решения Полное верное решение. Допускается не алгебраическое, а словесное выражение формул; допускается решение задачи по частям. Для полного решения обязательно применение правила рычага (правила моментов) 8-9 Верное решение. Имеются небольшие недочеты, ошибки в расчетах 5-7 Решение в целом верное, однако, содержит алгебраические ошибки. 2-4 Есть понимание описанного в задаче процесса, но содержит ошибки в записи необходимых для решения уравнений. В этом пункте оценивается неверная расстановка сил. 0-1 Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении). Решение неверное, или отсутствует. 0 4. Кипятильник Электрическим кипятильником мощностью 500 Вт нагревают воду в кастрюле. За две минуты температура воды увеличилась от 85˚С до 90˚С. Затем кипятильник отключили и за одну минуту температура воды упала на один градус. Сколько воды находится в кастрюле? Возможный способ решения. Будем считать, что комнатная температура гораздо ниже рассматриваемых в задаче, поэтому можно считать тепло, уходящее от кастрюли в комнату в единицу времени (мощность отвода тепла Nпотерь)постоянной величиной, несмотря на то, что это тепло прямопропорционально разности температур кастрюли и комнатной температуры. Кроме того будем пренебрегать теплоемкостью кастрюли. Тогда при нагреве воды энергетический баланс будет выражаться Nτ1 = cmt1 + Nпотерь•τ1, а после отключения кипятильника тепловой баланс будет: cmt2 = Nпотерь•τ2. Здесь N – мощность нагревателя, m – масса воды в кастрюле t1 и t2 – это 5о С и 1оС соответственно, τ1 и τ2 - это время нагрева и охлаждения соответственно. Исключая из полученных уравнений Nпотерь получаем N 1 m 2кг 1 c t1 t 2 2 Ответ: воды в кастрюле примерно 2 кг. Баллы 10 Правильность (ошибочность) решения Полное верное решение. Допускается не алгебраическое, а словесное выражение формул; допускается решение задачи по частям. Если нет обоснования, почему мощность теплоотвода постоянна, то надо снижать на 1 балл 8-9 Верное решение. Имеются небольшие недочеты, ошибки в расчетах 5-7 Решение в целом верное, однако, содержит алгебраические ошибки. Уравнения теплового баланса должны быть записаны с учетом потерь тепла. 2-4 Есть понимание описанного в задаче процесса, но содержит ошибки в записи необходимых для решения уравнений. 0-1 Есть отдельные уравнения, относящиеся к сути задачи при отсутствии решения (или при ошибочном решении). 0 Решение неверное, или отсутствует.








