Пробный ЕГЭ (ноябрь, 2011) Вариант1 B1.

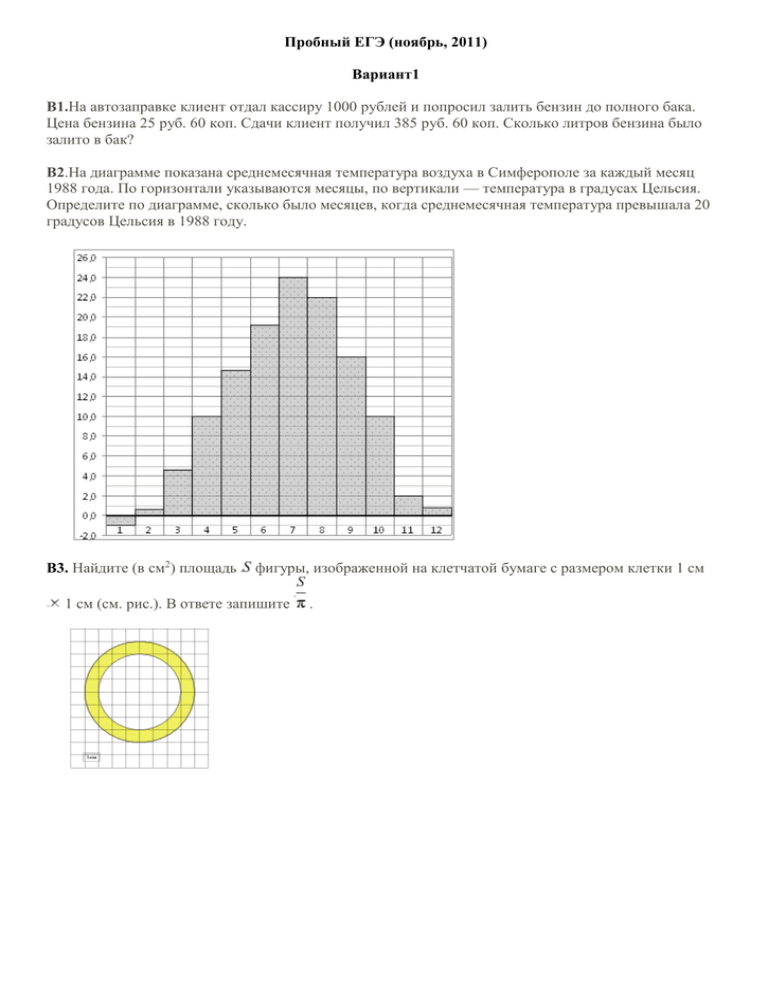
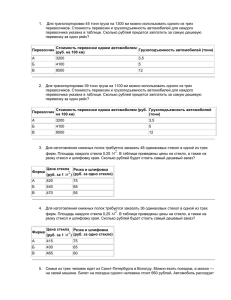
Пробный ЕГЭ (ноябрь, 2011)
Вариант1
B1.На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака.
Цена бензина 25 руб. 60 коп. Сдачи клиент получил 385 руб. 60 коп. Сколько литров бензина было
залито в бак?
B2.На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц
1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия.
Определите по диаграмме, сколько было месяцев, когда среднемесячная температура превышала 20
градусов Цельсия в 1988 году.
B3. Найдите (в см2) площадь
фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
.
B4. От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице
показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время
потребуется на дорогу? Ответ дайте в часах.
Автобусом
Электричкой
Маршрутным
такси
1
От дома до автобусной
станции — 5 мин.
От дома до станции
железной
дороги — 25 мин.
От дома до остановки
маршрутного
такси — 20 мин.
B5. Найдите корень уравнения
B6. В ромбе
угол
B7. Найдите
, если
2
Автобус в пути:
1 ч 35 мин.
3
От остановки автобуса
до дачи пешком 5 мин.
Электричка в пути:
1 ч 20 мин.
От станции до дачи
пешком 5 мин.
Маршрутное такси в
От остановки
дороге:
маршрутного такси
1ч
до дачи пешком 35 мин.
.
равен
. Найдите угол
и
. Ответ дайте в градусах
.
B8. Материальная точка движется прямолинейно по закону
, где — расстояние
от точки отсчета в метрах, — время в секундах, измеренное с начала движения. В какой момент
времени (в секундах) ее скорость была равна 6 м/с?
B9. В прямоугольном параллелепипеде
Найдите длину диагонали
известно, что
,
,
.
B10. В соревнованиях по толканию ядра участвуют 3 спортсмена из Македонии, 9 спортсменов из
Сербии, 8 спортсменов из Хорватии и 10 — из Словении. Порядок, в котором выступают
спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает
последним, окажется из Сербии.
B11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого
равны 6. Найдите объем параллелепипеда.
B12.После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения
небольших камешков в колодец и рассчитывает расстояние до воды по формуле
, где h —
расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло
.
1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось
на 0,1 с? Ответ выразите в метрах.
B13. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной
скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую
половину пути — со скоростью, на 28 км/ч большей скорости
первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость
первого автомобиля. Ответ дайте в км/ч
B14. Найдите наибольшее значение функции
на отрезке
.
Часть 2
Для записи решений и ответов на задания 1-6 используйте бланк ответов №2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
sin
x

12
sin
x

5

0 Укажите корни, принадлежащие отрезку [-  ;2 ]
C1.Решите уравнение 4
2
C2.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны
основания которой равны 3, а боковые рёбра равны 4, найдите расстояние от
точки B до прямой A1F1.
C3.Решите систему неравенств

x

5
1 

2


7
x

x

0
,



2
4

x x
9
x

20




x
8

7
x

14
8

57

C4.Прямая, перпендикулярная боковой стороне равнобедренного треугольника с
основанием, равным 12, отсекает от него четырёхугольник, в который можно
вписать окружность. Найдите площадь четырёхугольника, если радиус
окружности равен 3.
C5.Найдите все значения a, при каждом из которых наименьшее значение функции
2
f
(
x
)

2
ax

x

8
x

7
больше 1.
C6. На доске написано более 21, но менее 35 целых чисел. Среднее
арифметическое этих чисел равно −4, среднее арифметическое всех
положительных из них равно 7, а среднее арифметическое всех
отрицательных из них равно −14.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди
них?
Пробный ЕГЭ (ноябрь, 2011)
Вариант2
B1. На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака.
Цена бензина 27 руб. 60 коп. Сдачи клиент получил 6 руб. 40 коп. Сколько литров бензина было
залито в бак?
B2.На диаграмме показана среднемесячная температура воздуха в Симферополе за
каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали —
температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и
наименьшей среднемесячными температурами в 1988 году. Ответ дайте в градусах
Цельсия.
B3. Найдите (в см2) площадь
фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). В ответе запишите
.
B4. От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице
показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время
потребуется на дорогу? Ответ дайте в часах
Автобусом
Электричкой
Маршрутным
такси
1
От дома до автобусной
станции — 5 мин.
От дома до станции
железной
дороги — 25 мин.
От дома до остановки
маршрутного
такси — 10 мин.
B5. Найдите корень уравнения
B6. В ромбе
угол
B7. Найдите
, если
2
Автобус в пути:
2 ч 20 мин.
3
От остановки автобуса
до дачи пешком 10 мин.
Электричка в пути:
1 ч 50 мин.
От станции до дачи
пешком 15 мин.
Маршрутное такси в
дороге:
1 ч 5 мин.
От остановки
маршрутного такси
до дачи пешком 1 ч
25 мин.
.
равен
. Найдите угол
и
. Ответ дайте в градусах
.
B8. Материальная точка движется прямолинейно по закону
, где —
расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. В какой
момент времени (в секундах) ее скорость была равна 20 м/с?
B9. В прямоугольном параллелепипеде
. Найдите длину диагонали
известно, что
,
,
.
B10. В соревнованиях по толканию ядра участвуют 9 спортсменов из Дании, 3 спортсмена из
Швеции, 8 спортсменов из Норвегии и 5 — из Финляндии. Порядок, в котором выступают
спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает
последним, окажется из Финляндии.
B11. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1.
Объем параллелепипеда равен 5. Найдите высоту цилиндра.
B12. Некоторая компания продает свою продукцию по цене
руб. за единицу, переменные
затраты на производство одной единицы продукции составляют
руб., постоянные расходы
предприятия
руб. в месяц. Месячная операционная прибыль предприятия (в рублях)
вычисляется по формуле
. Определите наименьший месячный объeм
производства q (единиц продукции), при котором месячная операционная прибыль предприятия
будет не меньше 800000 руб.
B13. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между
которыми равно 84 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше
прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь
столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
Ответ дайте в км/ч.
B14. Найдите наибольшее значение функции
на отрезке
.
Часть2
Для записи решений и ответов на задания 1-6 используйте бланк ответов №2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.
2
cos
x

7
cos
x

5

0[-  ;2 ]
C1.Решите уравнение 6
C2.В правильной треугольной призме ABCA1B1C1, все рёбра которой равны 6,
найдите расстояние между прямыми AA1 и BC1.

4
 1 x

2
 
6
x

x

0
x

7
x

12
3

x


C3.Решите неравенство 
2
C4.Через вершину B правильного шестиугольника ABCDEF проведена прямая,
пересекающая диагональ CF в точке K . Известно, что эта прямая разбивает
шестиугольник на части, площади которых относятся как 2:3. Найдите
отношение CK:KF .
C5. Найдите все положительные значения а, при каждом из которых система уравнений
2
2

(
x

9
)

(
y

5
)

9
,

 2 2 2

(x

3
)
y
a

имеет единственное решение.
C6.Набор состоит из тридцати девяти натуральных чисел, среди которых есть
числа 3, 4 и 6. Среднее арифметическое любого тридцати одного числа этого
набора меньше 2.
а) Может ли такой набор содержать ровно шестнадцать единиц?
б) Может ли такой набор содержать менее шестнадцати единиц?
в) Докажите, что в любом таком наборе есть несколько чисел, сумма которых
равна 32.