Дом Учителя Уральского федерального округа IX
реклама
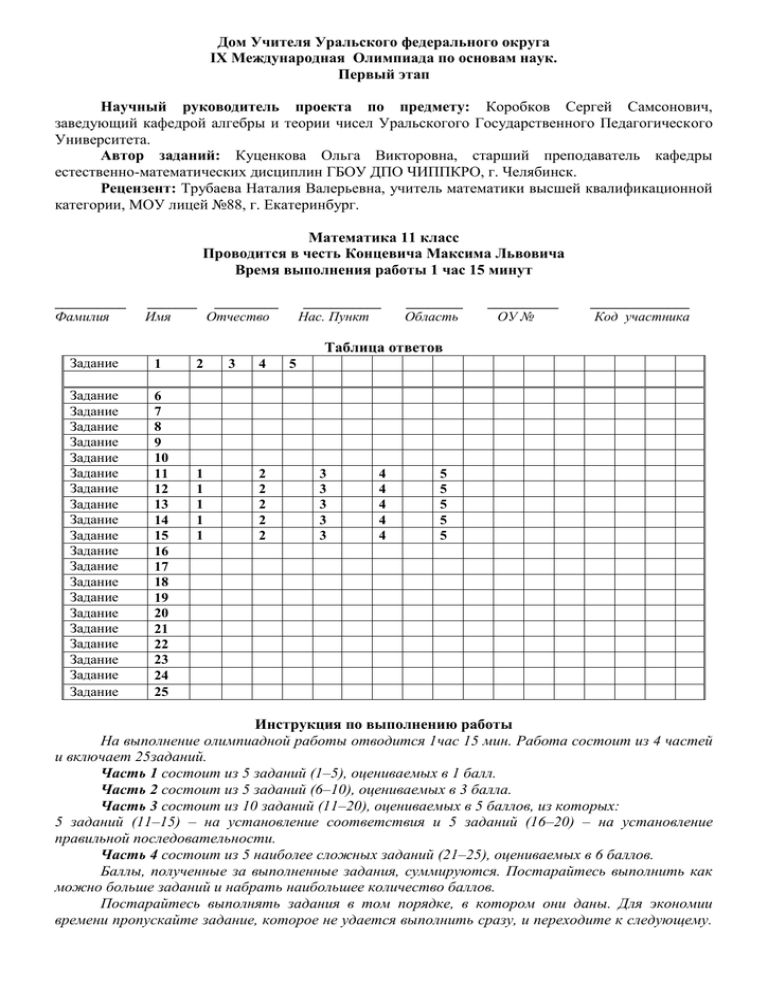
Дом Учителя Уральского федерального округа IX Международная Олимпиада по основам наук. Первый этап Научный руководитель проекта по предмету: Коробков Сергей Самсонович, заведующий кафедрой алгебры и теории чисел Уральскогого Государственного Педагогического Университета. Автор заданий: Куценкова Ольга Викторовна, старший преподаватель кафедры естественно-математических дисциплин ГБОУ ДПО ЧИППКРО, г. Челябинск. Рецензент: Трубаева Наталия Валерьевна, учитель математики высшей квалификационной категории, МОУ лицей №88, г. Екатеринбург. Математика 11 класс Проводится в честь Концевича Максима Львовича Время выполнения работы 1 час 15 минут __________ Фамилия _______ _________ Имя Отчество ___________ Нас. Пункт ________ Область __________ ОУ № ______________ Код участника Таблица ответов Задание 1 Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание Задание 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2 1 1 1 1 1 3 4 2 2 2 2 2 5 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5 Инструкция по выполнению работы На выполнение олимпиадной работы отводится 1час 15 мин. Работа состоит из 4 частей и включает 25заданий. Часть 1 состоит из 5 заданий (1–5), оцениваемых в 1 балл. Часть 2 состоит из 5 заданий (6–10), оцениваемых в 3 балла. Часть 3 состоит из 10 заданий (11–20), оцениваемых в 5 баллов, из которых: 5 заданий (11–15) – на установление соответствия и 5 заданий (16–20) – на установление правильной последовательности. Часть 4 состоит из 5 наиболее сложных заданий (21–25), оцениваемых в 6 баллов. Баллы, полученные за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Постарайтесь выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. К пропущенному заданию вы сможете вернуться после выполнения всей работы, если останется время. Ответы занесите в специальную таблицу ответов. Первая часть. Задания, оцениваемые в 1 балл В заданиях 1–5 выберите один правильный ответ из четырех предложенных и укажите его номер в таблице ответов. x 33 1 1. Сократите дробь: 33 . x x 22 x11 õ11 1) 11 õ 1 õ11 1 2) õ11 1 3) 11 õ õ11 1 4) õ11 2. Найдите значение выражения 6,8+2cos2x, если sinx=0,5. 1) 8,3 2) 7,8 3) 6,8 4) 9,3 3. Длины сторон прямоугольного треугольника равны: 1) 3 , 2 , 1 2) 3, 5 , 1 3) 3, 5 , 4 4) 3, 3, 4 4. Вычислите tg4x+ctg4x, если tgx+ctgx=5. 1) 625 2) 527 3) 125 4) 110 5. График какой функции изображен на рисунке? 1) у=2х–1,5 2) у=2х–2 3) у =2х–3 4) у=2–х–2 у 1 0 1 х Вторая часть. Задания, оцениваемые в 3 балла В заданиях 6–10 выберите три правильных ответа из шести предложенных и укажите их номера в таблице ответов. 6. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=1+12t–5t2, где h –высота в метрах, t – время в секундах, прошедшее с момента броска. Выбери верные утверждения: 1) мяч поднимется на высоту больше 8 м 2) наибольшая высота, на которую поднимется мяч – 8м 3) за 1 секунду мяч поднимется на наибольшую высоту 4) меньше 2 секунд мяч будет находиться на высоте больше 5 м 5) за первые 2 секунды мяч окажется на высоте 5 м 6) через три секунды с момента подбрасывания мяч упадет на землю 7. Олимпиада проводится в честь Концевича Максима Львовича – выдающегося французского математика, лауреата Филдсовской премии. Отметьте факты биографии Концевича М. Л. 1) М. Л. Концевич родился в 1964 году в г.Москва 2) М. Л. Концевич родился в 1964 году в Париже 3) дал своё имя интегралу (интеграл Концевича) 4) доказал теорему Концевича 5) в 2011году вошел в рейтинг журнала Форбс (Forbes) 50-ти русских, «завоевавших мир» 6) окончил Гарвардский университет 8. Выбери верные утверждения. 1) любые четыре точки лежат в одной плоскости 2) через прямую и не лежащую на ней точку проходит только одна плоскость 3) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости 4) две плоскости могут иметь только одну общую точку 5) прямая, проходящая через вершину треугольника, обязательно лежит в плоскости этого треугольника 6) три вершины треугольника принадлежат одной плоскости 9. Из пункта А в пункт В вышел пешеход, через некоторое время в этом же направлении выехал велосипедист. График движения изображен на рисунке. Выберите верные утверждения: 1) пешеход был в пути 3 часа 2) пешеход был в пути 17 часов 3) велосипедист догнал пешехода через 40 минут с момента выезда велосипедиста 4) велосипедист догнал пешехода через 1час 20 минут с момента выезда велосипедиста 5) скорость велосипедиста в два раза больше скорости пешехода 6) скорость велосипедиста в 1,5 раза больше скорости пешехода 10. Какие из равенств верны при любых значениях входящих в них букв? 2 1) a b a 2 2ab b 2 2) log a xy log a x log a y 3) à2 à a a b b 3 5) (a–b) =a3–3a2b+3ab2–b3 6) |ab|=ab 4) Третья часть. Задания, оцениваемые в 5 баллов В заданиях 11–15 установите соответствие между содержанием первого и второго столбцов. Впишите в таблицу ответы так, чтобы буква из второго столбца соответствовала цифре первого столбца. В заданиях 16–20 установите правильную последовательность. Запишите в таблицу буквы (цифры) выбранных ответов (без пробелов и других символов). 11. Установите верные равенства в логарифмических выражениях. 1) log525= А) 1 Б) 2 В) 25 Г) 5 Д) 0 2) log51= 3) (0,2)–1 +log50,2= 4) log25· log52= 5) lg500+ lg200= 12. Соотнесите график с уравнением. Уравнение 1) у=3х-2 А) 2) у=2-х Б) 3) у=3-х В) 4) ó log 1 x Г) График 2 5) y log 3 x 2 Д) 13. Установите соответствия между основными свойствами логарифмической функции y=logax, где a>0, a≠1, дополняя высказывания верными числовыми ответами. Основные свойства Числовые ответы 1) область определения функции А) (–∞; +∞) 2) множество значений B) (0; +∞) 3) функция убывает на всей своей области определения C) при a>1 4) функция возрастает на всей своей области определения D) при 0< a<1 5) график пересекает ось абсцисс E) (1;0) 14. Пусть f ( x ) 1) f(–x) 2) f ( 2 x ) 3) f ( 2 x ) 1 4) f x 5) f ( x 2) x 1 , тогда при х≠±1 установите правильное соответствие. x 1 Функция Значение функции 3 x А) 1 x õ 1 Б) õ 1 x3 В) x 1 x 1 Г) x3 Д) x 1 x 1 15. Соотнесите функцию с её наименьшим значением Функция Наименьшее значение функции 1) у=–х2–2х–1 А) –1 2) у=2sinx·cosx Б) 0 2 3) у=tg х В) невозможно определить 4) у=х2–6х+5 Г) 4 2 5) у=2sin(x) +6 Д) –4 16. Расположите в порядке возрастания числа: A) (0,1) 2 Б) (0,1)4,2 В) (0,1)π Г) (0,1)-1,3 Д) (0,1)0 17. Расположите в порядке убывания корни уравнений: A) 0,35х–2=1 Б) 7·2х=112 В) 5х=125· 5 Г) 32х–1+32х=108 Д) 5х+5х+2=26 18. Пусть f(k) – наибольший нечётный делитель чиcла k, например: f(99)=99, f(100)=25. Вычислите f(k) и запишите ответ в порядке возрастания. A) f(52) Б) f(54) В) f(51) Г) f(53) Д) f(55) 19. Установите рейтинг стоимости Интернет-трафика в 500 Мб в месяц, начиная с самого дешевого, исходя из следующих тарифных планов: Тарифный Абонентская плата Плата за трафик план A) План «0» нет 4 рубля за 1 Мб Б) План «100» 100 рублей за 100 Мб трафика в месяц 3 рубля за 1 Мб сверх 100 Мб В) План «400» 650 рублей за 400 Мб трафика в месяц 4 рубля за 1 Мб сверх 400 Мб Г) План «700» 850 рублей за 700 Мб трафика в месяц 2 рубля за 1 Мб сверх 700 Мб Д) План «1000» 1100 рублей за 1000 Мб трафика в месяц 1,5 рубля за 1 Мб сверх 10000 Мб 20. Вычислите значения выражений и расположите ответы в порядке убывания. A) tg 2 45 cos30 ctg30 Б) tg( ) ctg cos2 ( ) sin 2 В) 2 sin 22,5 cos 22,5 Г) cos( 225 ) 5 5 cos Д) 16 sin 12 12 Четвертая часть. Задания, оцениваемые в 6 баллов В заданиях 21–25 ответ записывается в таблицу ответов, начиная с первой клеточки. Каждую букву, цифру или символ пишите в отдельной клеточке, буквы должны быть печатными. Расчетные значения записываются без единиц измерения. Десятичные дроби заносятся через запятую, запятую пишите в отдельной клеточке. 21. Площадь поверхности правильной треугольной призмы равна 6. Найдите площадь поверхности призмы, если все ее ребра увеличить в три раза. 22. Найдите седьмой член геометрической прогрессии, если все члены прогрессии положительные числа, шестой член равен 15, а восьмой равен 735. 23. В слове «КАПРИЗ» переставили буквы, и получилось слово «ПРИКАЗ». Установите закономерность и сделайте такую же перестановку в слове «ЛИСТОК». В ответ запишите полученное слово. 24. Ковровая дорожка толщиной 1см свернута в рулон так, что получится цилиндр диаметром 1м. Вычислите приближенно длину дорожки в метрах, при π=3. 25. О какой единице измерения говорится в тексте: «центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 ….» .