В_9_Многогранники. Измерение геометрических величин

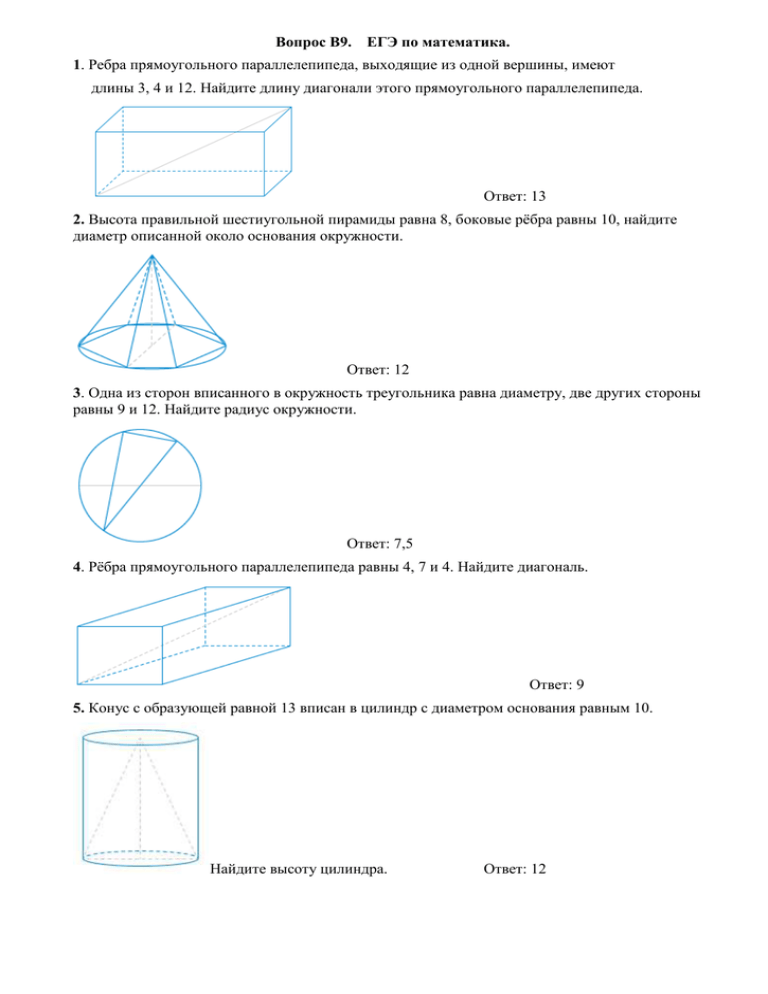
Вопрос B9. ЕГЭ по математика.
1. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, имеют
длины 3, 4 и 12. Найдите длину диагонали этого прямоугольного параллелепипеда.
Ответ: 13
2. Высота правильной шестиугольной пирамиды равна 8, боковые рёбра равны 10, найдите
диаметр описанной около основания окружности.
Ответ: 12
3. Одна из сторон вписанного в окружность треугольника равна диаметру, две других стороны
равны 9 и 12. Найдите радиус окружности.
Ответ: 7,5
4. Рёбра прямоугольного параллелепипеда равны 4, 7 и 4. Найдите диагональ.
Ответ: 9
5. Конус с образующей равной 13 вписан в цилиндр с диаметром основания равным 10.
Найдите высоту цилиндра.
Ответ: 12
6. В правильной треугольной пирамиде SABC расстояние от вершины S до точки пересечения
медиан основания P равно 8. Боковое ребро равно 17. Найдите радиус окружности, описанной
около треугольника.
Ответ: 15
7. В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50.
Найдите боковое ребро.
Ответ: 13
8. В правильной треугольной пирамиде SABC с вершиной S медиана SL треугольника SAB
равна 3. Площадь всей боковой поверхности равна 36. Найдите длину отрезка SB
.
Ответ:5
9. Рёбра прямоугольного параллелепипеда равны 2, 9 и 6. Найдите его диагональ.
Ответ: 11
10. Высота конуса равна 12, а диаметр основания — 10. Найдите образующую конуса.
Ответ: 13
11. Ребро ромба равно 15, одна из его диагоналей равна 18. Найдите другую диагональ.
Ответ: 24
12. Диагональ прямоугольного параллелепипеда равна 13, два ребра его равны 4 и 3. Найдите
третье ребро.
Ответ: 12
13. Боковые рёбра правильной шестиугольной пирамиды равны 15, диаметр описанной около
основания окружности равен 18. Найдите высоту пирамиды.
Ответ: 12
14. В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина,
SO=8, SC=17. Найдите длину отрезка BD.
Ответ: 30
15. Одна из сторон треугольника, вписанного в окружность радиуса 7,5, проходит через центр
этой окружности, другая равна 12. Найдите третью сторону треугольника.
Ответ: 9
16. В прямоугольном параллелепипеде ABCDA1B1C1D1 диагональ AC1=17, ребра AB=9, BC=8.
Найти BB1.
Ответ: 12
17. Диагональ прямоугольного параллелепипеда равна 15, два ребра равны 2 и 14. Найдите
третье ребро.
Ответ: 5
18. В правильной шестиугольной призме ADCDEFA1B1C1D1E1F1 сторона основания равна
а высота равна 3.
Найдите квадрат расстояния между вершинами B и E1.
,
Ответ: 709
19. Высота правильной шестиугольной пирамиды равна 4, диаметр описанной около основания
окружности равен 6. Найдите боковое ребро пирамиды.
Ответ: 5
20. В цилиндр вписана правильная треугольная призма, диагональ боковой грани которой
равна
. Радиус основания цилиндра равен 11. Найдите высоту призмы.
Ответ: 12
21. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 7, а
высота равна
. Найдите квадрат расстояния между вершинами B и D1
Ответ: 159
22. На круглом пьедестале установлена ёлка (конус). Высота ёлки 9,5 метров. Расстояние от
вершины ёлки до точки A, принадлежащей основанию пьедестала, равно 12 метрам. Найдите
высоту пьедестала, если радиус основания ёлки совпадает с радиусом пьедестала и
равен
метрам. Ответ дайте в метрах.
Ответ: 0,5
23. В правильной четырёхугольной пирамиде SABCD M— середина ребра BC, S — вершина.
DM=
6, SM=
. Найдите высоту пирамиды.
Вопрос B9.
ЕГЭ по математика.
1. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, имеют
длины 3, 4 и 12. Найдите длину диагонали этого прямоугольного параллелепипеда.
2. Высота правильной шестиугольной пирамиды равна 8, боковые рёбра равны 10, найдите
диаметр описанной около основания окружности.
3. Одна из сторон вписанного в окружность треугольника равна диаметру, две других стороны
равны 9 и 12. Найдите радиус окружности.
4. Рёбра прямоугольного параллелепипеда равны 4, 7 и 4. Найдите диагональ.
5. Конус с образующей равной 13 вписан в цилиндр с диаметром основания равным 10.
Найдите высоту цилиндра.
6. В правильной треугольной пирамиде SABC расстояние от вершины S до точки пересечения
медиан основания P равно 8. Боковое ребро равно 17. Найдите радиус окружности, описанной
около треугольника.
7. В правильной четырехугольной пирамиде высота равна 12. Площадь основания равна 50.
Найдите боковое ребро.
8. В правильной треугольной пирамиде SABC с вершиной S медиана SL треугольника SAB
равна 3. Площадь всей боковой поверхности равна 36. Найдите длину отрезка SB
9. Рёбра прямоугольного параллелепипеда равны 2, 9 и 6. Найдите его диагональ.
10. Высота конуса равна 12, а диаметр основания — 10. Найдите образующую конуса.
11. Ребро ромба равно 15, одна из его диагоналей равна 18. Найдите другую диагональ.
12. Диагональ прямоугольного параллелепипеда равна 13, два ребра его равны 4 и 3. Найдите
третье ребро.
13. Боковые рёбра правильной шестиугольной пирамиды равны 15, диаметр описанной около
основания окружности равен 18. Найдите высоту пирамиды.
14. В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина,
SO=8, SC=17. Найдите длину отрезка BD.
Ответ: 30
15. Одна из сторон треугольника, вписанного в окружность радиуса 7,5, проходит через центр
этой окружности, другая равна 12. Найдите третью сторону треугольника.
16. В прямоугольном параллелепипеде ABCDA1B1C1D1 диагональ AC1=17, ребра AB=9, BC=8.
Найти BB1.
17. Диагональ прямоугольного параллелепипеда равна 15, два ребра равны 2 и 14. Найдите
третье ребро.
18. В правильной шестиугольной призме ADCDEFA1B1C1D1E1F1 сторона основания равна
а высота равна 3.
Найдите квадрат расстояния между вершинами B и E1.
,
19. Высота правильной шестиугольной пирамиды равна 4, диаметр описанной около основания
окружности равен 6. Найдите боковое ребро пирамиды.
20. В цилиндр вписана правильная треугольная призма, диагональ боковой грани которой
равна
. Радиус основания цилиндра равен 11. Найдите высоту призмы.
21. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 7, а
высота равна
. Найдите квадрат расстояния между вершинами B и D1
22. На круглом пьедестале установлена ёлка (конус). Высота ёлки 9,5 метров. Расстояние от
вершины ёлки до точки A, принадлежащей основанию пьедестала, равно 12 метрам. Найдите
высоту пьедестала, если радиус основания ёлки совпадает с радиусом пьедестала и
равен
метрам. Ответ дайте в метрах.
23. В правильной четырёхугольной пирамиде SABCD M— середина ребра BC, S — вершина.
DM=
6, SM=
. Найдите высоту пирамиды.