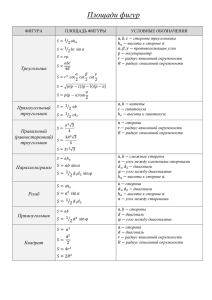
О НЕКОТОРЫХ КОНИКАХ, СВЯЗАННЫХ С ТРЕУГОЛЬНИКОМ
реклама

О НЕКОТОРЫХ КОНИКАХ, СВЯЗАННЫХ С ТРЕУГОЛЬНИКОМ В данной работе было рассмотрено несколько специальных конфигураций, связанных с кониками. Рассмотрено несколько коник, ранее не встречавшихся в работах по элементарной геометрии. Практически все из них связаны с треугольником. Были найдены доказательства существования данных коник, а так же их центры, причем в большинстве случаях получаются точки, отсутствующие в фундаментальной Энциклопедии Треугольных Центров профессора Кларка Кимберлинга (см. [5]). Теоремы, используемые в работе Теорема Карно.( см. [1],[6]) (1.1.1) Пусть А1 , А2 ВС ; В1 , В2 СА; С1 , С2 АВ . Тогда эти шесть точек лежат на одной конике, если и только если выполнено условие Карно: BA1 BA2 CB1 CB2 AC1 AC2 1 CA CA AB AB BC BC 2 1 2 1 2 1 Из этой теоремы, можно легко получить два полезных следствия, которые нам пригодятся в дальнейшем. Следствие 1 (1.1.2) Пусть шесть точек попарно расположены на прямых, содержащих стороны некоторого треугольника АВС, причем пары векторов ( BA1 , CA2 ), CB1 , AB2 и AC1 , BC 2 равны по величине и противоположны по направлению. Тогда эти шесть точек лежат на одной конике. B'2 C'1 A C1 B2 B1 C2 A'1 B A1 A2 C A'2 C'2 B'1 1 Доказательство Рассмотрим, например, «внутренний» случай («внешний» совершенно аналогичен). Пусть ВС a, CA b, AB c и BA1 CA2 x, CB1 AB2 y, AC1 BC 2 z . Тогда BA1 BA2 CB1 CB2 AC1 AC2 ( x a x ) y b y z c z 1 b y CA CA AB AB BC BC ax x y c z z 2 1 2 1 2 1 , и, в силу Теоремы 1.1, рассматриваемые точки принадлежат одной конике. Следствие 2 (1.1.3) Если шесть точек, расположенных на сторонах (или их продолжениях) некоторого треугольника можно разбить на две тройки, каждая из которых является основаниями конкурентных чевиан, то существует коника, содержащая эти шесть точек. A C2 B2 P2 C1 B1 Р1 B A1 A2 C Доказательство Следует дважды применить обратную теорему Чевы (см. [1],[2],[3],[4], [6]) , а затем воспользоваться теоремой Карно: BA1 BA2 CB1 CB2 AC1 AC2 BA1 CB1 AC1 BA2 CB2 AC2 1 1 1. CA CA AB AB BC BC CA AB BC CA AB BC 2 1 2 1 2 1 1 2 2 2 1 1 Уравнение коники в барицентрических координатах.(см. [6]) (1.2.1) В барицентрических координатах уравнение коники имеет вид: ux 2 vy 2 z 2 2 fyz 2 gzx 2hxy 0 1 И является однородным как относительно коэффициентов, так и относительно переменных, т.е. не меняется (переходит в равносильное), если все коэффициенты (или все переменные) умножить одновременно на любой постоянный ненулевой множитель. 1 2 Определение вида коники и координат центра по ее уравнению.(см. [6]) (1.2.2) Пусть уравнение коники задано: ux 2 vy 2 z 2 2 fyz 2 gzx 2hxy 0 . Введем следующие обозначения: U vw f 2 ,V wu g 2 ,W uv h 2 , F gh uf , G hf vg, H fg wh. Тогда вид коники зависит от знака выражения U V W 2F G H : Если 0 , то коника является эллипсом, если 0 - параболой, а если 0 гиперболой. Центр коники имеет координаты U G H : V F H : W F G Теорема о эллипсе растроения Рассмотрим произвольный треугольник АВС и поделим каждую из его сторон на три равные части. Тогда точки А1 , А2 , В1 , В2 , С1 , С2 лежат на конике с центром в точке M — точке пересечения медиан треугольника АВС . Причем диагонали вписанного в конику шестиугольника и отрезки соединяющие середины его противоположных сторон будут делиться этой точкой пополам. A C1 B2 A'0 C0 C2 B0 G B1 B'0 B C'0 A0 A1 A2 C Для доказательства данной теоремы, воспользуемся следствием (1.1.2) теоремы Карно, так a b c как BA1 CA2 , CB1 AB2 , AC1 BC 2 . 3 3 3 Так же, если заметить, что противоположные стороны рассматриваемого шестиугольника параллельны (по теореме Фалеса), то эту теорему можно доказать и по-другому, с помощью обратной теоремы Паскаля (см. [1], [6]), которая формулируется следующим образом: 3 Если точки пересечения прямых, содержащих противоположные стороны некоторого шестиугольника лежат на одной прямой, то его вершины лежат на одной конике. А в нашем шестиугольнике противоположные стороны параллельны - т.е., с проективной точки зрения, точки их пересечения лежат на бесконечно удаленной прямой.(см. [1],[2],[6]). Для того, чтобы доказать, что центром коники является центроид M – мы применим теорему о том, что середины пучка параллельных хорд коники лежат на прямой, проходящей через ее центр (см.[1],[6]). Очевидно, что диагональ С1 А2 параллельна АС, середина АС, точка В0 - является также и серединой В1 В2 и т.д.(по теореме Фалеса) Из теоремы Фалеса, так же следует то, что все имеющиеся в условии диагонали и отрезки делятся центроидом пополам, а из этого, то, что медианы делятся цетроидом в отношении 2:1 (см. [3],[4]). Так же из вышесказанного следует, что полученный шестиугольник является центрально симметричным, с центром симметрии в M. Теперь докажем, что наша коника действительно всегда будет представлять собою эллипс. Для этого воспользовавшись Теоремой (1.2.1), составим уравнение коники. Координаты шести наших точек имеют вид: А1 0 : CA1 : BA1 0 : 2a : a 0 : 2 : 1; A2 0 : CA2 : BA2 0 : a : 2a 0 : 1 : 2; B1 CB1 : 0 : AB1 b : 0 : 2b 1 : 0 : 2; B2 CB2 : 0 : AB2 2b : 0 : b 2 : 0 : 1; C1 BC1 : AC1 : 0 2c : c : 0 2 : 1 : 0; C2 BC 2 : AC2 : 0 c : 2c : 0 1 : 2 : 0. Теперь подставив данные координаты в уравнение коники, придем к системе из 6-ти линейных уравнений. В итоге получим u v w 4; f g h 5 , т.е. уравнение коники имеет вид: 2 x 2 2 y 2 2 z 2 5 yz 5 zx 5xy 0 . И, поскольку U V W 9 и F G H 45 , то 9 3 2 3 45 243 0 , следовательно, по Теореме (1.2.2), наша коника является эллипсом. Теорема о ортоэллипсе Из вершины А, произвольного треугольника АВС, проведем два луча, перпендикулярных АВ и АС и таких, что они не пересекают прямую ВС. Затем рассмотрим отрезок В2С1 , вписанный в угол, образованный этими лучами, причем параллельный и равный отрезку 4 ВС. Отрезки В1А2 и А1С2 определяется аналогично. Тогда, точки В2, С1, В1, А2, А1,С2 лежат на эллипсе с центром в точке Н – ортоцентре треугольника АВС. Противоположные стороны шестиугольника параллельны; диагонали его и отрезки, соединяющие середины противоположных сторон, проходят через точку Н, которой и делятся пополам. A'''0 C''1 B''2 A C''0 B''0 C''2 B''1 H B C B'''0 C'''0 A''1 A''0 A''2 Данное утверждение получается из Теоремы (2.1), если рассмотреть гомотетию, с центром в точке О – центре описанной окружности треугольника АВС с коэффициентом 2. 5 A'' B''2 C''1 A C1 C2 C''2 B B2 H G O A1 B1 A2 B''1 C C'' B'' A''1 A''2 Пусть В , С - образы точек В и С при этой гомотетии. Тогда В С || BC , поскольку при гомотетии прямые, не проходящие через ее центр, переходят в параллельные. Поэтому, опустив перпендикуляры из точек В и С на прямую ВС , получим прямоугольник с вершинами в этих точках и основаниях 1 перпендикуляров, которые обозначим А1 и A2'' . Поэтому ВА1 СА2 и А1A2'' ВС АВ . 3 Так же, так как ОВ ОС (как радиусы описанной окружности), то и ОВ ОС , как образы этих отрезков при гомотетии. Следовательно, ВВ СС и прямоугольные треугольники ВВА1 и СС А2 будут равны (по катету и гипотенузе). Значит, ВА1 СА2 . 1 1 АВ , то В А1 А1A2'' СА2 В С - т.е. точки А1 и В1 являются 3 3 образами точек А1 и А2 при рассматриваемой гомотетии. Также доказывается, что точки И, так как А1В1 В1 , В2 , С1 , С2 переходят в точки В1, В2, С1, С2 . Наконец, по самому способу построения, очевидно, что отрезки В2С1 , В1А2 и А1С2 таковы именно, какими мы представили их. То же, что центроид треугольника G указанной гомотетией переводится в ортоцентр Н, следует из факта существования прямой Эйлера. На ней лежат точки H,G,O – причем G делит отрезок НО в отношении 2:1 (см. [1],[2],[3],[4],[6].) 6 Теорема о конике задаваемой точками касания вневписанных окружностей с продолжениями сторон Пусть Ba , Ca , Cb , Ab , Ac , Bc - точки касания вневписанных окружностей с продолжениями сторон ВС, СА, АВ треугольника АВС. Тогда эти точки принадлежат одной конике, центр которой Р имеет следующие барицентрические координаты: : b a 2 a 4 2abc(b c a) b 2 c 2 P bca 2 2 4 c c 2abc(a b c) a 2 b 2 . : abc 2 2 b 4 2abc(c a b) c 2 a 2 c a b : 2 Bc Ib Cb A Ic P C0 B0 I C B A0 Ca Ba Ab Ac Ia Доказательство Обозначим за p полупериметр треугольника ABC. Для доказательства того, что указанные шесть точек лежат на конике, необходимо лишь воспользоваться Следствием (1.1.2), так как BC a CBa p a, CAb ACb p b, ABc BAc p c . (см. [1],[2],[3],[4],[6]) Координаты точек принимают вид: Ba 0 : CBa : BB a 0 : p a : p; Ca 0 : CCa : BC a 0 : p : p a; 7 Ab CAb : 0 : AAb p b : 0 : p; Cb CCb : 0 : ACb p : 0 : p b; Bc BBc : ABc : 0 p : p c : 0; Ac BAc : AAc : 0 p c : p : 0. Подставив данные координаты в уравнение коники, получим, что2 u v w 1; 2 b c a 2 f ; b c 2 a 2 c a 2 b 2 ; g c a 2 b 2 2 a b c 2 h . c a 2 b 2 Далее воспользовавшись Теоремой (1.2.2) получаем, что U 4a 2 b c 2 b c a 2 a b c 2 a b ,V 2 c a b 2 a b c 2 ,W 4c 2 a b 2 a b c 2 a b c 2 . a 2 b c F a b c 2 a b c a c b b c a a b c 2 c 2 b 2 a c 4b 2 c a 2 2 Значения G и H довольно длинные, и мы не будем их выписывать, но отметим, что G получается из F посредством циклического сдвига a b c a . И точно также из G затем получается Н. Тогда первая координата центра коники имеет вид: a 2 a 4 2abc(b c a) b 2 c 2 bca 2 4 a b c b c a c a ba b b 2 , а две другие получаются из нее циклическими сдвигами. После сокращения на общий множитель 4 a b c b c a c a b a b b 2 получаются заявленные в условии выражения для координат центра. Но данная коника, в зависимости от длин сторон треугольника может быть как эллипсом, так и гиперболой или параболой, это зависит от знака выражения U V W 2F G H (Теорема 1.2.2) Здесь и далее, в целях экономии бумаги, мы опускаем громоздкие преобразования. По ходу дела мы часто пользовались еще и однородностью коэффициентов и координат, домножая и сокращая некоторые выражения на общие множители. 2 8 4 a b c b c a c a b 2 a b c 2 2 2 b c c a a b Pa, b, c , где Pa, b, c = a 8 b 8 c 8 2 b 4 c 4 c 4 a 4 a 4 b 4 4a 2 b 2 c 2 a 2 b 2 c 2 4abc a b c 5 5 5 4 4 4 Так как знаменатель дроби положителен, знак зависит от P, при P 0 имеем эллипс, при P 0 - параболу, и при P 0 гиперболу. Ib Bc Cb A Ic C0 B0 I B Ca Ba C A0 P Ab Ia Ac Но, как позже выяснилось, центр данной коники, вместе с ней самой указаны в [5]. Эта коника была открыта 20 лет назад известным американским геометром Полем Ю (Paul Yiu), редактором замечательного журнала [7]. Теорема о конике задаваемой точками касания вписанной и вневписанных окружностей Пусть А1 , В1 , С1 , А2 , В2 , С2 - точки касания вписанной и вневписанных окружностей со сторонами ВС, СА, АВ треугольника АВС соответственно. Тогда эти точки принадлежат одной конике, центр которой Р, имеет следующие барицентрические координаты: P a 2 c b a a 3 a 2 b c b c b c a b 2 c 2 : : (две другие получаются из 2 первой циклическими сдвигами a b c a ). 9 Ib A Ic C2 C1 B1 C0 B0 P J B2 N I A0 B A1 C A2 Ia Доказательство Обозначим полупериметр треугольника ABC через p. Воспользовавшись Следствием (1.1.2) сразу получим то, что данные шесть точек лежать на конике, так как BА1 CА2 p a, CВ1 AВ2 p b, AС1 BС2 p c . (см. [1],[2],[3],[4],[6]). Далее выпишем координаты точек: А1 0 : CB1 : BB1 0 : p c : p b; A2 0 : CB2 : BB2 0 : p b : p c; B1 CB1 : 0 : AB1 p c : 0 : p a; B2 CB2 : 0 : AB2 p a : 0 : p c; C1 BC1 : AC1 : 0 p b : p a : 0; C2 BC 2 : AC2 : 0 p a : p b : 0. Подставив теперь координаты точек в уравнение коники, получим, что u v w 1; b c 2 a 2 ; b c 2 a 2 c a 2 b 2 ; g c a 2 b 2 a b 2 c 2 . h c a 2 b 2 f Далее, из Теоремы 1.2.2 получим: 10 U 4a 2 b c 4b 2 c a 2 4c 2 a b 2 ,V ,W 2 b c a 2 a b c 2 c a b 2 c b a 2 с a b 2 b c a 2 2a 4 b 4 c 4 2a 3 b c 2a 2 b 2 bc c 2 2ab 3 c 3 . F b c a 2 c a ba b c . G получается из F посредством циклического сдвига a b c a , тоже самое с Н из G. Тогда первая координата центра коники имеет вид: 4a 2 a 3 a 2 b c b c b c a b 2 c 2 2 c b a a c b b a c 2 2 , а две другие получаются из нее циклическими сдвигами. И после сокращения на общий множитель 4 b c a c a b 2 a b с 2 2 получаются выражения для координат центра, заявленные в условии. Данная точка отсутствует в Энциклопедии Треугольных Центров[5]. Данная коника может быть, в зависимости от длин сторон треугольника, как эллипсом, так и параболой или гиперболой. Когда именно она принимает тот или иной вид, зависит от знака выражения U V W 2F G H (1.2.2) 4 b c a c a b 2 a b c 2 Pa, b, c = 2 Pa, b, c , где a 6 b 6 c 6 2 a 5 b b 5 c c 5 a ab 5 bc 5 ca 5 2 a 4 bc b 4 ca c 4 ab 6a 2 b 2 c 2 3 a 4 b 2 b 4 c 2 c 4 a 2 a 2 b 4 b 2 c 4 c 2 a 4 4 b 3 c 3 c 3 a 3 a 3b 3 Поскольку знаменатель дроби положителен, P 0 имеем эллипс, P 0 параболу, P 0 гиперболу. Равноокружностный эллипс В произвольном треугольнике АВС рассмотрим следующие три пары окружностей (одинаковых в каждой паре): Первые две равные друг другу окружности вписаны в углы при вершинах В и С соответственно и касаются внешним образом друг друга. Вторые две касающиеся окружности вписаны в углы С и А. 11 Третья же пара – в углы А и В. 3. В конфигурации Пааша отметим точки Ba , Ca , Cb , Ab , Ac , Bc - точки касания соответствующих пар равных окружностей со сторонами ВС, СА, АВ соответственно. Тогда эти шесть точек лежат на одной конике, а ее центр М лежит внутри отрезка GI , соединяющего центроид треугольника с инцентром, а прямая, содержащая этот отрезок, называется прямой Нагеля, на ней также лежит и точка Нагеля N. Также, центроид G делит отрезок NI в отношении 2:1 внутренним образом (см. GM p p2 (где, p – полупериметр исходного треугольника, r – IM 3r 3S радиус вписанной в него окружности, а S – площадь). [1],[2],[3],[4],[5],[6]) и Барицентрические координаты центра имеют следующий вид: M 2 cot B C C A A B a b c cot : 2 cot cot : 2 cot cot 2 : 2 : 2 2 2 2 2 2 2 r r r a b c : : rA rB rC - где a, b, c, A, B, C - длины соответствующих сторон треугольника и величины его соответствующих углов, а rA , rB , rC - радиусы соответствующих окружностей Пааша. A Ab Ac OAc OAb Cb I Bc OBa OBc rA G rA OCb OCa r rA rA B M Ba Ca льство Пусть OBa , OCa , OCb , O Ab , O Ac , OBc - центры рассматриваемых окружностей. 3 Согласно [5], эту конфигурацию ввел геометр Иван Пааш. 12 C Доказате Очевидно, что четырехугольник OBa Ba C a OCa является прямоугольником. И O Ba Ba C a OCa rA и OBa OCa Ba Ca 2rA . Поэтому, BB a rA cot По аналогии ABc BB c cot B 2 BB a B C и CBa CCa Ba C a = rA cot 2 . C 2 2 CBa cot 2 2 BC a CC a B C C A 2 cot cot 2 cot AAc CCb 2 2 , CAb 2 2 и , , B C A A BAc ACb AAb cot cot 2 cot cot 2 2 2 2 2 cot A 2 2 B cot 2 cot BB BC a CCb CAb AAc ABc Условие Карно(1.1.1) выполняется. a CB CC AC AA BA BB a b b c c a B C C A A 2 cot cot 2 cot cot 2 2 2 2 2 2 1. C C A A B B cot 2 cot cot 2 cot cot 2 cot 2 2 2 2 2 2 cot B 2 cot Далее выпишем барицентрические координаты: Ba 0 : cot C B C B 2 : cot ; C a 0 : cot : cot 2; 2 2 2 2 С b cot C A C A : 0 : cot 2; Ab cot 2 : 0 : cot ; 2 2 2 2 Ac cot B A B A 2 : cot : 0; Bc cot : cot 2 : 0. 2 2 2 2 Подставив затем координаты точек в уравнение коники (Теорема 1.2.1), получим: u 2 cot A A B B C C cot 2 ; v 2 cot cot 2 ; w 2 cot cot 2 ; 2 2 2 2 2 2 13 f (cot C B C B cot cot 2 cot 2 ) ; 2 2 2 2 g (cot A C A C cot cot 2 cot 2 ) ; 2 2 2 2 h cot B A B A cot cot 2 cot 2 . 2 2 2 2 Сделаем замены x cot A B C 0 , y cot 0 и z cot 0 2 2 2 И по Теореме 1.2.2 получим: U 42 y z ;V 42 z x ;W 42 x y ; 2 2 2 F 4(2 y 2 z x 2 3 2 y 2 z 2 yz x8 5 y 5 z 4 yz ; G 4(2 z 2 x y 2 3 2 z 2 x 2 zx y8 5z 5x 4 zx ; H 4(2 x 2 y z 2 3 2 x 2 y 2 xy y8 5x 5 y 4 xy. Для координат центра по 1.2.2 получим М = 81 x1 y 1 z 2 y z : 81 x1 y 1 z 2 z x: 81 x1 y 1 z 2 x y Сократим на 81 x1 y 1 z и получим M 2 y z : 2 z x : 2 x y 2 cot B C C A A B cot : 2 cot cot : 2 cot cot . 2 2 2 2 2 2 Далее из полученных нами соотношений, B C C A A B a cot cot r ; b cot cot r ; c cot cot r 2 2 2 2 2 2 и B C C A A B a cot cot 2 rA ; b cot cot 2 rB ; c cot cot 2 rC , найдем еще 2 2 2 2 2 2 две формы записи координат центра: M 2 a b c a b c :2 :2 : : r r r rA rB rC Далее разберемся с коллинеарностью точек G,M,I. 14 a b c : 2 : 2 , т.е. М является центром масс системы материальных точек r r r a b c (2 ) А : (2 ) В : (2 )С . r r r M 2 Эту систему можно разбить на две подсистемы: 2 A,2 B,2C (с центром масс в G и a b c a b c 2p A, B, C (с центром в I и суммарной массой ). r r r r r Из правил группировки и рычага (см. [3]) получим, что М GI и суммарной массой 6 ) и 6 GМ 2p GM p IM . r IM 3r Применив формулу о площади треугольника через радиус вписанной окружности (см. [2],[3],[4]), полученное отношение можно переписать несколько по-другому: S ABC p r GM p p2 . IM S 3S 3 p Далее, нам остается доказать, что полученная коника действительно является эллипсом. После разложения на множители выражение Ф из Теоремы 1.2.2 примет вид: 16 (1+x) (1+y) (1+z) (3+x+y+z), следовательно наша коника будет эллипсом. Теорема о конике полученной пересечением перпендикуляров В произвольном треугольнике ABC, через точку A, проведем прямые, перпендикулярные AB и AC, через точку B, перпендикулярные BA и BC, через с перпендикулярные CA и CB. При пересечении, данные прямые образуют точки H1, H2, H3, H4, H5, H6 (которые, кстати, лежат на одной конике, центр которой — точка пересечения серединных перпендикуляров треугольника ABC). Впишем в треугольники AH2B, AH3B, AH1C, AH3C, CH5B, CH4B окружности, тогда точки касания данных окружностей с треугольником ABC лежат на одной конике, центр которой имеет следующие барицентрические координаты: b1 2 4c1 a1 1 c1 (4 c1 ) c1 2 a1 b1 c1 a1 c1 1 : ... : ...; (две другие получаются из 2 первой циклическими сдвигами a1 b1 c1 a1 ). (90 o A) (90 o B) (90 o C ) ; b1 cot ; c1 cot , ) (где a1 cot 2 2 2 15 Для доказательства, воспользуемся Теоремой Карно (1.1.1). CA2 r1 ; BA2 r1 cot CA2 (90 o B) 2 BA2 1 ; (90 o B) cot 2 По аналогии: CA1 (90 o C ) BC 1 cot ; BA1 2 AC1 BC 2 1 (90 o B ) ; cot ; 2 (90 o A) AC 2 cot 2 o AB2 AB 1 (90 A) ; 1 cot ; o CB2 2 (90 C ) CB1 cot 2 Условие Карно выполняется: 1 (90 o C ) 1 (90 o B) 1 (90 o A) cot cot cot 1 2 2 2 (90 o B) (90 o A) (90 o C ) cot cot cot 2 2 2 16 Далее выпишем барицентрические координаты: (90 o C ) (90 o B) : 1; A2 0 : 1 : cot ; 2 2 A1 0 : cot (90 o A) (90 o C ) B1 1 : 0 : cot ; B2 cot : 0 : 1; 2 2 C1 1 : cot (90 o A) (90 o B) : 0; C 2 cot : 1 : 0; 2 2 (90 o A) (90 o B) (90 o C ) , тогда подставив данные Пусть a1 cot ; b1 cot ; c1 cot 2 2 2 координаты в уравнение коники (Теорема 1.2.1), получим: u 2a1 ; v 2b1 ; w 2c1 ; f b1c1 1; g a1c1 1; h a1b1 1; Тогда, U (b1c1 1) 2 ;V (a1c1 1) 2 ;W (a1b1 1) 2 ; F a1 b1c1 2a1 (b1c1 1) a1 (b1 c1 ) 1; 2 G a1b1 c1 2b1 (a1c1 1) b1 (a1 c1 ) 1; 2 H a1b1c1 2c1 (a1b1 1) c1 (a1 b1 ) 1; 2 Тогда первая координата коники имеет вид, b1 2 4c1 a1 1 c1 (4 c1 ) c1 2 a1 b1 c1 a1 c1 1; две другие, из нее 2 получаются циклическими сдвигами a1 b1 c1 a1 . Эта точка отсутствует в Энциклопедии Треугольных Центров[5]. Данная коника может быть, как эллипсом, так и параболой или гиперболой. Когда она принимает тот или иной вид, зависит от знака выражения Ф U V W 2( F G H ) (Теорема 1.2.2) Ф 2(b1 (c1 1) a1 (b1 c1 1) c1 3) , если Ф>0 у нас эллипсом, если Ф=0 парабола, Ф<0 гипербола. Теорема о конике полученной пересечением перпендикуляров с антидополнительным треугольником Имеется треугольник ABC, построим анти проективный треугольник A’B’C’. Проведем перпендикуляры к B’C’ из вершин B и C, к A’C’ из A и C, к A’B’ из A и B. Получим шесть прямоугольных треугольников AC’1C, AB’1B, BC’2C, BA’1A, CB’2B, CA’2A. Впишем, в каждый из них окружность, тогда точки касания данных окружностей со 17 сторонами треугольника ABC, лежат на одной конике, центр которой имеет следующие барицентрические координаты: 4 x 2 yc1 zb1 x(b1c1 yz )2 yza1 z (a1b1 xy) x(b1c1 yz ) yz (a1c1 xz)2 xb1 (a1b1 xy) : ... : ...; a b1 c1 a1 (две другие получаются из первой циклическими сдвигами 1 ). x yzx где a1 , b1 , c1 – те же, что и в предыдущем случае, а x cot A B C ; y cot ; z cot ; ) 2 2 2 Для доказательства, воспользуемся Теоремой Карно (1.1.1). CA B (90 B) CA1 r1 cot ; BA1 r1 cot 1 2 2 BA1 B 2 ; (90 B) cot 2 cot По аналогии: 18 (90 C ) A (90 B) cot cot CA2 BC1 BC 2 2 2 2 ; ; ; C (90 A) AC2 B BA2 AC1 cot cot cot 2 2 2 C (90 A) cot cot AB1 AB2 2 2 ; ; (90 C ) CB2 A CB1 cot cot 2 2 cot Условие Карно выполняется: B (90 C ) A (90 B) C (90 A) cot cot cot cot cot 2 2 2 2 2 2 1 (90 B) C (90 A) B (90 C ) A cot cot cot cot cot cot 2 2 2 2 2 2 cot Выпишем барицентрические координаты точек: A1 0 : cot B (90 B) (90 C ) C : cot ; A2 0 : cot ; cot ; 2 2 2 2 B1 cot (90 C ) C A (90 A) : 0 : cot ; B2 cot : 0 : cot ; 2 2 2 2 С1 cot A (90 A) (90 B) B : cot : 0; C 2 cot : cot : 0; 2 2 2 2 Подставив координаты в уравнение коники, получим: v 2 cot A C (90 B) A B (90 C ) B C (90 A) cot cot ; w 2 cot cot cot ; u 2 cot cot cot ; 2 2 2 2 2 2 2 2 2 f cot A B C (90 C ) (90 B) cot cot cot cot ; 2 2 2 2 2 g cot B A C (90 C ) (90 A) cot cot cot cot ; 2 2 2 2 2 h cot C B A (90 A) (90 B) cot cot cot cot ; 2 2 2 2 2 (90 o A) (90 o B) (90 o C ) ; b1 cot ; c1 cot , Обозначим a1 cot 2 2 2 x cot A B C ; y cot ; z cot ; 2 2 2 19 Тогда, U 4 x 2 yb 1zc 1 - x 2 (b1c1 yz) 2 ;V y 2 zc 1 xa 1 - y 2 (a 1c1 xz) 2 ;W z 2 xa 1 yb 1 - z 2 (a 1b1 xy) 2 ; F 2xyza 1 (b1c1 yz) yz(a 1b1 xy) (a 1c1 xz), G и H находятся циклическими сдвигами a1 b1 c1 a1 x yzx Тогда первая координата коники имеет вид, 4 x 2 yc1 zb1 x(b1c1 yz )2 yza1 z (a1b1 xy) x(b1c1 yz ) yz (a1c1 xz)2 xb1 (a1b1 xy) , остальные две находятся теми же сдвигами. Данная точка отсутствует в Энциклопедии Треугольных Центров[5]. Данная коника может быть, как эллипсом, так и параболой или гиперболой. Когда она принимает тот или иной вид, зависит от знака выражения Ф U V W 2( F G H ) (Теорема 1.2.2) Ф 4 x 2 yc1zb 1 - y 2 (a 1c1 xz) 2 - x 2 (b1c1 yz) 2 - (b1a 1 yx) 2 z 2 4xc 1 y 2 za 1 4 z 2 yb 1 xa 1 2 (2 (a 1c1 xz) xzb 1 y 2 (a 1b1 xy) yxc 1z x (a 1c1 xz) y (b1c1 yz) 2x(b 1c1 yz) yza 1 (a 1b1 xy) (a 1c1 xz)yz x (a 1b1 xy) (b1c1 yz) z) , если Ф>0 у нас эллипсом, если Ф=0 парабола, Ф<0 гипербола. Теорема о «конике симметрии» В произвольном треугольнике ABC, построим анти-дополнительный треугольник A’B’C’ . Далее, отразим точку A’ относительно серединного перпендикуляра стороны CB, точку B’ относительно серединного перпендикуляра стороны AC, точку C’ относительно серединного перпендикуляра стороны AB. Получим точки A”, B”, C”. Теперь впишем окружности в треугольники AC”B, AC’B, AB’C, AB”C, CA”B, CA’B, тогда шесть точек касания данных окружностей с треугольником ABC, лежат на одной конике, центр которой имеет следующие барицентрические координаты: x y z x 2 2 y z yz y z x y z 2 : ... : ...; (две другие получаются из первой циклическими сдвигами x y z x ). 20 Для доказательства, воспользуемся Следствием 1.1.2 Теоремы Карно. Так как C B A CA2 BA1 r cot ; BC 1 AC 2 r cot ; CB1 AB2 r cot ; 2 2 2 Выпишем барицентрические координаты точек: A1 0 : cot B C C B : cot ; A2 0 : cot : cot ; 2 2 2 2 B1 cot C A A C : 0 : cot ; B2 cot : 0 : cot ; 2 2 2 2 C1 cot A B B A : cot : 0; C 2 cot : cot : 0; 2 2 2 2 Обозначим, x cot A B C ; y cot ; z cot ; 2 2 2 Подставив данные координаты в уравнение коники, получим: u v w 2; y2 c2 x2 y2 x2 c2 ;g f ;g ; xc yc xy Тогда, U - y z 2 y z 2 ; V 4y2z2 - x z 2 x z 2 ;W 4x 2 z 2 - 21 x y 2 x y 2 ; 4x 2 y 2 F 3y 2 z 2 z 4 x 2 y 2 3z 2 3x 2 z 2 x 4 y 2 z 2 3x 2 3y 2 x 2 y 4 z 2 x 2 3 y 2 ; G ; H ; 4 xyz 2 4 zyx 2 4 zxy 2 Тогда первая координата коники имеет вид, x y z x 2 2 y z yz y z x y z 2 , остальные получаются циклическими сдвигами x y z x . Данная точка отсутствует в Энциклопедии Треугольных Центров[5]. x 4 ( y z ) 2 y 2 z 2 ( y z ) 2 2 x 3 ( y z ) 3 2 xyz( y z ) 3 x 2 ( y 4 6 y 3 z 6 y 2 z 2 6 yz 3 z 4 ) Ф 4x 2 y 2 z 2 , если Ф>0 у нас эллипс, если Ф=0 парабола, Ф<0 гипербола. Теорема о конике образованной симметрией относительно тангенциального треугольника. Рассмотрим произвольный треугольник ABC. Опишем около него окружность и проведем к ней касательные, параллельные сторонам треугольника. Отразим вершины треугольника, относительно данных касательных. Получим шесть прямоугольных треугольников. Впишем в каждый из них окружность, тогда точки касания данных окружностей с треугольником ABC, будут лежать на одной конике. Для доказательства воспользуемся Следствием 1.1.2, т.к. AB2 CB1 ; BA1 CA2 ; AC1 BC 2 . Далее выпишем барицентрические координаты наших точек: 22 A1 0 : cot A A : 1; A2 0 : 1 : cot ; 4 4 B1 1 : 0 : cot С1 cot B B ; B2 cot : 0 : 1; 4 4 C C : 1 : 0; A2 1 : cot : 0; 4 4 В итоге получим: u v w 1; f sin A B C ; g sin ; h sin ; 2 2 2 A B C A Тогда первая координата центра примет вид sin 1 sin sin cos 2 , остальные 2 2 2 2 получаются циклическими сдвигами A B C A . Данная точка отсутствует в Энциклопедии Треугольных Центров[5]. 2 B C B C A Ф 4 sin sin 1 sin sin sin 1 , если Ф>0 имеем эллипс, если Ф=0 2 2 2 2 2 параболу, Ф<0 гиперболу. Литература [1]. А. Акопян, А. Заславский. Геометрические свойства кривых второго порядка. М.,МЦНМО, 2011. [2] А. Мякишев. Элементы геометрии треугольника. М., МЦНМО, 2009. [3] В. Прасолов. Задачи по планиметрии. М., МЦНМО, 2007. [4] И. Шарыгин. Геометрия. Планиметрия. (Задачник9-11). М., Дрофа, 2001. [5] Kimberling C. Encyclopedia of Triangle Centers. http://faculty.evansville.edu/ck6/encyclopedia/ [6] Yiu P. Introduction to the Geometry of the Triangle. http://math.fau.edu/yiu/GeometryNotes020402.pdf [7] ForumGeometricorum – электронный журнал, посвященный элементарной геометрии. http://forumgeom.fau.edu 23 24