Быстрое возведение, Диффи
реклама
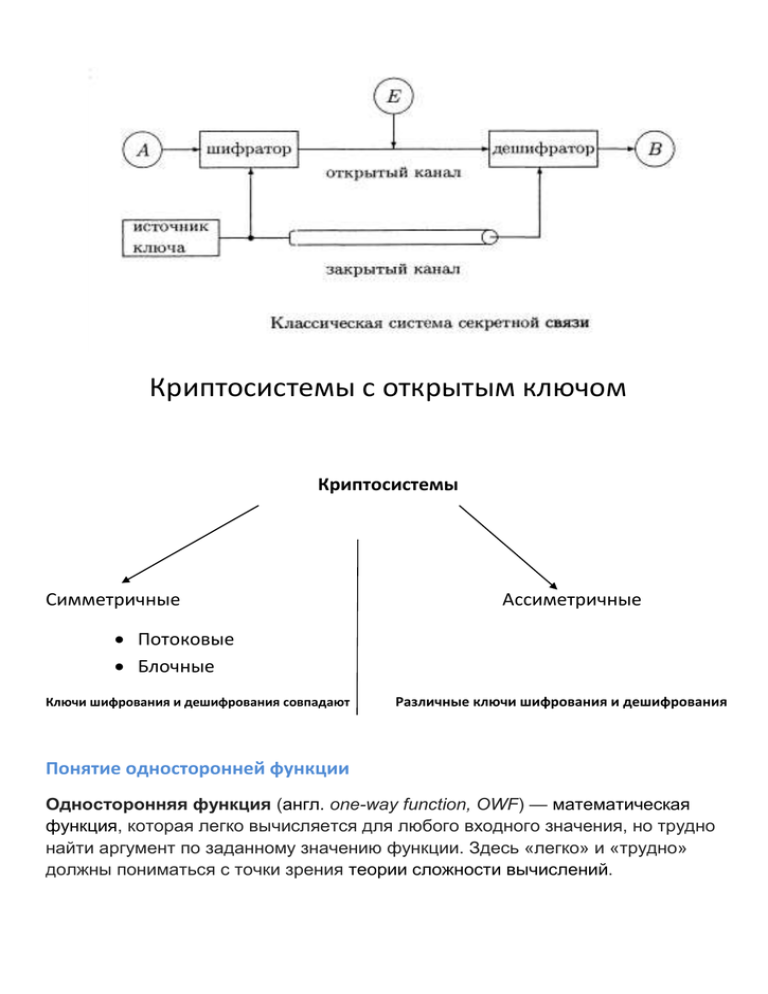
Криптосистемы с открытым ключом
Криптосистемы
Симметричные
Ассиметричные
Потоковые
Блочные
Ключи шифрования и дешифрования совпадают
Различные ключи шифрования и дешифрования
Понятие односторонней функции
Односторонняя функция (англ. one-way function, OWF) — математическая
функция, которая легко вычисляется для любого входного значения, но трудно
найти аргумент по заданному значению функции. Здесь «легко» и «трудно»
должны пониматься с точки зрения теории сложности вычислений.
Пример:
y=ax+b – не односторонняя функция, т.к. x=(y-b)/a - быстровычислима
В криптографических задачах в качестве односторонней функции часто используется
функция
y=ax mod p
Обратная функция:
x=logay mod p (дискретный логарифм)
Пример:
a=3, x=100, p=11
y=3100 mod 1, y =4
4=3x mod11, x-?
Быстрое возведение в степень
Вход:
a,x,p
Выход: ax mod p
Неподходящее решение:
Идея:
x10=<xt…x0>2
t – нижняя граница log2x
ax mod p = ax0*20+ x1*21+ x2*22+ …+xt*2t+mod p = ax0*20 * ax1*21* ax2*22 *…*axt*2t
Т.к. xi может равняться либо 0, либо 1:
axi*2i =
1, если xi = 0
a2i,если xi=1
[a1, a2, a4, a8 … и т.д.
(1)]
Следовательно,
ax mod p может быть представлено в виде произведения членов ряда (1).
Псевдокод
Получение двоичного представления числа
Операция побитового умножения:
Т.е. (9&5)=1
При побитовом умножении любого числа на единицу мы получим в
результате значение последнего бита числа:
Операция побитового сдвига
Т.е. 11 >>1 = 5
Побитовый сдвиг на один разряд вправо равнозначен целочисленному
делению операнда на 2.
Т.о. поочередно выделяя последний бит числа через операцию побитового
умножения и сдвигая его на один разряд вправо пока число не станет
равным нулю, можно получить двоичное представление числа.
<getbin.cpp>
Трудоемкость метода (в операциях умножения)
При выборе x<p трудоемкость не превосходит 2logp
6*10-13 с
1090=(103)30 = (210)30= 2300
2log22300=600
T=10-15c
1022 лет
Система Диффи-Хеллмана
Назначение
Позволяет двум или более пользователям обменяться без посредников
ключом, который может быть использован затем для симметричного
шифрования.
Описание протокола (два участника):
1. Выбирается общее простое число p и некоторое число g, 1<g<p-1, такое
что числа g1 mod p, g2 mod p … gp-1 mod p различны и образуют
множество {1…p-1}. Числа p и g известны всем абонентам.
2. Абоненты выбирают большие числа XA и XB, которые хранят в секрете.
3. Каждый абонент вычисляет:
4. Абонент A вычисляет:
Абонент B вычисляет:
ZAB=ZBA
Рекомендации по выбору g:
q – большое простое,
p=2q+1
Тогда g:
Пример.
1. q=11 => p=2*11+1=23
Пусть g=3, проверяем условие gq mod p<>1
311 mod 23=1
Пусть g=5, проверяем условие gq mod p<>1
511 mod 23=22
p=23, g=5
2. XA =7
XB = 13
3. YA =57 mod 23 = 17
YB =513 mod 23 = 21
Абонент
Секретный ключ
A
XA =7
B
XB = 13
ZAB =217 mod 23 = 10
ZBA =1713 mod 23 = 10
Открытый ключ
YA =17
YB =21






![Задача 1. Пусть f : [0,1]](http://s1.studylib.ru/store/data/002042925_1-86189856eda836731df7a59303ed5207-300x300.png)




