Концепция функции полезности
реклама
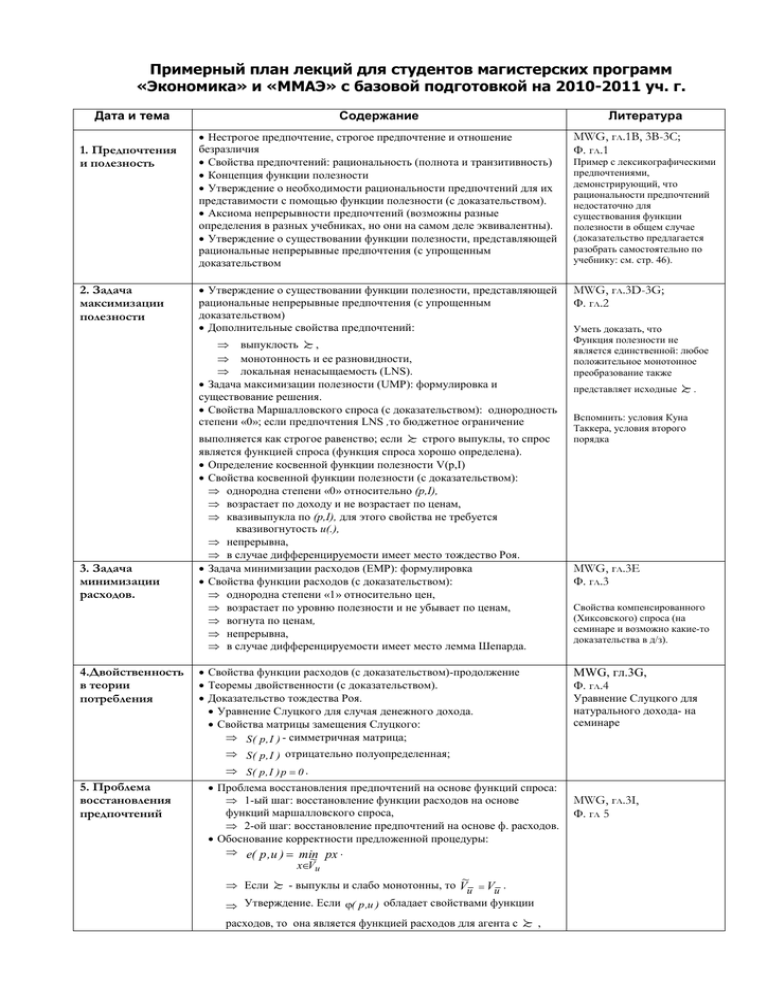
Примерный план лекций для студентов магистерских программ «Экономика» и «ММАЭ» с базовой подготовкой на 2010-2011 уч. г. Дата и тема 1. Предпочтения и полезность 2. Задача максимизации полезности Содержание Литература Нестрогое предпочтение, строгое предпочтение и отношение безразличия Свойства предпочтений: рациональность (полнота и транзитивность) Концепция функции полезности Утверждение о необходимости рациональности предпочтений для их представимости с помощью функции полезности (с доказательством). Аксиома непрерывности предпочтений (возможны разные определения в разных учебниках, но они на самом деле эквивалентны). Утверждение о существовании функции полезности, представляющей рациональные непрерывные предпочтения (с упрощенным доказательством MWG, гл.1В, 3В-3С; Ф. гл.1 Утверждение о существовании функции полезности, представляющей рациональные непрерывные предпочтения (с упрощенным доказательством) Дополнительные свойства предпочтений: MWG, гл.3D-3G; Ф. гл.2 выпуклость ~ , монотонность и ее разновидности, локальная ненасыщаемость (LNS). Задача максимизации полезности (UMP): формулировка и существование решения. Свойства Маршалловского спроса (с доказательством): однородность степени «0»; если предпочтения LNS ,то бюджетное ограничение 3. Задача минимизации расходов. 4.Двойственность в теории потребления 5. Проблема восстановления предпочтений выполняется как строгое равенство; если ~ строго выпуклы, то спрос является функцией спроса (функция спроса хорошо определена). Определение косвенной функции полезности V(p,I) Свойства косвенной функции полезности (с доказательством): однородна степени «0» относительно (p,I), возрастает по доходу и не возрастает по ценам, квазивыпукла по (p,I), для этого свойства не требуется квазивогнутость u(.), непрерывна, в случае дифференцируемости имеет место тождество Роя. Задача минимизации расходов (EMP): формулировка Свойства функции расходов (с доказательством): однородна степени «1» относительно цен, возрастает по уровню полезности и не убывает по ценам, вогнута по ценам, непрерывна, в случае дифференцируемости имеет место лемма Шепарда. Свойства функции расходов (с доказательством)-продолжение Теоремы двойственности (с доказательством). Доказательство тождества Роя. Уравнение Слуцкого для случая денежного дохода. Свойства матрицы замещения Слуцкого: S ( p , I ) - симметричная матрица; S ( p , I ) отрицательно полуопределенная; ~ представляет исходные . ~ Вспомнить: условия Куна Таккера, условия второго порядка MWG, гл.3E Ф. гл.3 Свойства компенсированного (Хиксовского) спроса (на семинаре и возможно какие-то доказательства в д/з). Уравнение Слуцкого для натурального дохода- на семинаре ~ - выпуклы и слабо монотонны, то V V . u u Утверждение. Если ( p ,u ) обладает свойствами функции расходов, то она является функцией расходов для агента с Уметь доказать, что Функция полезности не является единственной: любое положительное монотонное преобразование также MWG, гл.3G, Ф. гл.4 S( p , I ) p 0 . Проблема восстановления предпочтений на основе функций спроса: 1-ый шаг: восстановление функции расходов на основе функций маршалловского спроса, 2-ой шаг: восстановление предпочтений на основе ф. расходов. Обоснование корректности предложенной процедуры: e( p , u ) min px . ~ xVu Если Пример с лексикографическими предпочтениями, демонстрирующий, что рациональности предпочтений недостаточно для существования функции полезности в общем случае (доказательство предлагается разобрать самостоятельно по учебнику: см. стр. 46). ~ , MWG, гл.3I, Ф. гл 5 предст. множествами V~u 6.Двойственность и анализ благосостояния. Денежная оценка изменения уровня благосостояния, компенсирующая вариация ( CV ) , эквивалентная вариация, ( EV ) . Соотношение между CV , EV , CS . 7. Агрегирование в теории потребления 8. Моделирование поведения фирмы. Описание технологий. 9. Минимизация издержек и максимизация прибыли. 10. Двойственность в теории производства. Агрегирование в теории производства. 11. Основные концепции теории общего равновесия. 12. Равновесие и оптимальность в экономике с частной собственностью. Агрегирование: от индивидуального спроса к совокупному спросу: при каких условиях совокупный спрос может быть представлен как функция цен и суммарного дохода потребителей? при каких условиях совокупный спрос удовлетворяет WARP? Когда совокупный спрос представим как спрос репрезентативного потребителя? Можно ли использовать предпочтения репрезентативного потребителя для анализа благосостояния? Описание технологий: вектора чистого выпуска и производственные множества. Свойства производственных множеств: непустота, замкнутость, отсутствие рога изобилия (no free lunch), свобода расходования (free disposal), необратимость (irreversibility), выпуклость, отдача от масштаба. Максимизация прибыли и минимизация издержек: минимизация издержек- необходимое условие максимизации прибыли Задача минимизация издержек: условный спрос на факторы производства и функция издержек. Свойства функции издержек (см. свойства функции расходов) Свойства условного спроса z(w,q) (см. свойства компенсированного спроса) Функция прибыли и ее свойства: Однородность степени 1 по ценам Выпуклость Непрерывность Лемма Хотеллинга (если функция дифференцируема) Двойственность в теории производства: восстановление производственной функции на основе функции издержек. восстановление производственной функции на основе функции прибыли. Агрегирование: закон предложения Теорема о существовании репрезентативного производителя Общее равновесие: основные концепции. Допустимые распределения. Парето-оптимальные распределения. Равновесие по Вальрасу в экономике с частной собственностью. Закон Вальраса и его следствия. Первая теорема экономики благосостояния (с доказательством). Графический пример, иллюстрирующий роль предпосылки о локальной ненасыщаемости. Равновесие с трансфертами. Вторая теорема экономики благосостояния (доказательство- на следующей лекции). Роль предпосылок о выпуклости предпочтений и производственных множеств во второй теореме. Пример Эрроу. Доказательство второй теоремы экономики благосостояния MWG, гл.3I, гл. 4; Ф, гл. 6 MWG, гл. 4; Ф, гл. 6 Повторить WARP (например, см. MWG гл.2F) MWG, гл. 5В. Ф, гл. 7 MWG, гл. 5С-D. Ф, гл.8 Производственная функция. Связь между свойствами производственного множества и производственной функции (на семинаре). Уметь решать задачи минимизации расходов и максимизации прибыли. MWG, гл. 5С-Е. Ф, гл.9 MWG, гл.15, 16В Ф, гл.15-16 Повторить графическое представление экономики обмена (ящик Эджворта) и экономики Робинзона Крузо MWG, гл. 16 C-F, Ф, гл.16-17 На семинаре и самостоятельно MWG, гл. 16 F Дифференциальные характеристики паретооптимальных распределений 13.Существование равновесия по Вальрасу. 14.Единственност ь равновесия по Вальрасу 15. Ядро. Утверждение о существовании равновесного вектора в терминах избыточного спроса. Доказательство утверждения на основе теоремы Брауэра. Условия на предпочтения и запасы, при которых функции избыточного спроса будут удовлетворять вышеизложенным требованиям. Формулировка и доказательство соответствующего утверждения. Условие относительно положительности начальных запасов каждого участника можно ослабить, заменив на условие положительности совокупных начальных запасов и добавив требование строгой монотонности предпочтений. (без доказательства). Обсуждение проблемы применимости теоремы существования для экономики с производством. Единственность равновесного вектора цен в экономике с валовой заменимостью. Единственность (выпуклость множества) равновесных цен для экономики, где технологии обладают постоянной отдачей от масштаба, а избыточный спрос без производства удовлетворяет слабой аксиоме. Идея индексного подхода (если успеем) Определение ядра экономики. Пример: ядро в ящике Эджворта. Парето оптимальные распределения и ядро. Равновесные распределения и ядро. Реплицированная экономика. Пример.Реплицирование экономики обмена. Характеристика ядра с точки зрения потребительских наборов агентов одного типа (equal treatment in the core) Теорема о сжимающемся ядре (c доказательством). MWG, гл. 17C Ф, гл.18 MWG, гл. 17F-D Ф, гл.19 MWG, гл. 18A-B Ф, гл.20