Рис.5.2. Соединение генератора: а звездой, б
реклама

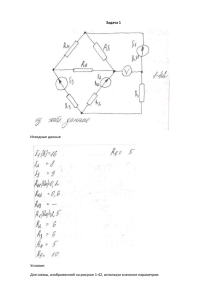
Лабораторная работа №9 СОЕДИНЕНИЕ ТРЁХФАЗНОЙ ЦЕПИ ТРЕУГОЛЬНИКОМ Цель работы – исследование различных режимов работы трёхфазной цепи с нагрузкой, соединённой в треугольник. 5.1. Общие положения 5.1.1. Основные понятия Трёхфазная система – это электрически связанная система, состоящая из трёхфазного генератора, линии передачи и трёхфазной нагрузки. Трёхфазный генератор – это генератор переменного тока с тремя обмотками на статоре, называемыми фазами и намотанными с одинаковым сдвигом в пространстве друг относительно друга на угол 120 (2 / 3) . Начала обмоток каждой фазы обозначают заглавными буквами A, B, C , а концы X , Y , Z . В силу симметрии размещения фазных обмоток величины э.д.с. фаз будут равны по модулю и сдвинуты по фазе на угол 120 . Порядок прохождения фазных э.д.с. через одинаковые значения, например, через положительные максимумы, называется порядком чередования фаз. Различают прямой и обратный порядки, векторные диаграммы которых приведены на рис.5.1. Для прямого чередования фаз справедливы соотношения: E A E Ae j A ; E C E B e j120 E Ae j 240 E Ae j120 . E B E Ae j120 ; Из последнего выражения и рис.5.1 следует, что в любой момент времени выполняется условие: E A E B E C 0. 120 E C E A б) E A а) (5.1) 120 E B E B E C Рис.5.1. Векторные диаграммы э.д.с. для прямого (а) и обратного (б) чередования фаз генератора В трёхфазной системе фазы генератора могут быть соединены либо звездой 55 (концы фаз соединены, начала фаз поданы на вход линии), либо треугольником (начало фазы подключается к концу опережающей дугой фазы), как показано на рис.5.2. а) б) A A (Z) обмотки генератора B B (X) C C (Y) N нейтральный провод Рис.5.2. Соединение генератора: а звездой, б треугольником При соединении генератора “звездой” линия передачи электрической энергии потребителю будет четырёхпроводной, при соединении “треугольником” – трёхпроводной. Нагрузка (потребитель) трёхфазной системы также может быть соединена либо треугольником, либо звездой, как показано на рис.5.3, где обозначены Za B C N Zb Zc A a Z1 Z3 b B c n Za a Zb b Z3 Z2 C Zn буквами на входе линии, строчными на выходе линии или на входе зажимы A заглавными а) Z1 Z2 Zc c б) Рис.5.3. Подключение нагрузки: а звездой, б треугольником нагрузки. Если сопротивления линий и нагрузка соответственно равны, т.e. Z a Z b Z c и Z1 Z 2 Z 3 , то нагрузка и трёхфазная система в целом называются симметричными. В этом случае при включении генератора и нагрузки звездой потенциалы точек N и n будут равными, соответственно ток по нейтральному проводу протекать не будет и от него можно отказаться, т.е. перейти к трёхпроводной линии связи. Анализ трёхфазной системы значительно упрощается при использовании топографической диаграммы, совмещённой с векторной диаграммой токов. По определению идеального генератора потенциалы точек A, B, C , N , соответствующие 56 трёхфазному генератору, не зависят от величины и характера нагрузки и на топографической диаграмме (см. рис.5.4) их положение остаётся неизменным. Потенциалы точек a, b, c, d определяются величинами токов и сопротивлений линии, которые в свою очередь зависят от величины и характера нагрузки. +j A U CA a U Aa U AB a U ab b B N +1 U BC c C Рис.5.4. Топографическая диаграмма трёхфазной системы 5.1.2. Измерение мощности в трёхфазных цепях Ваттметры измеряют активную мощность источников питания. Определим число ваттметров, необходимое для определения мощности P трёхфазного генератора. В четырёхпроводной системе, показанной на рис.5.5а, напряжения U AN ,U BN ,U CN являются фазными напряжениями на входе линии и их всегда можно приписать трём источникам напряжения E A , E B , E C , которые показаны пунктиром. Т.к. E A * E B B E C C I A * A W1 a IB * W2 * * * N IC W3 b c n I0 а) A a A U CA E C U AB U BA E B E B B C C U BC B E C * W2 * * W1 * b c б) Рис.5.5. Измерение мощности в трёхфазных цепях: а четырёхпроводной; б трёхпроводной мы имеем три источника энергии, то для измерения активной мощности в 57 четырёхпроводной схеме нам достаточно включить три ваттметра, как показано на рисунке, тогда P P1 P2 P3 . В трёхпроводной системе независимо от способа соединения фаз к измерению доступны лишь линейные напряжения U AB ,U BC и U CA . Как следует из рис.5.4, U AB U BC U CA 0 , что позволяет вместо трёх фазных генераторов ввести два эквивалентных генератора, например, E B и E C , таких, что E B U BA , E C U CA . Тогда U BC U BA U CA E B E C . Соответствующая топографическая диаграмма приведена нa рис.5.5б. Там же показана система с двумя генераторами, E B и E C , эквивалентная трёхфазной системе с тремя фазными генераторами E A , E B , E C ; эквивалентность подтверждается топографической диаграммой. Измерить мощность трёх источников E A , E B , E C при отсутствии нулевого провода не представляется возможным, а мощность генераторов в эквивалентной схеме может быть измерена, если включить два ваттметра так, как показано на рис.5,5б. Тогда мощность трёхфазного генератора будет равна: P PB PC , (5.2) где PB и PC показания ваттметров W1 и W2 на рис.5.5б. Возможны такие режимы, при которых стрелка того или иного ваттметра будет отклоняться в обратную сторону, несмотря на правильное включение ваттметра в цепь. Это соответствует случаю, когда мощность от соответствующего источника не отбирается, а поглощается источником. Для получения отсчёта следует поменять концы либо токовой, либо обмотки напряжения и измеренную мощность в выражении для подсчёта брать со знаком "минус". 5.1.3. Определение порядка чередования фаз Если даны зажимы трёхфазного генератора 1,2,3 и не известна их разметка, т.е. соответствие точкам A, B, C , то с помощью схемы на рис.5.6а можно провести разметку фаз: напряжение на лампе, которая светит более ярко, опережает по фазе напряжение на лампе, горящей тускло (в схеме, приведённой на рисунке, ярче горит лампа Л2) . Поясним этот вывод с помощью топографической диаграммы. 58 1 A 2 B A 3 C Л2 Л1 E B C N g B n g C n U An bc A U DA n U Cn U Bn C E C а) U BA б) B D в) Рис.5.6. К вопросу о разметке фаз: а принципиальная схема, б электрическая схема, в топографическая диаграмма На рис.5.6б приведена электрическая схема, эквивалентная трёхфазной трёхпроводной цепи с нагрузкой Л1,Л2,С в виде звезды. Проводимость ветвей нагрузки YA , YB , YC , причём Yb Yc g , Ya jbc . Принимая A N 0 , получим выражение для U An по методу узловых потенциалов: gE C gE B g (U BA U CA ) U DA U nN U nA , g g jbC 2 g (1 jbC / 2 g ) 1 (bC / 2 g )e j / 2 (5.3) где U DA (U BA U CA ) / 2 . Выражение (5.3) является уравнением дуги окружности, которую описывает вектор U nA при изменении bC от 0 до ∞. На топографической диаграмме рис.5.6в эта дуга обозначена DnA . Как следует из диаграммы, для любых С≠0 напряжения, приложенные к лампочкам, оказываются различными, причём U nB U nC . 5.1.4. Схема эксперимента В работе исследуется трёхфазная трёхпроводная цепь с нагрузкой, соединённой в треугольник (см. рис.5.7), когда сопротивление одной из фаз * A W1 Ia * * B Ic Za Ib V3 A6 Zb A2 Zc A4 Ica V1 W2 * a A1 c V2 A3 C Рис.5.7. Схема эксперимента 59 Z3 Z 2 Z1 A5 Ibc Iab b L C нагрузки меняется по величине и характеру. Для каждого вида нагрузки необходимо построить топографическую диаграмму, совмещённую с векторной диаграммой токов, опираясь на показания приборов. Как следует из рис.5.7, соотношения между токами в линии и фазах нагрузки задаются выражениями: IA Iab Ica ; IB Ibc Iab ; IC Ica Ibc . (5.4) Из соотношений (5.4) следует, что Ia Ib Ic 0. В качестве примера (5.5) рассмотрим порядок топографической диаграмм для трёхфазной цепи, построения векторной и в которой сопротивления линий равны нулю, а сопротивления в фазах нагрузки следующие: Z 2 Z 3 R, Z1 j / C. Из равенства нулю линейных сопротивлений следует, что потенциалы точек и A, B, C a , b, c будут попарно равны, т.е. A a , B b , C c . Соответствующая топографическая диаграмма приведена на рис.5.8а. Из неё следует, что напряжения на фазах нагрузки будут равны соответствующим линейным напряжениям на входе линии. Направления токов в фазах нагрузки устанавливаются в соответствии с направлением фазных напряжений и характером нагрузки: ток Iab опережает U ab на / 2 (линия ОМ), токи Ibc и Ica имеют ту же фазу, что и U bc и U ca (линии OK и ON соответственно); величины токов определяются показаниями амперметров A4, A5, A6 соответственно (см. рис.5.8б). Построив, таким образом, Ia Ica +J U ca U U ab В, в S Ic 0 P bc С, с Ib Iab A,a S P Ibc K Iab +I M а) N б) Рис.5.8. Топографическая (а) и векторная (б) диаграммы трёхфазной трёхпроводной цепи при Z a Z b Z c 0, Z1 j / C, Z 2 Z 3 R 60 векторы токов в фазах нагрузки, можно теперь найти векторы линейных токов согласно выражениям (5.4). Проследим поведение трёхфазной цепи при изменении величины ёмкости, т.е. сопротивления Z1 , по векторной диаграмме: фазные токи Ibc и Ica , a также линейный ток Ic остаются неизменными; ток Iab изменяется лишь по модулю – конец вектора Iab перемещается вдоль линии OM; линейные токи Ib и Ia изменяются и по модулю и по фазе концы векторов Ib и Ia перемещаются по линиям и PP соответственно. Процедура построения диаграмм усложняется, если линейные сопротивления отличны от нуля. Построение следует начинать с треугольника линейных токов, модули которых измеряются амперметрами A1, A2, A3, а направления из условия (5.5), как построение треугольника по трём сторонам, приняв, например, начальную фазу тока Ia равной нулю. Затем могут быть построены токи в фазах нагрузки на основе показаний амперметров A4, A5, A6 и соотношений (5.4). Завершив построение векторной диаграммы токов, можно приступить к построению топографической диаграммы треугольника нагрузки, приняв, например, за начало отсчёта потенциал точки "а", т.е. a 0 : строим вектор U ab (его направление определяется направлением вектора Iab и характером нагрузки Z1 , а модуль показаниями вольтметра V1 ), определив тем самым потенциал точки "в"; аналогичным образом строим вектор U bc и определяем потенциал точки "с". Если b и c определены верно, то длина образовавшегося вектора U ca должна быть равна показаниям вольтметра V 3 , а ого направление соответствовать направлению тока Ica и характеру сопротивления Z 3 . И, наконец, по векторной диаграмме линейных токов, определяющей их модули и направления, и известном характере сопротивлений в линиях, можно найти на топографической диаграмме потенциалы точек A, B, C , построив векторы падений напряжений U Aa , U Bb , U Cc . Если измерения, расчёты и построения выполнены верно, то точки A, B, C окажутся вершинами равностороннего треугольника, их чередование будет соответствовать прямому чередованию фаз, а длины векторов будут равны линейным напряжениям трёхфазного генератора. 61 U AB ,U BC ,U CA 5.2. Предварительная подготовка В процессе подготовки следует проработать литературу: / 2, § 6.9 /, /3, §§ 10.2, 10.4, 10.9 /, /4 , §§ 10.2, 10.3 / . Необходимо разобраться в порядке построения векторных и топографических диаграмм на основе экспериментальных данных, а также их использовании для анализа работы трёхфазных систем. Уясните, к каким последствиям при построении топографической диаграммы может привести не учитывание активного сопротивления катушки. 5.3. Экспериментальная и расчетная часть 1 – Собрать схему по рис.5.7, установив в плечи нагрузки активные сопротивления. Определите порядок чередования фаз с помощью трёхфазной нагрузки Л1, Л2, С, соединённых звездой. 2 – Исследование трёхфазной системы при нулевых линейных сопротивлениях: опыт 1 сопротивления в фазах нагрузки чисто активные; отрегулировать в цепи симметричный режим, снять показания приборов и на их основе построить векторную и топографическую диаграммы; опыт 2 в условиях опыта 1 разорвать линию Аа, снять показания приборов и на их основе построить векторную и топографическую диаграммы; опыт 3 в cсхеме опыта 1 с помощью сопротивлении Z1 менять ток Iab , снимая каждый раз показания амперметров; по результатам построить векторную диаграмму токов; опыт 4 в схеме по опыту 3 заменить активное сопротивление в фазе ав на индуктивное; снять показания приборов для нескольких значений индуктивности и построить на их основе векторную диаграмму токов; опыт 5 в схеме по опыту 4 вместо индуктивного сопротивления включить батарею конденсаторов; снять показания приборов при нескольких значениях ёмкости и на их основе построить векторную диаграмму токов. Для опытов 3, 4, 5 определить мощность потребителя методом двух ваттметров. Рассчитать активную мощность по показаниям амперметров и вольтметров и сравнить с экспериментальными данными. 62 3 Исследование трёхфазной цепи при ненулевых линейных сопротивлениях: установить активные сопротивления в треугольнике нагрузок и в линиях Аа, Вв, а в линию Сс включить индуктивное сопротивление. Величины сопротивлений должны обеспечивать попадание токов и напряжений цепи в диапазон измерительных приборов, а значения линейных сопротивлений должны быть известны. Снять показания приборов и на их основе построить векторную диаграмму токов и топографическую диаграмму. 5.4. Анализ результатов На основе экспериментальных данных проанализировать работу трёхфазной трёхпроводной системы при изменении фазных и линейных сопротивлений. 5.5. Перечень контрольных вопросов 1. Объяснить принцип разметки фаз с помощью двух лампочек равного сопротивления и конденсатора, соединенных звездой. 2. Показания каких амперметров изменятся, если меняется активное сопротивление в одной из фаз? 3. Нарисовать векторную диаграмму токов цепи при: разрыве в линейном проводе; разрыве в фазном проводе. 4. Как графически найти линейные напряжения эксперименте, используя результаты измерений? 63 генератора в последнем