Анализ ряда динамики
реклама

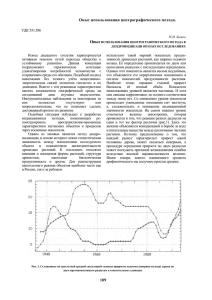
2 Анализ ряда динамики На основании приведённых в табл.1. данных о величине уровней динамического ряда в период 1990-1997 год рассчитаем показатели сравнения уровней, средние значения показателей, а также дать интервальный прогноз, ожидаемого уровня 1998года с вероятностью, равной 0,99 (ряд интервальный). Таблица 1 Ряд динамики Время, г. Уровни 1990 360 1991 380 1992 391 1993 402 1994 423 1995 440 1996 455 1997 470 1.Определим абсолютные базисные и цепные приросты, коэффициенты роста, темпы прироста и абсолютное значение 1% прироста: а) Абсолютный базисный и цепной прирост вычисляются следующим образом: Δбi =Yi-Y0; где Yi- данный уровень;Y0-уровень, принятый за базу сравнения; Δцi=Yi-Yi-1; где Yi- данный уровень;Yi-1- уровень, предшествующий данному уровню. Приведём пример расчёта абсолютного базисного и цепного прироста уровня 1992 года: Δб1992=391-360=31 Δц1992=391-380=11 б) Коэффициент роста, цепной и базисный, рассчитывается по следующей формуле: Крбi=Yi/Y0; где Уi- данный уровень;Y0-уровень, принятый за базу сравнения; Крцi=Yi/Yi-1; где Yi-уровень;Yi-1- уровень, предшествующий данному уровню. Рассчитаем базисный и цепной коэффициент роста на примере уровня 1992: Крц1992=391/380=1,029 Крб1992=391/360=1,086 в) Темпы прироста вычисляются так: Тпрi=100%(Кр-1); 3 где Кр-коэффициент роста. Например, вычислим темп прироста, базисный и цепной, для уровня 1992: Тбпр1992=100%(1,086-1)=8,6% Tцпр1992=100%(1,029-1)=2,9% г) Абсолютное значение 1% прироста вычисляется следующим образом: Аiц=Δiц/Тпрiц; где Δiц- абсолютный цепной прирост; Тпрiц- цепной темп прироста. Приведём пример вычисления абсолютного значения 1% прироста на 1992 год: А1992ц=11/2,9%=3,8(%)-1 Результаты расчётов показателей сравнения уровней приведены в табл.2. Таблица 2 Показатели сравнения уровней и их средние значения Время, г. Абсолютный прирост Уровень 1990 1991 1992 1993 1994 1995 1996 1997 Среднее значение 360 380 391 402 423 440 455 470 415,1 цепной 20 11 11 21 17 15 15 базисный 20 31 42 63 80 95 110 15,7 Коэффициент Темп прироста роста цепной базисный цепной базисный 1,056 1,056 5,6 5,6 1,029 1,086 2,9 8,6 1,028 1,117 2,8 11,7 1,052 1,175 5,2 17,5 1,040 1,222 4,0 22,2 1,034 1,264 3,4 26,4 1,033 1,306 3,3 30,6 1,039 3,9 Аiц 3,60 3,80 3,90 4,04 4,25 4,41 4,50 4,03 2.Определение средней величины уровня динамического ряда, абсолютного прироста, коэффициента роста, темпа прироста и абсолютное значение 1% прироста. Среднее значение уровней интервального динамического ряда определяется: у=Σ yi/k+1; где y- среднее значение уровней ряда динамики, yi- данный уровень, k- количество уровней ряда динамики. y=(360+380+391+402+423+440+455+470)/8=415,1 Среднее значение коэффициента роста вычисляется по следующей формуле: Кр=7√П Крц; где Кр- среднее значение коэффициента роста, Крц- цепной коэффициент роста. Кр=7√1,056*1,029*1,028*1,052*1,04*1,034*1,033= 7√1,31=1,039 Среднее значение темпа прироста определяется так: Тпр=100%(Кр-1); 4 где Тпр- среднее значение темпа прироста, Кр- среднее значение коэффициента роста. Тпр=100%(1,039-1)=3,9% Среднее значение абсолютного прироста определяется: ∆=∑∆iц/k; где ∆- среднее значение абсолютного прироста, ∆iц- цепной абсолютный прирост, kколичество уровней. ∆=(20+11+11+21+17+15+15)/7=15,7 Средняя величина абсолютного значения 1% прироста определяется: А=∆/Тпр; Где А- средняя величина абсолютного 1% прироста, ∆- среднее значение абсолютного прироста, Тпр- среднее значение темпа прироста. А=15,7/3,9=4,03 Значения средних величин приведены в табл.2. 3.Построение графического изображения ряда динамики и произведём сглаживание уровней методом “скользящей средней” по трём уровням. исходный ряд сглаживание методом “скользящей средней” аналитическое сглаживание Рис.1. Графическое изображение ряда динамики Приведём вычисления сглаживания уровней методом “скользящей средней” по трём уровням: y*1991=(360+380+391)/3=377 y*1992=(380+391+402)/3=391 y*1993=(391+402+423)/3=405,3 y*1994=(402+423+440)/3=421,7 y*1995=(423+440+455)/3=439,3 5 y*1996=(440+455+470)/3=455 4.Произведём аналитическое выравнивание ряда динамики, используя линейную трендовую модель. yt=b0+b1*t-уравнение тренда; где уt- теоретический уровень, t- условное обозначение времени, b0 и b1-коэффициенты, где b0=∑yi/(k+1); b1=∑yi*ti/∑t2i Вычислим значения b0 и b1: b0=(360+380+391+402+423+440+455+470)/8=415,1 b1=(-2520-1900-1173-402+423+1320+2275+3290)/(49+25+9+1+1+9+25+49)=1313/168=7,8 Отсюда получаем уравнение тренда: yt=415,1+7,8*t Полученные результаты представлены в табл.3. Таблица 3 Аналитическое выравнивание ряда динамики Год Уровень, уi 1990 1991 1992 1993 1994 1995 1996 1997 360 380 391 402 423 440 455 470 Итого 3321 Условное обозначение времени, ti -7 -5 -3 -1 +1 +3 +5 +7 0 yt Теоретический уровень,уt 49 25 9 1 1 9 25 49 -2520 -1900 -1173 -402 423 1320 2275 3290 360,5 376,1 391,7 407,3 422,9 438,5 454,1 469,7 0,25 15,21 0,49 28,10 0,01 2,25 0,81 0,09 168 1313 3321 47,21 t2 i (yt-yi)2 5.Рассчитаем точечный и интервальный прогноз 1998 года. Так как значение t на 1997 год +7 (см. табл.3), то соответственно значение t на 1998 год будет равным +9. Применяя полученное в п.4 уравнение тренда и t=+9, мы можем дать точечный прогноз: y1998=415,1+7,8*(+9)=485,3 Для того чтобы прогноз был правильным, его необходимо дополнить доверительным интервалом. Для этого подсчитывается остаточное среднеквадратичное отклонение от тренда: S=√∑(yi-yt)2/((k+1)-m); где yi-фактическое значение уровня, yt- теоретическое значение уровня, m- число параметров в уравнении(m=2) S=√47,21/(7+1-2)=2,8 ts=3,71 при P=0,99 y1998=yt+-ts*S y1998=485,3+-3,71*2,8=485,3+-10,4 474,9<y1998<495,7 6 Список используемой литературы: 1.Лекции по статистике. Ю.Ф.Сидохин 2.''Общая теория статистики. Статистическая методология в изучении коммерческой деятельности'' под редакцией О.Э.Башиной, А.А.Сперина; Москва 2002г. 7