Лаб_Лин_програм
реклама

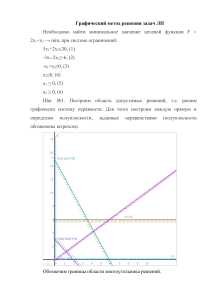
Линейное программирование Цель. Овладеть практическими навыками формулирования задач линейного программирования в соответствии с требованиями программы, их решения и интерпретации результатов. Прежде чем приступать к выполнению лабораторных работ, студент должен пройти инструктаж по технике безопасности при работе на компьютерах, внимательно изучить лекционный материал, обратиться к преподавателю за пояснениями положений, вызывающих затруднения, и дать удовлетворительные ответы на предложенные преподавателем контрольные вопросы. Далее следует внимательно и полностью прочитать содержание задания к лабораторной работе и методические указания к ней. Если какиелибо положения задания или методических указаний вызывают затруднения, студент обязан обратиться к преподавателю за консультацией. 1. 2. 3. 4. Постановка задачи; Построение допустимой области; Ввод данных в MS Excel. Решение задачи Построение допустимой области Определение. Допустимая область – эта такая область, где одновременно выполняются все ограничения задачи. Другие названия – область допустимых решений (ОДР); область работоспособности (техническое определение допустимой области). Решение. 1. Заменяем неравенства равенствами. 2. Разрешаем относительно переменной x2, получаем уравнения прямых (можно и относительно переменной x1). 3. Строим график первого уравнения (прямая делит плоскость на две части) и определяем ту часть плоскости, где выполняется первое неравенство. 4. Строим график второго уравнения (прямая делит плоскость на две части) и определяем ту часть плоскости, где выполняется второе неравенство. Выделяем область, где одновременно выполняются оба неравенства и т.д. Пусть имеются следующие ограничения: 1) 2x1+3x2 ≥4; 2) 2x1-3x2 ≤10; 3) 5x1+3x2 ≤30; 5) 4x2 ≤12; 6) x1≥0; x2≥0. Из последних двух неравенств следует, что x1 и x2 принимают неотрицательные значения и определяют первый квадрант в декартовой системе координат. Берём 1-е неравенство 2x1+3x2 ≥4 и преобразуем в равенство 2x1+3x2 =4. Выражаем x2 через x1 . В результате получим уравнение x2=(4-2x1)/3. Аналогично делаем для других ограничений: x2=(-10+2x1)/3; x2=(30-5x1)/3; x2=3. Рис. 1. Таблица значений функций-ограничений Рис. 2. Графики функций-ограничений Копируем график и вставляем в Paint. Определяем область ОДР и закрашиваем её (см. рис. 3). Как это делается? Берём первое неравенство и определяем область, где это неравенство выполняется. Возьмём, например, x1=0; x2=0 и подставим в первое неравенство. Получим 0≥4. Неравенство нарушено, следовательно, область лежит выше прямой 1. В учебной литературе на линии наносят стрелочки и/или штриховку для того чтобы указать область, где это неравенство выполняется. Мы на линии наносим короткие отрезки в сторону выполнения неравенства. Аналогично исследуем другие неравенства. В результате получим область ОДР (см. рис. 3). Рис. 3. Область допустимых решений ОДР Задания Вариант 16. Решение F(x)=7x1+5x2 → max Ограничения: 2x1+3x2≤19; 2x1+x2≤13; 3x2≥15; x1≥0; x2≥0. Решаем в MathCad Переводим ограничения в равенства и строим графики полученных функций и прямые, соответствующие целевой функции для С=21 и 39: 7x1+5x2=21 (f0(x)) и 7x1+5x2=39 (f(x). Рис. Рис. ОДР задачи №16 Рис. ОДР задачи №16 (график увеличен) Вариант 1 (16.233) (задача на дом). В цехе площадью 74 м2 необходимо установить станки, на приобретение которых отпущено 42 тыс. руб. Существует два типа станков. Станок первого типа стоимостью 6 тыс. руб., требующий 12 м2 производственных площадей, обеспечивает изготовление 70 изделий в смену. Аналогичные характеристики станка второго типа составляют соответственно 4 тыс. руб., 6 м2, 40 изделий в смену. Найти оптимальный вариант приобретения станков, обеспечивающий максимальное производство изделий в цехе. Ответ: (3; 6) Вариант 2. Для выпуска двух видов продукции требуются затраты сырья, рабочего времени и оборудования. Исходные данные приведены в таблице. Нормы затрат ресурсов на Наличие единицу продукции ресурсов 1 2 Тип ресурса Сырьё 3 5 60 Рабочее время 22 14 400 Оборудование 10 14 128 Прибыль на единицу продукции 30 25 Найти оптимальный план максимальную прибыль. выпуска продукции, обеспечивающий Вариант 3. Для изготовления двух видов изделий A, B используется токарное, фрезерное и сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени каждого из типов используемого оборудования, а также прибыль от реализации одного изделия данного вида. Тип оборудования Затраты времени (станко- Общий фонд часов) на обработку рабочего времени одного изделия вида оборудования A B (ч) Фрезерное 2 4 120 Токарное 1 8 280 Сварочное 7 4 240 Шлифовальное 4 6 360 100 140 Прибыль реализации (руб.) от Определить, сколько изделий каждого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Вариант 4. Для выпуска двух видов продукции требуются затраты сырья, рабочего времени и оборудования. Исходные данные приведены в таблице. Нормы затрат ресурсов единицу продукции 1 2 на Наличие ресурсо в Сырьё 4 3 200 Рабочее время 1 2 80 Оборудование 2 2 130 Тип ресурса Прибыль на единицу 60 продукции Найти оптимальный план максимальную прибыль. 80 выпуска продукции, обеспечивающий Вариант 5. Для обработки деталей А, В используются станки I, II и III. В таблице указаны нормы затрат времени на обработку станком соответствующей детали, продажная цена единицы детали (в руб.), стоимость 1 ч работы станка и предельное время работы станка: Детали Нормы времени Стоимость Предельное время работы станка Станки А В I 0,2 0,1 30 40 II 0,6 0,3 10 60 III 0,2 0,1 20 30 Цена 10 16 Решить задачу определения оптимальной производственной программы, максимизирующей стоимость продукции. Вариант 6. Кондитерская фабрика для производства двух видов карамели A, B использует три вида основного сырья: сахар, патоку и фруктовое пюре. Нормы расхода сырья каждого вида на производство 1т карамели приведены в таблице. В ней же указано общее количество сырья каждого вида, которое может быть использовано фабрикой, а также приведена прибыль от реализации 1т карамели данного вида. Нормы расхода сырья (т) на 1 т Общее карамели количество сырья (т) A B Вид сырья Сахар 0,8 0,5 800 Патока 0,4 0,4 600 - 0,1 120 108 112 Фруктовое пюре Прибыль от реализации 1т продукции (дол.) Найти план производства карамели, обеспечивающий максимальную прибыль от ее реализации. Вариант 7. На швейной фабрике для изготовления двух видов изделий может быть использована ткань трех артикулов. Нормы расхода ткани на пошив одного изделия приведены в таблице. В ней же указаны имеющиеся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида. Артикул ткани Норма расхода ткани (м) на одно Общее изделие вида количество ткани (м) 1 2 I 1 - 180 II - 1 210 III 4 2 800 Цена одного изделия (дол.) 9 6 Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной. Вариант 8. Предприятие выпускает два вида продукции и использует три типа основного оборудования: токарное, фрезерное и шлифовальное. Затраты времени на изготовление единицы продукции для каждого из типов оборудования приведены в таблице. В ней же указаны общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия данного вида. Определить такой объем выпуска каждого из изделий, при котором общая прибыль от их реализации является максимальной. Тип оборудования Затраты времени (станко-часов) Общий ресурс на единицу продукции вида рабочего времени (станко-часов) 1 2 Токарное 1 3 300 Фрезерное 2 1 180 Шлифовальное 1 - 340 Прибыль от реализации (руб.) 2 3 Вариант 9. Для изготовления 2-х видов изделий A, B используется токарное, фрезерное, сварочное и шлифовальное оборудование. Затраты времени на обработку одного изделия для каждого из типов оборудования указаны в таблице. В ней же указан общий фонд рабочего времени, а так же прибыль от реализации 1го изделия каждого вида: Тип оборудования Затраты времени (станко-часы) на Общий фонд обработку одного вида изделия рабочего времени (ч) A B Фрезерное 2 4 120 Токарное 1 8 280 Сварочное 7 4 240 Шлифовальное 4 6 360 Прибыль 10 14 Требуется определить, сколько изделий каждого вида следует изготовить предприятию, чтобы прибыль от их реализации была максимальной. Вариант 10. На производстве двух видов изделий A, B используется три различных вида сырья. Ресурсы сырья ограничены. Нормы затрат каждого из видов сырья на единицу продукции данного вида и цена единицы продукции каждого вида приведены в таблице: Вид сырья Нормы затрат сырья (кг) на единицу продукции Общее количество ресурса А В I 4 2 180 II 3 1 210 III 1 2 244 Цена единицы продукции (дол.) 10 14 Cоставить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной. Вариант 10. Молокоперерабатывающее предприятие производит пастеризованное молоко, кефир и сметану. О производстве известно следующее. Расход молочного сырья на производство каждого из трёх видов продукции – соответственно 1,01, 1,01 и 9,45 ц/ц. Фасовочные машины могут эксплуатироваться: автомат для молока и кефира – до 21 ч/сут. при производительности 5 ц/ч (молоко), 6 ц/час (кефир); автомат для сметаны – до 16 ч/сут. при производительности 0,3 ц/час. Технология не допускает выпуска менее чем 90 ц молока и 10 ц кефира и переработки более чем 140 ц молочного сырья в смену. Математическая формулировка задачи x1 – выпуск пастеризованного молока, ц/сут. x2 – выпуск кефира, ц/сут. x3 – выпуск сметаны, ц/сут. Баланс молока (сырья): 1,01x1 + 1,01x2 + 9,45x3≤140 (ц/сут.). Балансы оборудования: 0,2x1 + x2 / 6 ≤21 (ч/сут.), 10x3 / 3 ≤ 16 (ч/сут.) Минимальный выпуск продукции: x190 (ц/сут.), x210 (ц/сут.). Условия неотрицательности: x1 0, x2 0, x3 0 (ц/сут.). Максимум выручки: max 800x1 + 950x2 + 4200x3 (руб.). Вариант 11. [Химмельблау]. Максимизировать F(x1, x2) =3x1+5x2+4x3 при ограничениях 2x1+3x2≤8; 2x2+5x3≤10; 3x1+2x2+4x2≤15 для неотрицательных значений x1, x2, x3. Решение с использованием MS Excel Как было сказано на предыдущем занятии для решения задач оптимизации в Excel имеется пакет "Поиск решения". Приведём алгоритм решения задач линейного программирования в Excel. Шаг 1. Ввести условие задачи: 1. Создать экранную форму для ввода условия задачи (переменных, целевой функции, ограничений, граничных условий); 2. Ввести исходные данные в экранную форму (коэффициенты целевой функции, коэффициенты при переменных в ограничениях, правые части ограничений); 3. Ввести зависимости из математической модели в экранную форму (формулу для расчёта целевой функции, формулы для расчёта значений левых частей ограничений); 4. Задать целевую функцию (в окне "Поиск решения"): целевую ячейку, направление оптимизации целевой функции (min, max); 5. Ввести ограничения и граничные условия (в окне "Поиск решения"): ячейки со значениями переменных, граничные условия для допустимых значений переменных, соотношения между правыми и левыми частями ограничений. Шаг 2. Решить задачу: Установить параметры решения задачи (в окне "Поиск решения"); Запустить задачу на решение (в окне "Поиск решения"); Выбрать формат вывода решения (в окне "Результаты поиска решения"). Рассмотрим использования данного пакета для решения Задачи технического контроля. Можно сформулировать следующую задачу: минимизировать F(X)=40x1+36x2 при ограничениях: x1≤8, x2≤10, 5x1+3x2≥45, x1≥0, x2≥0. Рассмотрим алгоритм решения задачи: Шаг 1. Ввод данных: Создание экранной формы и ввод в неё условия задачи. Экранная форма для ввода условий задачи вместе с введёнными в неё данными представлена на рис. 1. Рис. 1. Экранная форма задачи Рис. 2. Экранная форма задачи после ввода всех необходимых формул Рис. 3. Окно "Поиск решения" для задачи технического контроля Рис. 4. Сообщение об успешном рении задачи и результаты решения Следовательно: x1opt=8, x2opt=1,67. Таким образом, при оптимальном режиме работы ОТК необходимо использовать восемь контролеров разряда 1 и 1.6 контролеров разряда 2. Дробное значение х2=1.6 соответствует использованию одного из контролеров разряда 2 в течение неполного рабочего дня. При недопустимости неполной загрузки контролеров дробное значение обычно округляют, получая приближенное оптимальное целочисленное решение х1opt=8, х2opt=2. Задания к ЗЛП Построение ОДР. Графическое решение. Решение с использованием MS Excel Вариант№1 Вариант№2 F(x)=-x1-2x2 → min F(x)=-3x1-2x2 → min x1+x2≥1 2x1-x2≥-1 x1-2x2≤0 x1≥0; x2≥0. x1+2x2≤7 2x1+x2≤8 x2≤3; x1≥0; x2≥0. Вариант№3 Вариант№4 F(x)=x1-2x2 → min F(x)=-x1-3x2 → min -x1+x2≤0 2x1+x2≤3 x1-x2≤1 x1≥0; x2≥0. 2x1+x2≤2 x1-x2≥0 x1-x2≤1 x1≥0; x2≥0. Вариант№5 Вариант№6 F(x)=-2x1-x2 → min F(x)=-x1-x2 → min 2x1+x2≥1 3x1-x2≥-1 x1-4x2≤2 x1≥0; x2≥0. x1≤3 x2≤2 x1+x2≤1 x2≥0; x1≥0. Вариант№7 Вариант№8 F(x)=-x1-4x2 → min F(x)=-x1-x2 → min x1≤2 x1+2x2≥2 x2≤2; x1+x2≤3 x1≥0; x2≥0. x1+x2≥1 x1-x2≥-1 x1-x2≤1; x1≤2; x2≤2 x1≥0; x2≥0. Вариант№9 Вариант№10 F(x)=-2x1-x2 → min F(x)=-x1-x2 → min x1+2x2≥2 2x2≥1 2x1-x2≥0 x1-2x2≤0; x1-x2≥-1 x1≥0; x2≥0. x1+x2≤3; x1≤2; x2≤2 2x1+x2≥2 x2≥0; x1≥0.