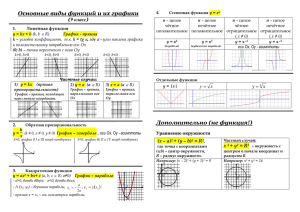
Образцы решения задач ОГЭ с параметрами по математике для
реклама
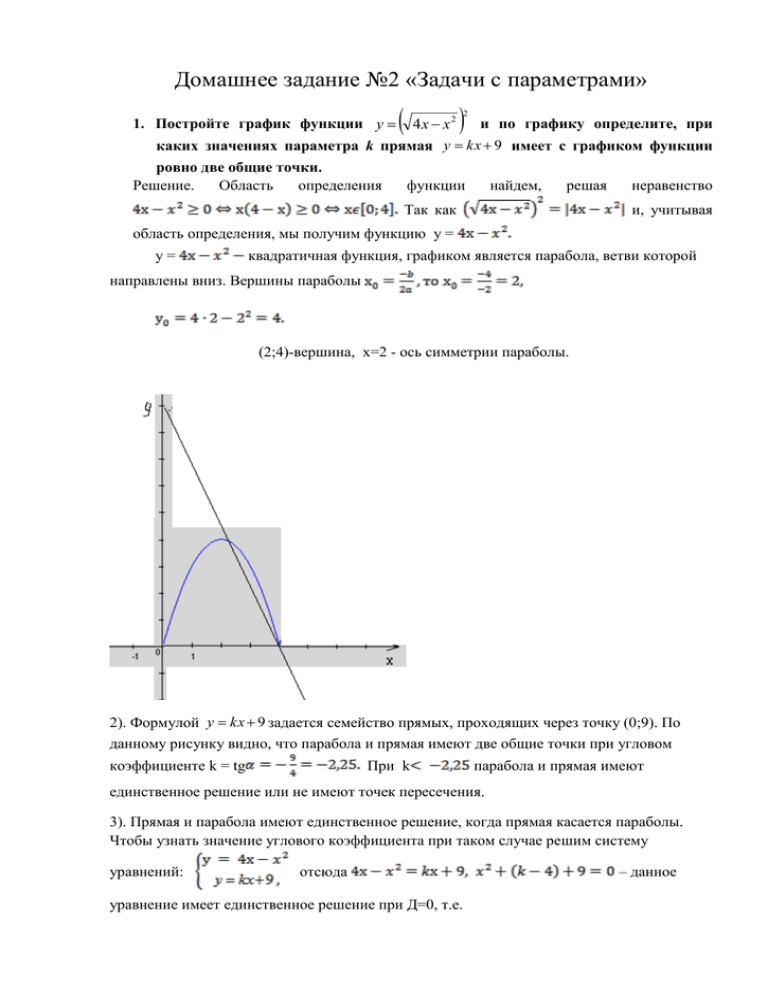
Домашнее задание №2 «Задачи с параметрами» 1. Постройте график функции y 4x x 2 2 и по графику определите, при каких значениях параметра k прямая y kx 9 имеет с графиком функции ровно две общие точки. Решение. Область определения функции найдем, решая Так как неравенство и, учитывая область определения, мы получим функцию у = у= квадратичная функция, графиком является парабола, ветви которой направлены вниз. Вершины параболы (2;4)-вершина, х=2 - ось симметрии параболы. 2). Формулой y kx 9 задается семейство прямых, проходящих через точку (0;9). По данному рисунку видно, что парабола и прямая имеют две общие точки при угловом коэффициенте k = tg При k парабола и прямая имеют единственное решение или не имеют точек пересечения. 3). Прямая и парабола имеют единственное решение, когда прямая касается параболы. Чтобы узнать значение углового коэффициента при таком случае решим систему уравнений: отсюда уравнение имеет единственное решение при Д=0, т.е. – данное Д= Решим уравнение k = 10, -2. При k = 10 прямая и парабола не имеют общих точек. Значит k = - 2. Ответ. Парабола и прямая имеют две общие точки при Пример 2. Постройте график функции y x x 2x2 2 x и по графику определите, x при каких значениях параметра d прямая y x d имеет с графиком функции ровно одну общую точку. Решение. 1). Если х то данная функция имеет вид квадратичная функция, ветви параболы направлены вниз. (2;4)-вершина, х=2 - ось симметрии параболы. 2). При х функция имеет вид у 3). Прямая y x d проходит через начало координат при d = 0, при остальных d семейство прямых, параллельных прямой у=х – биссектрисе первой и третьей координатной четверти. Прямая имеет с графиком функции ровно одну общую точку при но при d При d = 0 имеет две общие точки (прямая 2). Также имеет две общие точки, если прямая касается параболы . Решим систему уравнений Отсюда получим уравнение 9 - 4d=0, при d = D = 9 - 4d, прямая касается параболы. Значит при прямая и график функции имеют две общие точки. Ответ. прямая y x d имеет с графиком функции ровно одну общую точку при d иd Пример 3. Найдите все значения параметра a, при каждом из которых среди корней уравнения ax 2 a 4x a 1 0 имеется ровно один отрицательный корень. Решение. 1). При а=0 уравнение не имеет решения. 2). При а 0 возможны случаи: Условию задачи удовлетворяет только рисунок 1.Это возможно при выполнении условий: 3). При а Данная система не имеет решения. 0 возможны случаи: Условию задачи удовлетворяет только рисунок 1.Это возможно при выполнении условий Или Решим уравнение D= 16 + 4 Решением системы является промежуток Ответ. уравнение имеется ровно один отрицательный корень при