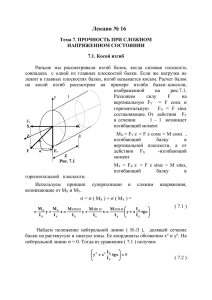
73-76

6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
6.1. Анализ структуры стержневых систем
Пусть N - степень статической неопределимости системы. Для систем
без замкнутых контуров ( рис. 6.1,а ) N=R - 3, где R - число реакций. Для
конструкций с замкнутыми контурами ( рис. 6.1,б ) N=3K-Ш, где K - число замкнутых контуров, Ш - число простых одиночных шарниров, таких,
которые соединяют в шарнире два элемента. При добавлении в шарнире
еще одного элемента, число Ш увеличивается на единицу.
I
C
II
X1
X3
B
a)
X2
а
Ш=2
III
Ш=1
б)
в)
б
Рис. 6.1
Так как статически неопределимую систему непосредственно
рассчитать не удается, превратим ее
г)
в статически определимую систему.
Основной системой называется статически определимая система, полуд)
ченная из статически неопределимой ( рис. 6.1,а ), отбрасыванием
Рис. 6.2
опорных связей ( рис. 6.2,а ), проведением разрезов ( рис. 6.2,б ), введением шарниров ( рис. 6.2,в ) или комбинацией этих способов.
Полученная основная система должна быть геометрически неизменяема, то есть ее элементы не должны перемещаться без их деформации. На
рис. 6.2,д изображена геометрически изменяемая основная система, полученная из статически неопределимой системы ( рис. 6.2,г ). Частным случаем геометрически изменяемой системы является мгновенно изменяемая
система ( рис. 6.2,е ).
Основная система, к которой приложена заданная нагрузка и неизвестные пока реакции отброшенных связей или внутренние силы называется эквивалентной системой.
73
8.2 Канонические уравнения метода сил
Введем обозначения:
 mn - перемещение по направлению mтой силы ( момента ) от nтой
нагрузки.
 mF - перемещение по направлению mтой силы ( момента ) от заданной нагрузки, называемое грузовым перемещением.
 mn - перемещение по направлению mтой единичной силы ( момента )
от nтой единичной нагрузки, называемое единичным перемещением.
 Amn – работа mтой силы ( момента ) на перемещении по ее направлению, вызванном nтой нагрузкой.
Выберем для расчета заданной системы ( рис.6.1,а ) эквивалентную
систему ( рис. 6.3 ). Найдем в эквивалентной системе вертикальное, горизонтальное и угловое перемещения точки C от заданной нагрузки. Вначале
найдем вертикальное перемещение 1F от заданной нагрузки. Затем
найдем вертикальное перемещение от силы X1. Приложим X 1  1 , от нее
перемещение равно 11, а от силы X1 будет 11X1.
Найдем вертикальное перемещение от силы X2. ПриC X2
ложим X 2  1, от нее перемещение равно 12: а от X2 буX1
дет 12X2. .Найдем вертикальное перемещение от силы
X3
X3. Приложим X 3  1 , от нее перемещение равно 13: а
B
от X3 будет 13X3. Используем принцип суперпозиции.
Рис. 6.3
Тогда полное вертикальное перемещение точки C запишется:
CВЕРТ  11  X1  12  X 2  13  X3  1F  0
Вертикальное перемещение точки C равно нулю, так как в заданной
конструкции имеются в этой точке опорные связи, и точка C вертикально
перемещаться не может. Аналогично найдем горизонтальное и угловое перемещения точки C:
CГОР   21  X1   22  X 2   23  X3   2 F  0 ,
C  31  X1  32  X2  33  X3  3F  0 .
Таким образом, получаем систему трех линейных алгебраических
уравнений относительно “ лишних “ неизвестных X1, X2 и X3, решая которую, найдем реакции в отброшенных связях рамы.
В общем случае для статически неопределимой системы со степенью
неопределимости, равной N, решается система канонических уравнений
метода сил N-ной степени.
74
11  X1  12  X 2  ...  1N  X N  1F  0
  X    X  ...    X    0
 21 1
22
2
2N
N
2F

                        

 N1  X1   N 2  X 2  ... NN  X N   NF  0
iк (
Коэффициенты ii называются главными i  k ) называются побочными iк >< 0.
( 6.1 )
ii > 0, коэффициенты
6.3. Теоремы о взаимности работ и взаимности перемещений
Теорема о взаимности работ
Рассмотрим
два состояния системы, различающихся порядком
нагружения. В первом состоянии ( рис. 6.4,а ) вначале приложим силу F!.
Работа силы F1 на перемещении 11 будет равна A11=0.5*F1*11. Затем к
системе приложим силу F2, тогда A22=0.5*F2*22 и A12=F1*12. Потенциальная энергия деформации системы равна сумме работ сил, и в первом
состоянии будет U1=A11+A22+A12 .
Во
втором
состоянии
( рис. 6.4,б ) изменим порядок нагружения. Вначале приложим силу F2.
F1
F2
Работа силы F2 на перемещении 22
I
будет равна A22=0.5*F2*22, Затем к
системе приложим силу F1, тогда
A11=0.5*F1*11 , A21=F2*21. Потенци11
11
альная энергия деформации системы
12
F1
F2
во втором состоянии будет
U2=
II
A11+A22+A21. Так как потенциальная
энергия деформации системы не зависит от порядка нагружения, а зави11
11
сит от конечного состояния кон12
струкции, то A12=A21.
Рис. 6.4
В общем случае
Aik = Aki ..
Теорема о взаимности перемещений
Если
Fi = 1,
Fk = 1 ,
то Fi*ik
= Fk*ki
и
ik = ki.
75
6.4. Порядок расчета статически неопределимых систем методом сил
1. Находим степень статической неопределимости системы по формулам
N=R – 3 или N=3K-Ш.
2. Записываем систему канонических уравнений метода сил ( 6.1 ) для
найденного значения N.
3. Рассматриваем один или
несколько вариантов основных систем
и соответствующих им эквивалентных систем и выбираем для дальнейшего расчета наиболее простой вариант эквивалентной системы.
4. Находим единичные коэффициенты,
входящие в канонические
уравнения метода сил. Для этого к выбранной основной системе прикладываем поочередно единичные « лишние » неизвестные, находим от
их действия единичные внутренние усилия в элементах основной
системы и используем интегралы Мора. Для применения способа Симпсона строем эпюры единичных внутренних усилий.
5. Определяем грузовые коэффициенты, входящие в канонические уравнения метода сил. Для этого к выбранной основной системе прикладываем
внешнюю нагрузку, находим от ее действия грузовые внутренние усилия в элементах основной системы и используем интегралы Мора.
Для применения способа Симпсона строем эпюры грузовых внутренних
усилий.
6. Подставляем найденные единичные и грузовые коэффициенты в систему канонических уравнений метода сил, решаем ее и находим значения « лишних » неизвестных.
7. Рассматриваем выбранную эквивалентную систему с найденными значениями « лишних » неизвестных.
8. Находим внутренние усилия в элементах выбранной эквивалентной
системы и строим их эпюры.
9. Проводим статическую проверку равновесия узлов конструкции
и кинематическую проверку – вычисляем перемещения выбранной
эквивалентной системы по
направлению отброшенных связей. Эти
перемещения должны отсутствовать.
10.Проводим проверку элементов статически неопределимой конструкции
на прочность.
76