4. Вопрос №4

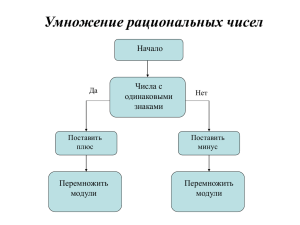
4. Действия с рациональными числами.
Модулем числа 𝑎 называют расстояние (в единичных отрезках) от начала координат до точки
A(a).
Модуль не может быть отрицательным.
Модуль положительного числа равно самому числу.
Модуль отрицательного числа равен противоположному числу.
Противоположные числа имеют равные модули. Модуль числа ноль(0) равен нулю.
|0| = 0;
|1,5| = 1,5
|−3| = 3
a, если a положительное число
|𝑎| =
- a, если a отрицательное число
Сравнение чисел.
Любое отрицательное меньше любого положительного числа.
Нуль больше любого отрицательного числа, но меньше любого положительного числа.
Из двух отрицательных чисел меньше то, модуль у которого больше.
Сложение отрицательных чисел.
Чтобы сложить два отрицательных числа нужно:
1) Сложить их модули;
2) Поставить перед полученным числом знак минус.
Сложение чисел с разными знаками.
Чтобы сложить два числа с разными знаками надо из большего модуля вычесть меньший и
перед полученным результатом поставить знак большего модуля.
Сумма противоположных чисел равна нулю: 9 + (- 9) = 0
Свойства нуля:
0+3=3;
-4+0=-4;
0+(-7)=-7
Вычитание.
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число,
противоположное вычитаемому.
Умножение.
Чтобы перемножить 2 числа с разными знаками, надо перемножить модули этих чисел и
поставить перед полученным числом знак минус.
Чтобы перемножить 2 отрицательных числа, надо перемножить модули этих чисел.
Если количество отрицательных чисел чётно, то результат положительный:
-1•(-1)•(-1)•(-1) =1
Если количество отрицательных чисел нечётно, то результат отрицательный:
-1•(-1)•(-1)•(-1)•(-1) = -1
Деление.
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на
модуль делителя.
При деление чисел с разными знаками надо:
1) Разделить модуль делимого на модуль делителя;
2) Поставить перед полученным числом знак минус.
Свойства нуля и единицы.
5∙1=5; -3∙1= -3;
5:1=5; -3:1= -3;
a∙1=a
a:1=a
8∙0=0;
-7∙0=0
a∙0=0
делить на «0» нельзя
Раскрытие скобок перед которыми стоит знак «-» и «+».
Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки
слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его
записать со знаком «+».
Чтобы раскрыть скобки перед которыми стоит знак «-», надо заменить этот знак на «+», поменяв
знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Раскрытие скобок перед которыми стоит знак умножения: a∙(b±c)=ab±ac
Чтобы число умножить на сумму (разность), нужно число умножить на первое слагаемое, затем
на второе слагаемое и произведения сложить (вычесть).
Подобные слагаемые.
Слагаемые, имеющие одинаковую буквенную часть, называются подобными слагаемыми.
Чтобы привести подобные слагаемые надо сложить их коэффициенты и результат умножить на
общую буквенную часть 5a + a - 2a = 4a.
Уметь решать уравнения, применяя свойства:
1) Корни уравнения не изменяются, если обе части уравнения умножить или разделить на
одно и то же число, не равное нулю.
2) Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части
уравнения в другую, изменив при этом знак на противоположный.
Все уравнения мы приводим к виду ax = b, где a ≠ 0. Уравнение, которое можно привести к такому
виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным
уравнением с одним неизвестным.