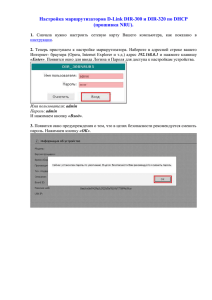
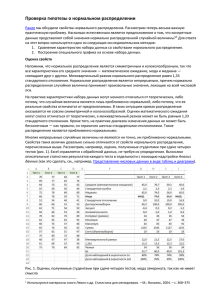
Рис.1. График плотности нормального распределения N(0,1) Рис
реклама

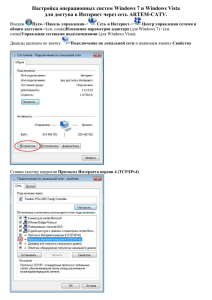
0,45 0,4 0,35 0,3 0,25 Ряд1 0,2 0,15 0,1 0,05 5 4,6 4,2 3,8 3,4 3 2,6 2,2 1,8 1,4 1 0,6 0,2 -0,2 -0,6 -1 -1,4 -1,8 -2,2 -2,6 -3 -3,4 -3,8 -4,2 -4,6 -5 0 Рис.1. График плотности нормального распределения N(0,1) 1,2 1 0,8 0,6 Ряд1 0,4 0,2 Рис.2. График функции нормального распределения N(0,1) Графики построены средствами Excel 2010 5 4,6 4,2 3,8 3,4 3 2,6 2,2 1,8 1,4 1 0,6 0,2 -0,2 -0,6 -1 -1,4 -1,8 -2,2 -2,6 -3 -3,4 -3,8 -4,2 -4,6 -5 0 Построение функции распределения для нормального распределения с мат.ожиданием m и дисперсией d2 в программе Excel 2010. Пример построен для m=3, d2=1,5 (d1,23) 1) находим интервал (m-4d; m+4d) (-3;9) (интервал можно увеличить, чтобы его концы имели целые значения). В клетке А1 ставим левый конец интервала, в клетке А2 ставим левый конец+ 0,5 или +0,2 (какой шаг хотите получить на графике). Выделяем клетки А1 и А2, тянем вниз за правый угол, пока не дойдем до значения, равного правому концу интервала. 2) В клетку В1 ставим: Формулы - другие функции – статистические – НОРМ.РАСП В аргументы функции НОРМ.РАСП указываем: Х-число А1, среднее – число m, Стандарт_откл – число d, Интегральная – ИСТИНА (если ЛОЖЬ – получим плотность распределения) (см. рис.3) Нажимаем ОК Рис.3. Первая часть построения функции распределения. 3) Тянем за правый угол клетки В1 до конца заполненных клеток в столбце А. Получили значения функции нормального распределения, которые осталось изобразить на графике. 4) Вставить – график - выбрать данные – выбираем столбец В с заполненными клетками. Строим график. 5) Чтобы по горизонтали шли значения из столбца А, при выделенном окне графика жмем правую кнопку мыши, нажимаем выбрать данные – подпись горизонтальной оси – изменить – выделяем столбец А с заполненными клетками. Теперь построенный график можно скопировать в PowerPoint или Paint и на нем достроить график дискретного биномиального распределения с такими же ожиданием m=np и дисперсией d2= np(1-p). Посмотрите, будут ли похожи эти графики.