Добавить в коллекции Добавить в сохраненное
  1. Без категории

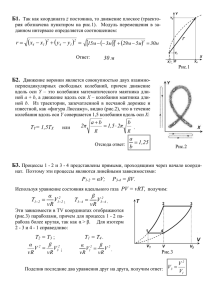
Алиев Р.А. Обратная задача определения коэффициента в

реклама
реклама
Каталог карточек
Похожие документы
N - Научная библиотека Томского государственного университета
N - Научная библиотека Томского государственного университета
Задачи по олимпиаде 8 класс
Задачи по олимпиаде 8 класс
О ПРИБЛИЖЕНИИ ВЫПУКЛЫХ ФУНКЦИЙ РАЦИОНАЛЬНЫМИ
О ПРИБЛИЖЕНИИ ВЫПУКЛЫХ ФУНКЦИЙ РАЦИОНАЛЬНЫМИ
Задача 251
Задача 251
XI Международная дистанционная олимпиада «Эрудит» Математика 9 класс 2 тур
XI Международная дистанционная олимпиада «Эрудит» Математика 9 класс 2 тур
решения заданий Олимпиады по физике
решения заданий Олимпиады по физике
Замов Наиль Калимович
Замов Наиль Калимович
Скачать
реклама