АЛГОРИТМ ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ © Горелова А.В. , Любимова Т.В.

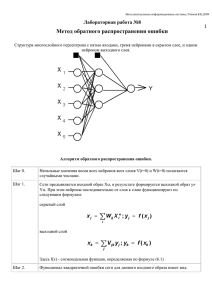
Технические науки
151
АЛГОРИТМ ОБРАТНОГО РАСПРОСТРАНЕНИЯ
ОШИБКИ
© Горелова А.В., Любимова Т.В.
Северо-Кавказский филиал Белгородского государственного
технологического университета им. В.Г. Шухова, г. Минеральные Воды
В данной статье мы рассмотрим алгоритм обратного распространения ошибки. Начнем с того что же такое нейронная сеть. Для простоты
объяснения этого понятия можно рассмотреть нейронную сеть в качестве взвешенного направленного графа, узлы (нейроны) которого расположены слоями. Узел одного слоя имеет связи со всеми узлами предыдущего слоя. При этом присутствуют входной и выходной слои, узлы которых выполняют роль входов и выходов соответственно. Каждый из узлов (нейрон) обладает активационной функцией которая ответственна за вычисление сигнала на выходе узла (нейрона). По мимо
этого имеется понятие смещения. Смещение это узел, на выходе которого всегда появляется единица.
Ключевые слова: алгоритм обратного распространения ошибки,
нейронная сеть, графы, многослойный персептрон.
Существует два типа обучения нейронных сетей – с учителем и без учителя. В случае с учителем, на входной вектор имеется готовый ответ, в случае без учителя нейронная сеть самообучается. У каждого типа обучения
есть свои задачи и они почти не пересекаются. На сегодняшний день придумано множество архитектур нейронных сетей и методов их обучения. Но
основными являются – для обучения с учителем это «алгоритм обратного
распространения ошибки», а для обучения без учителя это алгоритмы Хебба и Кохонена. Эти типы очень схожи с биологической реальностью, например – ребенок обучается с учителем или без? Что то ребенку показывают родители и учителя, чему то он учиться сам. Есть так же половинчатые
примеры обучения, например игра в мяч во дворе, малыш видит как это получается у других и сам процесс обучения он проходит самостоятельно [1].
Для того чтобы решить задачи с помощью нейронных сетей необходимо:
1. Подробно рассмотреть поставленную задачу и проанализировав еѐ
подумать не легче ли будет решить еѐ при помощи других методов;
2. Определить множество входов. Множество входов выбирается в
течении некоторого времени и отбираются те на которых выдается
наименьшая ошибка;
3. Необходимо выбрать выходные переменные, то есть то что будет на
выходе нейронной сети;


Преподаватель кафедры «Экономических и естественно-научных дисциплин».
Старший преподаватель кафедры «Экономических и естественно-научных дисциплин».
152
НАУКА И СОВРЕМЕННОСТЬ – 2015
4. Определить какое будет количество слоев и узлов в них;
5. Сгенерировать сеть и обучить ее на данных примерах.
Алгоритм обратного распространения ошибки это один из методов обучения многослойных нейронных сетей прямого распространения, которых
ещѐ называют многослойными персептронами. Многослойные персептроны часто применяются для решения многих сложных задач [2].
Предполагается два подхода по всем слоям сети для обучению алгоритма обратного распространения ошибки: прямой и обратный. При прямом
проходе входной вектор подается на входной слой нейронной сети, после
чего разделяется по сети от слоя к слою. В процессе производиться набор
выходных сигналов которые являются действительной реакцией сети на
имеющийся входной образ. Во время прямого прохода все синаптические
веса сети фиксированы, а при обратном проходе все синаптические веса
настраиваются в соответствии с правилом коррекции ошибок. Фактический
выход сети выводиться из желаемого, в результате этого формируется сигнал ошибки. Этот сигнал после распространяется по сети в направлении,
обратном направлению синаптических связей. Отсюда и название алгоритм
обратного распространения ошибки. Синаптические веса настраиваются с
целью лучшего приближения выходного сигнала сети к желаемому.
Рассмотрим подробнее работу алгоритма. Представим, нужно обучить
следующую нейронную сеть, используя алгоритм обратного распространения ошибки (рис. 1).
Рис. 1. Пример двухслойного персептрона
Технические науки
153
На приведенном рисунке применяются следующие условные обозначения:
‒ каждому слою нейронной сети соответствует своя буква;
‒ все нейроны каждого слоя пронумерованы арабскими цифрами;
‒ WA1-B1 – синаптический вес между нейронами A1 и B1;
‒ OUTA1 – выход нейрона A1.
В качестве активационной функции в многослойных персептронах обычно используется сигмоидальная активационная функция, в частности логистическая:
OUT =
1
,
1  exp(Y )
где α – параметр наклона сигмоидальной функции (рисунок 2). Изменяя
этот параметр, можно построить функции с различной сложностью. В дальнейшем будут использованы только логические функции активации.
Рис. 2. График функции в многослойном персептроне
Сигмоид уменьшает диапазон изменения так, что значение OUT лежит
между нулем и единицей. Если имеются нелинейности то многослойные нейронные сети буду обладать большей мощностью чем однослойные. Требуемую
нелинейность будет давать сжимающая функция. Имеется множество функций, которые можно использовать. Для алгоритма обратного распространения
ошибки необходимо только, чтобы функция была везде дифференцируема.
Сигмоид подходит этому требованию. Ещѐ одно его преимущество состоит в
автоматическом контроле усиления. Для слабых сигналов (т.е. когда OUT близко к нулю) кривая вход-выход имеет сильный наклон, который дает большое
усиление. Усиление будет падать, когда величина сигнала увеличивается. Из
вышесказанного следует, что большие сигналы воспринимаются сетью без
насыщения, а слабые сигналы проходят по сети без особого ослабления [3].
Подстановка весов алгоритма обратного распространения ошибки так,
чтобы приложение некоторого множества входов приводило к требуемому
154
НАУКА И СОВРЕМЕННОСТЬ – 2015
множеству выходов является целью обучения. Для простоты эти множества
входов и выходов можно называть векторами. При обучении ожидается, что
для каждого входного вектора существует парный ему целевой вектор, который задает необходимый выход. В общем они называются обучающей
парой. Сеть обучается на множестве пар.
Рассмотрим корректировку весов сети. Здесь следует выделить два приведенных ниже случая.
Случай 1. Корректировка синаптических весов выходного слоя.
Например, для модели нейронной сети на рис. 1, это будут веса имеющие следующие обозначения: WB1-C1 и WB2-C1. Обозначим, что индексом p
будем обозначать нейрон, из которого выходит синаптический вес, а q – нейрон в который входит:
Рис. 3. Корректировка синаптических весов выходного слоя
Вводим величину δ, которая равна разности между требуемым Tq и реальным OUTq выходами, умноженной на производную логистической функции активации:
 q  OUTq (1  OUTq )(Tq  OUTq ).
Тогда, веса выходного слоя после коррекции будут равны:
Wp q (i  1)  Wp q (i)   qOUTp ,
где i – номер текущей итерации обучения;
Wp-q – величина синаптического веса, соединяющего нейрон p с нейроном q;
η – коэффициент «скорости обучения», позволяет управлять средней величиной изменения весов;
OUTp – выход нейрона p.
Приведем пример вычислений для синаптического веса WB1-C1:
 C1  OUTC1 (1  OUTC1 )(T1  OUTC1 )
WB1C1 (i  1)  WB1C1 (i)   OUTB1
C1
Технические науки
155
Случай 2. Корректировка синаптических весов скрытого слоя.
Для модели нейронной сети на рис. 1, это будут веса соответствующие
слоям A и B. Определим, что индексом p будем обозначать нейрон из которого выходит синаптический вес, а q – нейрон в который входит (обратите
внимание на появление новой переменной k):
Рис. 4. Корректировка синаптических весов скрытого слоя
Вводим величину δ, которая равна:
M
 q  OUTq (1  OUTq )  k wq k ,
k 1
N
где

– сумма от 1 по N.
k 1
Тогда, веса скрытых слоев после коррекции будут равны:
W p q (i  1)  W p q (i)   q OUTp
Приведем пример вычислений для синаптического веса WA1-B1:
 B1  OUTB1 (1  OUTB1 )
WA1 B1 (i  1)  WA1 B1 (i)   B1OUTA1
Для каждого нейрона в скрытом слое должно быть вычислено δ и подстроены все веса, ассоциированные с этим слоем. Процесс будет повторяться слой за слоем по направлению к входу, до тех пор, пока все веса не будут
подкорректированы [3].
156
НАУКА И СОВРЕМЕННОСТЬ – 2015
Появление алгоритма обратного распространения ошибки стало важным
событием в области развития нейронных сетей, поскольку он реализует вычислительно эффективный метод обучения многослойного персептрона. Конечно неверно утверждать, что алгоритм обратного распространения ошибки
дает действительно оптимальное решение всех потенциально решаемых проблем, но он дал надежду относительно обучения многослойных машин.
Список литературы:
1. Головачев А.Г. Лекции по курсу «Нейросетевые технологии». – 2008.
2. Уоссермен Ф.Нейрокомпьютерная техника. Теория и практика. – 1992.
3. Нейронные сети: алгоритм обратного распространения [Электронный
ресурс] / С. Короткий. – Режим доступа: http://www.uran.donetsk.ua.
КОМПАКТНОЕ СИММЕТРИРУЮЩЕЕ УСТРОЙСТВО
НА ТРЕХ СВЯЗАННЫХ ЛИНИЯХ ПЕРЕДАЧИ1
© Девятков Г.Н., Протасова М.В.
Новосибирский государственный технический университет, г. Новосибирск
В данной статье рассмотрено компактное согласующее-симметрирующее устройство на связанных линиях передачи, получена его математическая модель, найдены условия идентичности передачи сигнала в
плечи. В качестве примера проведен синтез и моделирование компактного согласующе-симметрирующего устройства в полосе нормированных рабочих частот 0,7-1,3 с модулем коэффициента отражения по
входу не более 0,2 для различных сопротивлений нагрузок.
Ключевые слова: компактное симметрирующее устройство, согласование, связанные отрезки линий передачи.
Введение
Симметрирующие устройства – это основные компоненты во многих
коммуникационных устройствах, таких как балансный смеситель, двухтактный усилитель, антенные системы и др. Основные функции симметрирующего устройства – это симметрирование и согласование. Важнейшими характеристиками симметрирующего устройства являются широкополосность, уровень модуля коэффициента отражения в полосе пропускания. Одной из современных тенденций развития симметрирующих устройств является миниатюризация конструкции данных устройств.
Работа выполнена при финансовой поддержке Минобрнауки России (Госзадание № 8 337 2014/К).
Профессор кафедры Конструирования и технологии радиоэлектронных средств, доктор
технических наук, доцент.

Аспирант кафедры Конструирования и технологии радиоэлектронных средств.
1
