Модели ядерных реакций. Составное ядро. Задачи.

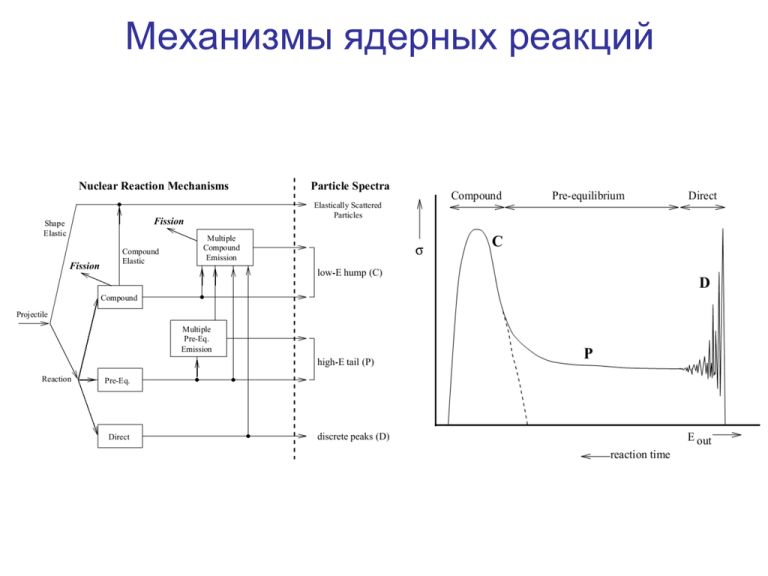
Механизмы ядерных реакций
Механизмы ядерных реакций. Составное ядро.
Согласно этой модели ядерная реакция протекает проходит в две стадии. На
первой частица a и ядро мишень А образуют связанную систему составное
(компаунд) ядро С, которое на второй стадии распадается на ядро В и
частицу b:
a AC  Bb
 ab   aC Pb
 aC  сечение образования составного ядра,
Pb  вероятность распада составного ядра по каналу b  B.
Вероятность распада по данному каналу определяется
конкуренцией различных, открытых при данной энергии,
каналов реакций i с шириной i:
Pb 
b
,  Pi  1
 i i
i
Механизмы ядерных реакций. Составное ядро.
Применимость предположения Бора связана с большим числом
перераспределений энергии в составном ядре. Для этого длина
свободного пробега падающей частицы в ядре должна быть меньше
радиуса ядра.

1
0
  сечение взаимодействия частицы с одним нуклоном
0  плотность нуклонов в ядре
При энергиях нейтронов En сечение зависит от энергии
относительного движения нейтрона и нуклона E  1 ( E0  En )
2
4 МэВ
 [барн] 
E
[см]  0.9 1015 ( E0  En )[МэВ]
Механизмы ядерных реакций. Составное ядро.
Условия применимости предположения Бора:

En
Rя
ABn ( Bn  энергия отделения нейтрона
от составного ядра)
При A  10, En  50МэВ
Время жизни составного ядра.
Сечение взаимодействия нейтронов с 238U
  0.1эВ    1014 c
Время жизни составного ядра.
За счет каких причин составное ядро является долгоживущим?
- Энергия возбуждения составного ядра меньше полной энергии связи.
- Радиационные распады (n,g) – электромагнитные t=10^-14 c
- Кулоновский барьер для заряженных частиц
- Правила отбора
Проверка гипотезы составного ядра.
a AC  Bb
 ab   aC Pb
b
Pb 
, где  i   a   b   b '  ...
i
 i
i
 , , ,
i
a
b
b'
 не зависят
i
от входного канала
b ' B '  C  B  b  b 'b   b 'C Pb

 ab  bb

 ab '  bb '
Механизмы ядерных реакций
Уровни промежуточного ядра
E *C  E *нач  Ba  Ea
Ea  энергия относительного
движения a и A
Сечение образования составного ядра
Проникновение нейтрона через поверхность ядра
d 2 ( x)  2m
l (l  1) 
  2 ( E  V ( x)) 
 ( x)  0
2
2
dx
x 

  exp(ik0 x)   exp(ik0 x), x  R
   exp(ikx), x  R
 ,   амплитуда отраженной и прошедшей волны
k
2mE
, k0 
2m( E  V0 )
|  |2 коэффициент отражения
p  1 |  |2 коэффициент прохождения
Из условия непрерывности  и ее производной
( k0  k )
1+   и (1   )k0   k   
( k0  k )
 p  1 |  |2 
4 k0 k
( k0  k ) 2
Проникновение нейтрона через поверхность ядра
При низких En , k
 p  1 |  |2 
k0
4 k0 k
En
4k


4
( k0  k ) 2 k0
( En  V0 )
n  p
1

В случае гармонического осциллятора будут эквидистантные уровни с
энергией E  (расстояние между уровнями),
2
при этом  


n  
   непрерывный спектр
 2
n  p


,  p
  квазидискретный спектр
 n , 
n
Дисперсионный характер сечения
Сечение взаимодействия нейтронов с 238U
Сечение в области изолированных резонансов
R/
   (2l  1) 2l
l 0
При T  1кэВ,
R  l  0
0 p  n из-за отражения
0

 (W )
 дисперсионный характер сечения
(W  W0 )  ( )
2
 n
2
 
(W  W0 ) 2  ( ) 2
2
Через кинетические энергии T  W  Bn
 
2
2
 n
(T  T0 ) 2  ( ) 2
2
2
Формулы Брейта-Вигнера для бесспиновой
частицы с l=0
a AC  Bb
 a b
2
 ab  
(W  W0 ) 2  ( ) 2
2
b
a
b
2
 ab   aC Pb   aC


(W  W0 ) 2  ( ) 2 
2
 длина волны,W  Ba  Ta , Ta  энергия налетающей частицы,
Ba  энергия связи частицы a в ядре C ,
W0  энергия уровня составного ядра, Г  полная ширина уровня,
Г a и Г b  парциальные ширины уровня,
отвечающие испусканию частиц a и b из составного ядра.
Формулы Брейта-Вигнера для частицы с l=0
 a b
2J  1
 ab  
(W  W0 ) 2  ( ) 2 (2 I  1)(2 s  1)
2
s  спин налетающей частицы
I  спин мишени
J  спин составного ядра
2
Сечение резонансного и потенциального рассеяния
нейтронов
В области резонансов
 nn  
2
 2n
 n (W  W0 )
 4 R  4 R
2
2
(W  W0 )  ( )
(W  W0 ) 2  ( ) 2
2
2
2
Сечение резонансного рассеяния и захвата нейтронов
Сечения образования составного ядра нейтронами при малых энергиях
в области ниже первого резонанса
 aC  
k
2
2mE
p
4
 2
k0 k
, k0 
2
1
EV0
2m( E  V0 )
1
v
, v  скорость нейтрона
Сечение резонансного рассеяния и радиационного захвата
нейтронов
2

2J  1
2
n
 nn  
(W  W0 ) 2  ( ) 2 (2 I  1)(2 s  1)
2
 n 
2J  1
2
 n  
(W  W0 ) 2  ( ) 2 (2 I  1)(2 s  1)
2
В области ниже резонансов W W0

const
n
4k
p
k0
n
v
     n     , но
  n
1
v
1
2
1
v2
В области первых резонансов

2J  1
W  W0   n (W0 )   2 n 2
( ) (2 I  1)(2 s  1)
2
4 2  n
2J  1
при     n (W0 ) 

(2 I  1)(2 s  1)
Сечение резонансного рассеяния и радиационного захвата
нейтронов
с ростом Tn и W , растет  n
4k
p
k0
v
сечение резонансного рассеяния нейтронов
становится доминирующим  n 
Сечение в нерезонансной области
Сечение в нерезонансной области
(неупругое рассеяние)
R/
R/
 н. р.   Sll   l (l  1)
l 0
l 0
R/
2
p   l (l  1)
l 0
4 k0 k
  (R  )
( k0  k ) 2
2
для быстрых нейтронов
R, k  k0
4k0 k
  ( R  )   R ,
1
2
( k0  k )
2
2
    R 2 ( монотонно убывает)
2
4 k0 k

2
( k0  k )
Дифракционное рассеяние

2


(
R

)
, при
д. р .
 
(
R
2


R
д. р .
R)   д. р. 
2

2

R
н. р .
Ограничение модели составного ядра
Зависимость полного сечения взаимодействия нейтронов с различными
ядрами от энергии нейтронов. Сплошные линии - эксперимент, штриховые
линии - предсказания модели "черного ядра"
  2 R
2
Задачи
1. Оценить сечение реакции 63Cu(p,n)63Zn, если известны сечения
реакций, идущих с образованием того же составного ядра с той же
энергией возбуждения: 60Ni(α,p)63Zn - 0.7 б; 63Cu(p,pn)62Cu - 0.87 б;
60Ni(α,pn)62Cu - 0.97 б.
2. Оценить нейтронную ширину Гn изолированного уровня 0+ ядра
108Rh (энергия уровня E = 1.21 эВ, полная ширина Г = 0.21 эВ), если
0
при резонансном поглощении нейтронов с образованием этого
уровня составного ядра сечение поглощения для энергии нейтронов
Tn = 1 эВ σ = 2700 б. Спин ядра-мишени I(107Rh) = 1/2.