опд.02. техническая механика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
ГБОУ СПО МО Ореховский индустриальный техникум
специальность 08.02.01. Строительство и эксплуатация зданий и
сооружений
ОПД.02. ТЕХНИЧЕСКАЯ
МЕХАНИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ
НА РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ.
Преподаватель
г.о. Орехово-Зуево
2013
Фомин С.А.
Содержание
1. Пояснительная записка
2. РГР №1. Подобрать сечение стержня по данным одного из
вариантов. Материал стержня для фасонных профилей -прокатная
сталь С-245
3. РГР № 2. Для балки с нормативной нагрузкой построить эпюры Q и М
и подобрать сечения из двутавра. Построить эпюры касательных и
нормальных напряжений, в которых Q мах и М мах
4. РГР №3. Построить эпюры Nx, Qx, Mx для статически определимой
рамы.
5. РГР №4. Определить усилия в стержнях фермы от полной расчетной
нагрузки путем построения диаграммы Максвелла-Кремоны. Провести
анализ усилий в поясах
6. РГР №5. Расчет неразрезных балок с помощью таблиц.
Построение эпюр M 0, M or, M∑.
7. Оформление работ
8. Литература
2
Пояснительная записка
Данное пособие содержит методические указания по выполнению расчетнографических работ по дисциплине ОПД.02. ТЕХНИЧЕСКАЯ МЕХАНИКА для
специальности
08.02.01. Строительство и эксплуатация зданий и
сооружений.
В документе содержатся:
 Расчетно-графические работы по изучаемым разделам
дисциплины. Для каждой работы прописаны: тема; цель; общие положения;
пример выполнения задания и непосредственно задание
 пример оформления расчетно-графической работы
 список литературы
При необходимости каждый студент может воспользоваться
методическими указаниями для подготовки к практической работе, её
выполнению и оформлению.
В рабочей программе «Техническая механика» предусмотрен вид
учебной работы - самостоятельная работа обучающегося, который
предусматривает выполнения расчётно-графических работ в объеме 30
часов:
Самостоятельная работа по разделу 2
Выполнение РГР №1
Подобрать сечение стержня по данным одного из вариантов. Материал
стержня для фасонных профилей - прокатная сталь С-245
Выполнение РГР № 2.
Для балки с нормативной нагрузкой построить эпюры Q и М и подобрать
сечения из двутавра. Построить эпюры
касательных и нормальных
напряжений, в которых Q мах и М мах
Самостоятельная работа по разделу 3.
Выполнения РГР №3 Построить эпюры Nx, Qx, Mx для статически
определимой рамы.
Выполнения РГР №4 Определить усилия в стержнях фермы от полной
расчетной нагрузки путем построения диаграммы Максвелла-Кремоны.
Провести анализ усилий в поясах
Выполнения РГР №5 Расчет неразрезных балок с помощью таблиц.
Построение эпюр M 0, M or, M∑.
Все задачи составлены по многовариантной системе.
При выполнении работы необходимо соблюдать следующие требования:
- записывается условия задач;
- решения задач следует сопровождать пояснениями;
- вычислениям должны предшествовать исходные формулы;
- для всех исходных и вычисленных физических величин, должны
указываться размерности;
3
- приводятся необходимые эскизы, схемы.
На каждой странице оставляются поля шириной 3—4 см для замечаний
проверяющего работу. За ответом оставляется место для рецензии.
На титульном листе разборчиво пишутся наименование учебного
заведения, специальность, наименование учебной дисциплины, номер варианта;
фамилия, имя, отчество учащегося; группа.
Приводим образец заполнения обложки:
Государственное бюджетное образовательное учреждение среднего
профессионального образования Московской области Ореховский
индустриальный техникум
Специальность 08.02.01 «Строительство и эксплуатация зданий и
сооружений»
Техническая механика
Расчетно-графическая работа №
Петров Виктор Александрович
Группа С-21
В установленные учебным графиком сроки студент направляет
выполненную работу для проверки преподавателю.
После получения прорецензированной работы студенту необходимо
исправить отмеченные ошибки, выполнить все указания преподавателя,
повторить недостаточно усвоенный материал.
Не зачтенные расчетно-графические работы подлежат повторному выполнению.
Задания, выполненные не по своему варианту, не засчитываются и
возвращаются студенту.
Расчетно-графические работы оцениваются по пятибалльной системе
с учетом следующих требований и пороговых показателей:
Оценка «5» - ответы на вопросы при защите даны в полном объеме, все
задачи решены верно.
Оценка «4» - ответы на вопросы при защите даны в полном объеме, все
задачи решены верно, но допущены неточности или
несущественные ошибки при оформлении документов.
Оценка «3» - ответы на вопросы при защите даны, все задачи решены, но
допущены существенные ошибки и неточности.
Оценка «2» - ответы на вопросы при защите не даны, задачи не решены.
.
В методических указаниях приведены примеры решения задач.
4
РАЗДЕЛ 2
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Расчетно-графическая работа №1
Тема . Осевое растяжение и сжатие.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Подбор сечений стержней из расчета на прочность.
1. Мысленно отбрасывают связи и заменяют их действие на брус
реакциями. В задачах для самостоятельной работы абсолютно жесткий брус
удерживается в равновесии шарнирно-неподвижной опорой и одиночным
стержнем (подвеской или колонной).
По условию задачи требуется рассчитать только стержень, поэтому
рекомендуется показать усилие в стержне N и не показывать реакций опоры,
определение которых выходит за рамки самостоятельной работы.
Направление неизвестного усилия можно принять произвольно, но можно
руководствоваться и более конкретной рекомендацией: усилие направлено
по оси стержня в сторону, противоположную действию нагрузки.
Приведенные схемы нагрузок дают возможность безошибочно определить
направление действия усилия.
2. Определяют величину усилия N в стержне. Для этого составляют всего
одно уравнение равновесия — сумма моментов всех сил относительно
неподвижной опоры должна быть равна нулю: ∑МА{В) = 0. Неподвижная
опора в одних заданиях может быть обозначена А, в других — В.
Проверка решения не выполняется, так как не определялись опорные
реакции неподвижной опоры.
3. Определяют требуемую площадь поперечного сечения стержня из
условия прочности по формуле
АТр ≥ N/ R ,
(а)
где N — усилие в стержне; R — расчетное сопротивление материала
подвески по прил. VIII.
Следует обратить внимание на то, что в отличие от СНиПа, в расчетной
формуле коэффициент условия работы ус принят равным 1 и исключен из
знаменателя, а также вместо Ry принято R.
Это сделано из-за отсутствия сведений о назначении элементов стальных
конструкций и для получения единообразных формул при расчете
конструкций из разных материалов (стали прокатной фасонной, стали
арматурной, алюминия).
Подбор сечения сжатого стержня предлагается выполнить только из
расчета на прочность без учета потери устойчивости.
При пользовании формулой (а) следует помнить, что усилие N имеет
размерность кН, расчетное сопротивление R — МПа, а требуемую площадь
АТР измеряют в см2 для удобства пользования прил. I, поэтому необходимы
преобразования в размерностях. Они будут показаны в примере.
4. По найденной площади определяют требуемый профиль прокатной
стали или диаметр арматурного стержня согласно заданию.
5
Требуемый профиль прокатной стали определяют по площади АТР,
используя прил. I, а диаметр стержня можно найти по формуле
d T Р = √4 АТР /π.
(б)
При назначении диаметра стержня полученный результат в формуле (б)
рекомендуется округлить до размера, кратного 2 мм в большую сторону.
5.Выполняют проверку прочности принятого сечения по формуле
N/A ≤ R,
(в)
где А — принятая площадь поперечного сечения стержня. Она не равна
требуемой площади, полученной по формуле (а), так как за редким
исключением площадь сечения, приведенная в прил. I, не совпадает с
требуемой, кроме того, принятый диаметр, как правило, округляется и
принимается большим, чем требуемый.
Прочность стержня считается обеспеченной, если условие (в)
удовлетворено, и необеспеченной, если оно не удовлетворено.
Пример. Подобрать сечение стержня (подвески), поддерживающего брус
АВ, как показано на рис. 11. Материал — сталь марки С-235.
Решение. 1. Мысленно отбрасываем стержень, заменяя его действие на
брус усилием N. Направим его вверх, полагая, что он уравновешивает
нагрузку, направленную вниз.
2. Определим величину усилия N, составив уравнение равновесия ∑ Ме = 0,
которое для заданной схемы примет вид
l+а
- а) + Fa = 0,
2
где h = lcos 15° = 7 • 0,966 = 6,76 м.
Nh - q (l + а ) (
После подстановки известных величин получим
N· 6,76 – 6 0 · 8 · 3 + 3 0 · 1 = 0 ,
6
откуда
N=
60· 8 ·3 - 30·1
6,76
=
1410
6,76
= 208,6 кН.
3. Определим требуемую площадь поперечного сечения стержня по формуле
(а):
АТР =
208,6 кН
230 МПа
=
208,6· 1 0 - 3 МПа
230 МПа
=
= 0,907· 1 0 - 3 м 2 = 9 , 0 7 с м 2 ,
где R = 230 МПа для стали марки С-235 (см. прил. VIII).
4. По найденной площади определим требуемый профиль (номер)
равнополочного уголка. На два уголка требуется 9,07 см2, на один — А1 =
4,535 см2. По табл. 1 прил. I подбираем уголок 50х50x5 площадью 4,80 см2.
На два уголка площадь А = 9,6 см2.
5.Выполним проверку прочности принятого сечения по формуле (в):
N
А
=
208,6 кН
9,6 см2
=
208,6· 1 0 - 3 МПа
9,6· 1 0 - 4 м 2
=
= 217,3 МПа < 230 МПа,
учитывая, что 1 МН/м2 = 1 МПа. Прочность стержня обеспечена, так как
условие (в) удовлетворено.
Ответ: Для стержня принято сечение из двух уголков 50х50x5.
Аналогично ведется расчет на подбор сечения колонны из швеллеров,
которые приведены в задании для РГР №1.
7
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1
Тема: Осевое растяжение и сжатие.
Цель работы: Научиться выполнять расчеты на прочность..
ЗАДАНИЕ.
Подобрать
сечение
стержня-подвески
(колонны),
поддерживающего брус АВ. Материал стержня для фасонных профилейпрокатная сталь С-245, для круглого сечения- сталь арматурная
горячекатаная класса А-1.
Данные для различных вариантов приведены на рисунках
8
9
10
11
РАЗДЕЛ 3
СТАТИКА СООРУЖЕНИЙ
Расчетно-графическая работа №2
Тема: Изгиб прямого бруса.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Для решения данных задач необходимо изучить тему: Изгиб прямого
бруса, научиться быстро и безошибочно строить эпюры поперечных сил Qx и
изгибающих моментов М х .
Поперечная сила в рассматриваемом сечении численно равна
алгебраической сумме проекций на ось, перпендикулярную оси балки всех
сил, действующих по одну сторону от этого сечения.
Если при определении поперечной силы рассматривается левая
отсеченная часть балки, то внешние силы, направленные вверх, надо
принимать со знаком плюс, а вниз — со знаком минус, при рассмотрении же
правой отсеченной части — наоборот. Для построения эпюры Qx проводят
нулевую линию под изображением балки. Тогда каждому сечению балки
соответствует определенная точка этой линии. Положительные значения
поперечных сил откладывают в принятом масштабе перпендикулярно
нулевой линии вверх от нее, отрицательные — вниз. В сечениях с
сосредоточенно приложенной силой на эпюре Qx возникает скачок (два
значения — слева и справа от сечения), по абсолютному значению равный
сосредоточенной силе.
Изгибающий момент в сечении балки численно равен алгебраической
сумме моментов всех внешних сил, действующих по одну сторону от
рассматриваемого сечения, относительно центра тяжести данного сечения.
Моменты,
вызывающие
растяжение
нижних
волокон,
считают
положительными, а верхних — отрицательными. Из этого правила знаков
вытекает, что если моменты внешних сил стремятся повернуть левую
отсеченную часть балки относительно центра рассматриваемого сечения по
часовой стрелке, то эти моменты надо брать со знаком плюс» а против
часовой стрелки — со знаком минус; при рассмотрений же правой части —
наоборот. При построении эпюры М у строителей принято: ординаты,
выражающие в определенном масштабе значения изгибающих моментов,
откладывать со стороны растянутых волокон, т. е. положительные — вниз, а
отрицательные — вверх от оси балки. Два значения изгибающего момента
появляются в сечениях, где приложен сосредоточенный момент (пара сил).
На эпюре соответственно возникает скачок, равный сосредоточенному
моменту.
Построенные эпюры Q и М заштриховывают прямыми линиями,
перпендикулярными нулевой линии. Каждый штрих таким образом
характеризует значение внутреннего силового фактора Qх или М х,
действующих в данном сечении балки. Знак на эпюре ставится всегда, а на
12
эпюре М х знака можно не ставить, так как она всегда строится со стороны
растянутых волокон.
Пример 1. Построить эпюры поперечных сил и изгибающих моментов
длябалки, нагруженной согласно схеме рис. 18,а и подобрать сечение из
стального двутавра по методу допускаемых напряжений при [ σ] стали =
160МПа и по методу расчетных предельных состояний при R = 210 МПа
Р е ш е н и е . Определяем опорные реакции балки.
Проверка правильности определения опорных реакций:
Следовательно, реакции определены правильно.
Построение эпюры Q
В сечении АC поперечная сила численно равна соответствующей
опорной реакции и положительна, т. е.
На участке балки АС до сечения С нагрузка отсутствует, следовательно,
поперечная сила до этого сечения постоянна по величине и знаку. В сечении
С приложена сосредоточенная сила Р = 3 2 кH и направлена в сторону,
противоположную направлению опорной реакции. В этом сечении величина
QС
выразится разностью
До точки D поперечная сила QС своей величины не изменяет. На участке
же DE поперечная сила изменяется по линейному закону. Для построения
эпюры на этом участке необходимо знать два значения поперечной силы:
QD и QЕ. Первое из них QD = 4,2 кH, а QЕ = QD – qa3 = 4,2—12 • 3= — 31,8
кH
Откладываем на оси в точке Е (вниз) ординату, выражающую QЕ (рис.
13
18,б).
Далее поперечная сила будет иметь постоянное значение до точки В, так
как проекция пары сил на любую ось равна нулю и не влияет на очертание
эпюры поперечных сил. Таким образом, QB = VB = —31,8 кH.
Как видим, поперечные силы в опорных точках A и В численно равны
опорным реакциям, что означает правильное построение эпюры Q.
Построение эпюры М
В сечении А изгибающий момент равен нулю: МА = 0.
В сечении С изгибающий момент
Изгибающий момент в сечении D
Далее следует определить на участке DЕ положение сечения (абсциссу
Z0) в котором поперечная сила равна нулю, и, следовательно, наибольший
изгибающий момент.
Абсцисса Z0 может быть определена из подобия треугольников эпюры Q
на участке DЕ балки
По полученным. значениям изгибающих моментов в сечениях балки
строим эпюру М (рис. 18, в).
Абсцисса Z0 может быть определена и другим способом. Для этого
необходимо составить уравнение, выражающее равенство нулю суммы проекций всех сил на ось у слева или справа от точки 0:
14
Подбор сечения стальной двутавровой балки
по методу допускаемых напряжений
По наибольшему изгибающему моменту
По наибольшему изгибающему моменту определяем требуемый момент
сопротивления сечения
Из таблицы сортамента (см. приложение в конце пособия) находим сечение двутавра, близкое к требуемому: № 36 с моментом сопротивления WХ
=743 см3
Подбор сечения балки по методу расчетных предельных состояний
Определяем расчетные нагрузки на балку, считая РН = 32 кН, q н =12
кН/м, тн= 24 кНм. По условию задачи постоянная нагрузка составляет 60%
от нормативной, а временная — 40%. Тогда нормативные нагрузки на балку
будут равны:
15
Положение точки 0 (перехода эпюры Q через нуль):
откуда
Наибольший изгибающий момент в сечении балки:
Необходимый момент сопротивления сечения
Принимаем № 33 двутавра с моментом сопротивления WХ = 597 см3. Как
видно, при заданных условиях сечение балки, рассчитанное по методу
предельных состояний, оказалось более экономичным, чем определенное по
методу допускаемых напряжений
16
Призер 2. Пользуясь результатами построения эпюр поперечных сил и
изгибающих моментов для балки, рассмотренной в примере 1 (рис. 18),
определить в ее сечениях касательные и приведенные напряжения.
Р е ш е н и е. В примере 1, в результате расчета по допускаемым напряжениям, принят для балки стальной двутавр № 36.
Из сортамента двутавровых профилей выпишем необходимые параметры
для решения задачи:
толщина стенки d = 0,75 см (0,0075 м).
Определение касательных напряжений в сечениях балки
17
Как видно из эпюры Q, наибольшая поперечная сила возникает на
участке АС балки (рис. 18, б) и равна 36,2 кН (0,0362 Мн).
Величина наибольшего касательного напряжения по нейтральной оси
балки, (сечение которой показано на рис. 19, а)
Для определения приведенного напряжения надо сначала сопоставив
эпюры Q и M, найти сечение, в котором Q и M одновременно имеют
относительно большие значения. Таким, очевидно, будет сечение С, в
котором QС = 36,2кН(0,0362МН), МС = 108,6кНм (0,109МНм)
Определяем для сечения С величину нормального напряжения
М
0,109
σс = WХ = 0,000743 = 0,000146 МПа
Нормальное напряжение на уровне сопряжения стенки с полкой (рис.
19,б) при у= 18- 1,23 ≈ 16,8 см(0,168 м)
М
0,109
σ1-1 = J у = 0,000134 0,168 = 136,6МПа
х
Статический момент площади сечения полки относительно нейтральной
оси балки
Sx-x = 14,5 · 1,23 · 17,38 = 310 см3 (0,000310 м3)
Касательное напряжение в сечении на уровне сопряжения ее с полкой
Q ·S
0,0362· 0,000310
τ1-1 = Jх·b2-22-2 = 0,000134·0,0075 = 11,2 МПа
Строим эпюру τ (рис.19,в)
Проверяем прочность балки по приведенному напряжению:
σпр =√σ +3·τ2 = √136,62 + 3·11,22 =138МПа
2
≤ 160 МПа
18
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2
Тема: Поперечный изгиб прямого бруса.
Цель работы: Научиться строить эпюры нормальных напряжений,
изгибающих моментов и др..
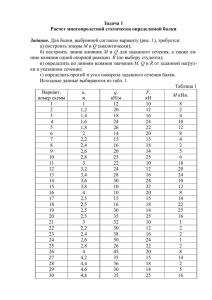
ЗАДАНИЕ. Для балки с нормативной нагрузкой построить эпюры Q и М и
подобрать сечения из двутавра. Построить эпюры касательных и
нормальных напряжений, в которых Q мах и М мах
Данные для различных вариантов указаны в таблице.
19
Данные для различных вариантов указаны в таблице
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Схема
I
II
III
IV
V
VI
VII
VIII
IX
X
Р.
кН
q,
кН/м
m,
кн/м
34
26
18
26
32
20
32
28
20
28
22
30
20
22
30
22
30
24
30
24
18
24
18
25
18
25
34
25
26
32
8
10
11
10
16
14
16
12
14
12
20
16
14
20
16
20
16
18
16
18
11
18
12
16
12
14
8
14
10
16
10
8
20
8
14
6
14
12
10
14
12
22
16
12
22
12
22
10
22
10
20
10
20
18
20
18
10
18
8
14
а1,
м
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
а2,
м
2
3
4
3
2
1
2
3
4
3
2
1
3
2
1
3
1
2
3
1
2
2
3
4
2
1
1
1
2
3
а3,
м
3
2
1
3
1
1
3
2
1
2
3
4
2
3
4
1
2
3
1
3
3
2
3
1
2
2
1
3
2
1
а4,
м
2
2
1
2
3
4
2
1
1
3
2
1
2
1
1
3
2
1
3
2
1
2
1
1
2
3
4
3
2
1
а5,
м
2
1
1
1
2
1
2
2
1
1
1
1
2
2
1
2
3
1
2
2
1
3
1
1
3
2
1
2
2
3
20
РАЗДЕЛ 3
СТАТИКА СООРУЖЕНИЙ
Расчетно-графическая работа №3
Тема: Статически определимые плоские рамы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Рамные системы широко применяют в железобетонных, металлических и
деревянных конструкциях. Одно- и многоэтажные рамы используют при
возведении фабрично-заводских корпусов, общественных зданий, складов,
башен элеваторов, мостов, трибун стадиона, для установки механизмов, при
устройстве набережных и т. д.
Определение поперечной силы, изгибающего момента продольной силы,
действующих в сечениях рамы, и построение их эпюр является начальной
стадией расчета рамных конструкций.
К решению данной задачи можно приступить после изучения темы:
Статически определимые плоские рамы (раздел «Статика сооружений).
Необходимо иметь в виду, изучение темы невозможно без твердых навыков
и прочных знаний по теме: Изгиб простого бруса (раздел «Сопротивление
материалов»).
Условие задачи. Для консольной статически определимой рамы
построить эпюры Мх, Qx, N. Проверить равновесие узла (рис. 32, а).
Для рам консольного типа эпюры Мх, Qx, N могут быть построены без
определения опорных реакций заделки, если начинать эти построения со
стороны свободного конца.
Условимся при расчете рамы мысленно ставить себя на плоскость
чертежа внутрь рамы. Тогда, повернувшись лицом к сечению, в котором
определяется внутренний силовой фактор или относительно которого
составляется уравнение равновесия, легко представить себе, какую часть
рамы следует считать левой, а какую правой. В этом случае при определении
внутренних силовых фактов для рам становится возможным пользоваться
правилами, применяемыми при построении эпюр для балок.
Решение. Построение эпюры Qx (рис. 32,б). За ось абсцисс принимаем ось
любого стержня. Перпендикулярно ей мысленно проводим ось ординат и
проецируем на нее силы, действующие соответственно слева или справа от
рассматриваемого сечения, учитывая правила знаков.
Ригель ВС. Ход справа. Поперечную силу определяем по характерным
точкам (аналогично простым балкам).
21
Стойка АС, Повернемся лицом к стойке, проведём мысленно ось
перпендикулярно оси стойки и спроецируем на нее силы ходом справа; Qс
= 0; Qx=0. Изобразим полученные результаты графически. Проведем
ломаную линию АСВ (рис. 32, б) и от нее, как от нулевой, отложим
вычисленные ординаты эпюры поперечных сил. Положительные ординаты
эпюры для ригеля откладываем вверх от нулевой линии и влево от
нулевой линии для стойки. Отрицательные соответственно вниз и вправо
от нулевой линии.
Построение эпюры Мх (рис. 32, в). Изгибающий момент в сечениях рамы
определяем также по характерным точкам ходом справа (со свободного
конца).
Стойка АС. Как и при определений поперечной силы, при переходе от
ригеля к стойке повернемся на 90° лицом к стойке. Точка С принадлежит
одновременно и ригелю и стойке, поэтому МС стойки = МС ригель = - 22 кН-м.
Так как в данной задаче непосредственно к стойке не приложены внешние
нагрузки, а плечи сил F и Q остаются неизменяемыми, то в любом сечении
от С до А изгибающий момент один и тот же МА = МС = - 22 кН-м. При
построении эпюры изгибающих моментов (как и в балках) положительные
ординаты откладываем со стороны растянутых волокон.
Построение эпюры N (рис. 32,г). Определяя продольную силу,
проецируем заданные силы на ось абсцисс, совмещая ее сначала с ригелем,
затем со стойкой. Продольная сила в любом сечении ригеля равна нулю, NСВ
= 0, так как справа от сечения действует нагрузка, перпендикулярная его
оси. Продольная сила во всех сечениях стойки постоянна, так как сама
стойка не нагружена и на ось стойки дают проекцию силы F и 2q. NСА= – F –
2q = – 5 – 4= – 9 кН. Ординаты эпюры продольных сил откладываем
симметрично по обе стороны оси рассматриваемого элемента. Знак плюс,
поставленный на эпюре N. соответствует деформации растяжения, знак
минус — сжатия.
22
Для проверки правильности построения эпюр рассмотрим равновесие
узла С. Для этого мысленно вырежем этот узел, проведя два сечения на
бесконечно близком расстоянии в ригеле справа от узла, в стойке — слева от
него.
Вырезанный таким образом узел дает возможность, рассматривая сечение
в ригеле, считать узел отнесенным к левой части ригеля, а при рассмотрении
сечения в стойке — к правой части стойки. Прикладываем к узлу С
внутренние силовые факторы Qx, Мх, N, беря их значение с эпюр с учетом
знака, показывающего направление их действия (рис. 32,д).
Из эпюры Qx, видим, что поперечная сила в сечении С ригеля
положительна. Поскольку точка С относится к левой части рамы (согласно
ранее принятому), QРИГ. согласно правилу знаков направляем вниз. На
стойке поперечная сила отсутствует.
Из эпюры Мх видим, что изгибающий момент вызывает растяжение
верхних волокон. Следовательно, с учетом правила знаков в ригеле
изгибающий момент Мс направляем по часовой стрелке, а в стойке (узел С
относим к правой части рамы) — против часовой стрелки. Продольная сила
NСА вызывает в сечении сжатие и, следовательно, должна быть направлена в
сторону этого сечения.
Для равновесия узла должны соблюдаться следующие условия:
Составим эти уравнения, направив ось х вправо, а ось у вертикально вверх:
Условия равновесия соблюдаются. Следовательно, внутренние силовые
факторы определены правильно
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3
23
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3
Тема: Статически определимые плоские фермы.
Цель работы: Научиться строить эпюры нормальных напряжений,
изгибающих моментов и др...
ЗАДАНИЕ. Построить эпюры Nx, Qx, Mx для статически определимой
рамы.
24
Данные для различных вариантов указаны в таблице.
Вариант
Схема
F1,, кН
F 2 , кН
q, кН/ м
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
50
40
50
40
10
25
60
60
40
30
40
30
20
10
50
50
30
20
30
20
10
20
40
40
80
60
50
90
70
60
50
50
30
-
15
20
10
10
15
20
10
15
15
15
10
10
15
15
10
10
15
20
15
10
10
15
20
10
15
25
МЕТОДИЧЕСКИЕ УКАЗАНИЯ.
Г р а ф и ч е с к и й р а с ч е т выполняют на основе построения
диаграмм Максвелла — Кремоны.
Вычерчиваем геометрическую схему фермы в масштабе 1:200 (в
1 см – 2 м) (рис. а). Обозначаем узлы фермы прописными
латинскими буквами, а внешние поля (контуры) ограниченные
внешними силами, — строчными русскими буквами. Внутренние
контуры, ограниченные стержнями фермы, обозначаем арабскими
цифрами. Внешние силы в соответствии с обозначением контуров
получают наименования а—б, б — в и т. д. Усилия в стержнях
обозначают в соответствии с направлением обхода узлов; например,
при обходе узла А усилия в стержнях, сходящихся в этом узле,
обозначают . а —1, 1— д, д—а.
Построение диаграммы:
Выбираем масштаб сил: в 1 см – 10 кН.
Строим замкнутый силовой многоугольник (из внешних сил)
а—б, б — в и т. д.. (рис. б).
Диаграмму усилий в стержнях строим на базе силового многоугольника начиная с узла А, в котором сходятся два неизвестных
усилия.
Из точек а и д замкнутого силового многоугольника проводим
линии, параллельные стержням фермы а—1 и 1— д, которые
пересекутся в точке 1 первого замкнутого многоугольника.
Направление усилий а—1 и 1—д указываем стрелками на
схеме фермы, которые означают, что стержень а—1 сжат, а
стержень 1—д растянут. Измерив в принятом масштабе сил
отрезки а—1 и 1— д, получим величины усилий в соответствующих
стержнях.
Переходим к узлу F, для которого замкнутый многоугольник
сил д—1—2— д; из него видно, что точки 1 и 2 совпадают, т. е.
усилие в стержне 1 — 2 равно нулю. Усилие 2—д растягивающее.
Следующим будет узел С, для которого замкнутый многоугольник
сил 2—1—а—б—3—2. Проведя от точки б линию, параллельную
стержню б—3, а от точки 2 — параллельную стержню 3—2,
получим точку пересечения их 3 и сжимающие усилия в. стержнях
б—3 и 3—2.
Далее рассмотрению подлежит узел D, для которого
замкнутый многоугольник сил будет 3—б—в—4—3. Проведя из
точки в линию, параллельную стержню фермы в—4, а из точки 4
линию, параллельную стержню 4—3, получим на диаграмме
усилий линии, выражающие усилия в стержнях фермы в—4 и 4—
26
3, из которых первое будет сжимающим, а второе —
растягивающим; направления их указываем на схеме фермы.
Таким образом, для левой половины диаграмма построена; для
правой достраиваем ее по условию симметрии. Полная диаграмма
усилий представлена на рис. б.
Определение усилий по диаграмме. По построенной диаграмме
(рис. б) измеряем расстояние между точками, соответствующими
определенному стержню, и, умножая полученное значение на
масштаб (m=10кН/м), получим значения усиления.
Найденные усилия записываем в таблицу.
Элементы фермы
Верхний пояс
Нижний пояс
Стойки
Раскосы
Усилие, кН
Наименование
стержней
«+»
растягивающее
а—1 (г—6)
—
б—3 (в—4)
—
1—д (6— д) 20
20
2—д (5—д)
0
1—2 (5—6)
10
3—4
2—3 (4—5 ) —
«-»
сжимающее
—25
— 16,6
—
—
0
—
—8,30
27
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №4
Тема: Статически определимые плоские фермы.
Цель работы: Научиться определять усилия в стержнях ферм путем
построения диаграммы Максвелла-Кремоны.
ЗАДАНИЕ. Определить усилия в стержнях фермы от полной расчетной
нагрузки путем построения диаграммы Максвелла-Кремоны. Провести
анализ усилий в поясах.
Данные для различных вариантов указаны в таблице
28
Тема: Статически определимые плоские фермы.
Вариант
Схема
Р1,, кН
Р2 , кН
Р3, кН
a, м
b, м
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
I
II
III
IV
V
VI
VII
VIII
IΧ
Χ
I
II
III
IV
V
VI
VII
VIII
IΧ
Χ
I
II
III
IV
V
VI
VII
VIII
IΧ
Χ
10
12
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
12
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
26
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
26
28
30
10
12
14
16
18
20
22
24
26
28
3
3,2
3,4
3,6
3,8
4
3
3,2
3,4
3,6
3,8
4
3
3,2
3,4
3,6
3,8
4
3
3,2
3,4
3,6
3,8
4
3
3,2
3,4
3,6
3,8
4
3,2
3,4
3,6
3,8
4
3,2
3,4
3,6
3,8
4
3,2
3,4
3,6
3,8
4
3,2
3,4
3,6
3,8
4
3,2
3,4
3,6
3,8
3,2
3,4
3,6
3,8
4
3,2
29
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №5
Тема: Основы расчета статически неопределимых систем методом сил.
Цель работы: Научиться расчету неразрезных балок с помощью таблиц.
ЗАДАНИЕ. Построить эпюры Q и M для неразрезной балки.
30
Данные для различных вариантов указаны в таблице
Вариант
Схема
F1,, кН
F 2 , кН
q, кН/ м
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
50
40
100
50
40
10
25
20
60
60
40
30
90
40
30
20
10
10
50
50
30
20
80
30
20
10
20
20
40
40
60
50
40
80
60
40
70
60
50
90
70
50
40
30
70
50
50
30
12
20
12
16
10
8
16
20
6
12
10
15
10
15
15
10
15
15
10
10
15
20
15
15
10
10
15
20
10
15
31
Пример Для неразрезной балки построить эпюры Q и М.
Дано: F1=40 кН; q=8 кН/м; F2=20 кН.
32
33
34
35
ПРИЛОЖЕНИЕ
36