45
реклама

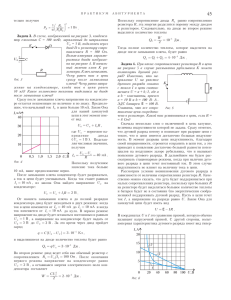
ÏÐÀÊÒÈÊÓÌ ÀÁÈÒÓÐÈÅÍÒÀ ñÿ äî íåêîòîðîãî ìàêñèìàëüíîãî íàïðÿæåíèÿ. ×åìó áóäåò ðàâíî ýòî íàïðÿæåíèå? Ïîñëå çàìûêàíèÿ êëþ÷à K ìû áóäåì èìåòü êîëåáàòåëüíûé êîíòóð, ñîñòîÿùèé èç çàðÿæåííîãî êîíäåíñàòîðà åìêîñòüþ C è êàòóøêè èíäóêòèâíîñòüþ L1 . Êîíäåíñàòîð íà÷íåò ðàçðÿæàòüñÿ, è êîãäà íàïðÿæåíèå íà íåì ñòàíåò íóëåâûì, íà÷àëüíàÿ ýíåðãèÿ êîíäåíñàòîðà ïîëíîñòüþ ïåðåéäåò â ýíåðãèþ ìàãíèòíîãî ïîëÿ êàòóøêè. Åñëè â ýòîò ìîìåíò òîê ÷åðåç êàòóøêó ðàâåí IL , òî ìîæíî çàïèñàòü CU02 L1IL2 . = 2 2 Îòñþäà íàõîäèì èñêîìûé òîê: C IL = U0 L1 . Îòñþäà ïîëó÷àåì Ýòî ìàêñèìàëüíûé òîê ÷åðåç êàòóøêó èíäóêòèâíîñòüþ L1 , çàòåì îí íà÷íåò óìåíüøàòüñÿ, ïðè ýòîì ÷àñòü åãî áóäåò ïåðåçàðÿæàòü êîíäåíñàòîð, à ÷àñòü ïîòå÷åò ÷åðåç êàòóøêó èíäóêòèâíîñòüþ L2 . Ïóñòü â íåêîòîðûé ìîìåíò ÷åðåç ïåðâóþ êàòóøêó òå÷åò òîê I1 , à ÷åðåç âòîðóþ òîê I2 . Òîãäà ïî çàêîíó Îìà äëÿ êîíòóðà, îõâàòûâàþùåãî îáå êàòóøêè, ìîæíî çàïèñàòü dI dI L1 1 + L2 2 = 0 . dt dt Ðåøåíèå ýòîãî óðàâíåíèÿ èìååò âèä L1I1 + L2 I2 = const . Êîíñòàíòó íàéäåì èç íà÷àëüíûõ óñëîâèé.  òîò ìîìåíò, êîãäà òîê ÷åðåç êàòóøêó èíäóêòèâíîñòüþ L1 áûë ìàêñèìàëåí è ðàâåí U0 C L1 , òîê ÷åðåç êàòóøêó èíäóêòèâíîñòüþ L2 áûë ðàâåí íóëþ, ñëåäîâàòåëüíî, 45 Um = U0 L2 . L1 + L2 Çàäà÷à 3. Ïðè ðàçîìêíóòîì êëþ÷å K (ðèñ.3) êîíäåíñàòîð åìêîñòüþ C = 20 ìêÔ çàðÿæåí äî íàïðÿæåíèÿ U0 = 12 B , ÝÄÑ àêêóìóëÿòîðà E = 5 Â, C L èíäóêòèâíîñòü êàòóøêè L = = 2 Ãí, D èäåàëüíûé äèîä. + U0 E Êàêèì áóäåò ìàêñèìàëüíûé òîê â öåïè ïîñëå çàìûêàíèÿ êëþ÷à? ×åìó áóäåò ðàâíî íàïðÿæåíèå íà êîíäåíñàòîðå â D óñòàíîâèâøåìñÿ ðåæèìå ïîñëå çàìûêàíèÿ êëþ÷à? K Ïîñêîëüêó â ñõåìå íàõîäèò- Ðèñ. 3 ñÿ êàòóøêà èíäóêòèâíîñòè, ñðàçó ïîñëå çàìûêàíèÿ êëþ÷à òîê â öåïè áóäåò ðàâåí íóëþ, çàòåì áóäåò ïðîèñõîäèòü íàðàñòàíèå òîêà, è â íåêîòîðûé ìîìåíò îí äîñòèãíåò ìàêñèìàëüíîãî çíà÷åíèÿ. Ïðè ìàêñèìàëüíîì òîêå â öåïè ÝÄÑ èíäóêöèè â êàòóøêå áóäåò ðàâíà íóëþ, è ïî çàêîíó Îìà äëÿ çàìêíóòîé öåïè íàïðÿæåíèå íà êîíäåíñàòîðå â ýòîì ñëó÷àå äîëæíî áûòü ðàâíî ÝÄÑ àêêóìóëÿòîðà. Îáîçíà÷èì ýòî íàïðÿæåíèå ÷åðåç U1 (U1 = E ) è íàéäåì âåëè÷èíó ìàêñèìàëüíîãî òîêà. Äëÿ ýòîãî âîñïîëüçóåìñÿ çàêîíîì ñîõðàíåíèÿ ýíåðãèè. Çà âðåìÿ óñòàíîâëåíèÿ ìàêñèìàëüíîãî òîêà â öåïè ïðîòåê çàðÿä ∆q = CU0 − ÑU1 = C (U0 − U1 ) . Äëÿ ïåðåìåùåíèÿ ýòîãî çàðÿäà ïðîòèâ ÝÄÑ àêêóìóëÿòîðà íåîáõîäèìî ñîâåðøèòü ðàáîòó A = ∆qE = ÑE (U0 − U1 ) . L1I1 + L2 I2 = U0 L1C . Íàëè÷èå ìàêñèìàëüíîãî òîêà Im â êàòóøêå ïðèâîäèò ê ïîÿâëåíèþ ýíåðãèè ìàãíèòíîãî ïîëÿ 1 WL = LIm2 . 2 Êîãäà íàïðÿæåíèå íà êîíäåíñàòîðå äîñòèãíåò ìàêñèìàëüíîãî çíà÷åíèÿ, òîê ÷åðåç êîíäåíñàòîð áóäåò ðàâåí íóëþ, à ÷åðåç êàòóøêè áóäåò òå÷ü îáùèé òîê, êîòîðûé îáîçíà÷èì ÷åðåç I12 . Èñïîëüçóÿ ïðåäûäóùåå ñîîòíîøåíèå, ìîæíî çàïèñàòü Ðàçíîñòü ýíåðãèé êîíäåíñàòîðà â íà÷àëüíîì è êîíå÷íîì ñîñòîÿíèÿõ ðàâíà ñóììå ñîâåðøåííîé ðàáîòû è ýíåðãèè êàòóøêè: 1 1 1 CU02 − CU12 = A + WL = CE (U0 − U1 ) + LIm2 . 2 2 2 const = U0 LC 1 . Òîãäà ðåøåíèå ïðèíèìàåò âèä (L1 + L2 ) I12 = U0 L1C , îòêóäà I12 = U0 L1C . L1 + L2 Ïóñòü ìàêñèìàëüíîå íàïðÿæåíèå íà êîíäåíñàòîðå ðàâíî Um . Ïîñêîëüêó â íàøåé öåïè íåò òåïëîâûõ ïîòåðü, äëÿ ëþáîãî ìîìåíòà âðåìåíè ìû ìîæåì âîñïîëüçîâàòüñÿ çàêîíîì ñîõðàíåíèÿ ýíåðãèè. Ïîëíàÿ ýíåðãèÿ öåïè, î÷åâèäíî, ðàâíà CU02 2 .  òîò ìîìåíò, êîãäà êîíäåíñàòîð ïåðåçàðÿäèòñÿ è íàïðÿæåíèå íà íåì äîñòèãíåò ìàêñèìàëüíîãî çíà÷åíèÿ, ÷àñòü ýíåðãèè áóäåò ñîñðåäîòî÷åíà â êîíäåíñàòîðå: 1 WC = CUm2 , 2 à îñòàëüíàÿ ÷àñòü â êàòóøêàõ èíäóêòèâíîñòè: WL = 1 1 L1CU02 2 L1 + L2 ) I12 = ( . 2 2 L1 + L2 Ïî çàêîíó ñîõðàíåíèÿ ýíåðãèè, 2 1 1 1 LCU 1 0 . CU02 = CUm2 + 2 2 2 L1 + L2 Îòñþäà íàõîäèì Im = (U0 − E ) C ≈ 0,022 A . L Òåïåðü ðàññìîòðèì âîïðîñ îá óñòàíîâèâøåìñÿ çíà÷åíèè íàïðÿæåíèÿ íà êîíäåíñàòîðå. Ïîñëå ïðîõîæäåíèÿ ìàêñèìóìà òîê â öåïè áóäåò óìåíüøàòüñÿ è â êîíå÷íîì èòîãå ñòàíåò ðàâíûì íóëþ. Ïîñêîëüêó òå÷ü â îáðàòíîì íàïðàâëåíèè òîê íå ìîæåò (ìåøàåò äèîä), òî óñòàíîâèòñÿ ñòàöèîíàðíîå ñîñòîÿíèå: òîê ðàâåí íóëþ, à íà êîíäåíñàòîðå èìååòñÿ íåêîòîðîå ïîñòîÿííîå íàïðÿæåíèå, êîòîðîå îáîçíà÷èì ÷åðåç Uê . Ýòî íàïðÿæåíèå ìîæíî íàéòè ïî çàêîíó ñîõðàíåíèÿ ýíåðãèè. Çà âñå âðåìÿ ñ ìîìåíòà çàìûêàíèÿ êëþ÷à äî óñòàíîâëåíèÿ ñòàöèîíàðíîãî ñîñòîÿíèÿ èçìåíåíèå ýíåðãèè êîíäåíñàòîðà ïîøëî íà ðàáîòó ïî ïåðåìåùåíèþ âñåãî ïðîòåêøåãî çàðÿäà ïðîòèâ ÝÄÑ àêêóìóëÿòîðà: 1 1 CU02 − CUê2 = CE (U0 − Uê ) . 2 2 Ïîñëå ïðîñòûõ ïðåîáðàçîâàíèé ýòî óðàâíåíèå áóäåò èìåòü âèä (U0 − Uê ) (U0 − 2E + Uê ) = 0 . Òàêîå óðàâíåíèå èìååò äâà ðåøåíèÿ. Ïåðâîå ðåøåíèå Uê = U0