Начертательная геометрия. Методическая разработка
реклама

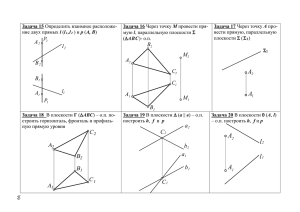
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ О.Н. Пачкория, И.В. Подзей, И.Г. Хармац НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Методическая разработка для практических занятий студентов I курса всех специальностей дневного обучения Москва – 2004 Рецензент д-р техн. наук, проф. Л.В. Михненков О.Н. Пачкория, И.В. Подзей, И.Г. Хармац. Начертательная геометрия: Методическая разработка для практических занятий студентов I курса всех специальностей дневного обучения. — М.: МГТУ ГА, 2004. – 33 с. Данное пособие издается в соответствии с учебным планом для студентов I курса специальностей 130300, 131000, 201300, 220100, 330500, 075600 дневного обучения. Рассмотрено и одобрено на заседаниях кафедры 29.04.04 и Методического совета ___________. 1. Условные обозначения При решении задач студент должен использовать терминологию, определения, обозначения, символы и понятия, рекомендуемые на лекциях и в учебной литературе [2, 3]. 1. Точки пространства обозначают прописными буквами латинского алфавита: А, В, С, D… или цифрами 1, 2, 3, 4,… 2. Прямые и кривые линии пространства — строчными буквами латинского алфавита: a, b, c, d, … 3. Плоскости и поверхности (оригиналы) — прописными буквами греческого алфавита: A(альфа), B(бета), Г(гамма), Q(тэта), L(ламбда), S(сигма), F(фи), Y(пси), W(омега), T(тау). 4. Углы обозначают строчными греческими буквами: a(альфа), b(бэта), g(гамма), j(фи), q(тэта), l(ламбда), w(о мега), t(тау), d(дельта). 5. Плоскости проекций обозначают буквой П («пи» — прописная буква греческого алфавита) с добавлением подстрочного индекса 1, 2, 3, 4, 5…, при этом: · горизонтальная плоскость проекций обозначается – П1; · фронтальная плоскость проекций – П2; · профильная плоскость проекций – П3; · новую плоскость проекций, отличную от указанных выше, обозначают: П4, П5, … 6. Проекции точек, линий и поверхностей обозначают теми же буквами, какими обозначены сами оригиналы, с добавлением индекса плоскости проекций, на которую спроецирован объект. Так, проекции точки А, прямой а и плоскости Q соответственно обозначают: · на плоскости П1 – А1, а1, Q1; · на плоскости П2 – А2, а2, Q2; · на плоскости П3 – А3, а3, Q3. 7. Рекомендуется обозначать: · линию горизонтального уровня (горизонталь) — h; · линию фронтального уровня (фронталь) — f; · линию профильного уровня (профильная прямая) — р; · плоскость горизонтального уровня — Г; · плоскость фронтального уровня — Ф; · плоскость профильного уровня — Р. 8. Последовательность точек, прямых, плоскостей и поверхностей обозначают верхним индексом 1, 2, 3, … 9. Действительную длину отрезка обозначают — dd. 10. Символы, обозначающие отношения между геометрическими объектами: 1) º — совпадение объектов. Например, (АВ) º (CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D; 2) ~ — подобие объектов. Например, DВАС ~ DMNK — треугольники АВС и MNK подобны. 3) || – параллельность объектов. Например, a||b — плоскость a параллельна плоскости b. 4) ^ — перпендикулярность объектов. Например, а^b — прямые а и b перпендикулярны. 5) ° ¾ скрещивание прямых. Например, с°d — прямые с и d скрещиваются. 3 6) Î — принадлежность объекта множеству. Например, АÎа — точка А принадлежит прямой а, т.е. точка А является значением множества точек прямой а. 7) Ì — принадлежность подмножества множеству. Например, аÌa — прямая а принадлежит плоскости a, т.е. множество точек прямой а является подмножеством точек плоскости a. 8) Ç — пересечение множеств. Например, а=aÇb - прямая а является результатом пересечения плоскостей a и b. 9) \ — логическое отрицание знака. Например, а||b \ – прямая а не параллельна прямой b. 2. Точка, прямая, плоскость 1. 2. 3. 4. 5. Свойства прямоугольного проецирования. Образование комплексного чертежа. Проецирование на три взаимно-перпендикулярные плоскости проекций. Способы задание прямой линии на чертеже. Прямые общего и частного положения. Признаки, позволяющие определять по чертежу положение прямой линии относительно плоскостей проекций. 6. Следы прямой. 7. Точка на прямой. Деление отрезка прямой в данном отношении. 8. Определение длины отрезка прямой и углов его наклона к плоскостям проекций. 9. Взаимное расположение прямых в пространстве. 10. Конкурирующие точки. Относительная видимость точек скрещивающихся прямых. 11. Проецирование прямого угла. 12. Способы задание плоскости на чертеже. 13. Плоскости общего и частного положения. Свойства прецирующих плоскостей. 14. Прямые и точки, принадлежащие плоскости. 15. Особые линии плоскости. 16. Следы плоскости. 17. Параллельность прямой и плоскости. Параллельность плоскостей. 18. Перпендикулярность прямой и плоскости. Перпендикулярность плоскостей. 19. Перпендикулярность прямых общего положения. 20. Построение точки пересечения прямой и плоскости. Определение видимости прямой линии относительно плоскости. 21. Построение линии пересечения двух плоскостей. 4 Задача 1 По заданным изображениям точек A, B, C, D, E. F, G, K построить их комплексные чертежи. Определить, в какой четверти пространства находится каждая точка. Ï2 À2 40 À Õ1 2 Ï2 Â1 2 À1 2 30 Õ1 2 Â1 2 À1 2 Ï1 À1 Ï1 35 Â1 15 Â2  C 40 Ï2 C2 Õ1 2 45 D1 25 C1 Õ 1 2 Ï2 C1 2 D1 2 Ï1 D 35 D1 2 C1 2 Ï1 D2 Ï2 Eº E1 45 F1 2 Õ1 2 G1 2 K1 2 25 Kº K2 Õ1 2 40 E1 2 Ï2 E1 2 F1 2 G1 2 K1 2 Ï1 35 Gº G1 Ï1 Fº F2 Задача 2 По заданным координатам точек А (15,10,20), В (25,20,-35), С (40,-30,45), D (50,45,0), E (65,0,70) построить их проекции на три плоскости проекций. Задача 3 1. Построить две проекции следующих точек: А(20,20,100); В(50,70,90); С(80,30,90); D(100,30,0); Е(0,50,50) 2. Заполнить таблицу: Расположение от плоскостей проекций П1 П2 П3 max min 5 3. Определить, на каком расстоянии от плоскостей проекций расположены точки, и заполнить таблицу: Точка Плоскость проекций Расстояние А П1 В П2 С П3 Задача 4 Построить фронтальную проекцию точки А при условии, что точка А: · удалена от П1 на 10 мм; · расположена в плоскости П1. X1 2 Ï2 Ï1 A1 Задача 5 Построить горизонтальную проекцию точки В при условии, что точка В расположена вдвое ближе к плоскости П1, чем к П2. B2 x1 2 Ï2 Ï1 Задача 6 На каждом из чертежей прямой CD построить точки: · А – удаленную от плоскости П1 на 30 мм; · В – удаленную от плоскости П2 на 10 мм. Ñ2 Ï2 Ï2 Ï1 Ï3 Ñ2 D2 Ï1 Ñ1 D1 D2 C1 D1 Задача 7 Назвать прямые, заданные на чертеже. Построить проекции отрезка АВ длиной 15 мм. Определить углы наклона прямых к плоскостям проекций. À2 À2 h2 z À2 À2 f2 À2 º Ñ2 x x À1 À1 º À1 6 h1 À1 À1 f1 Ñ1 y Задача 8 Построить профильную проекцию отрезка прямой АВ. Определить натуральную величину отрезка АВ. z A2 B2 x A1 B1 y Задача 9 Определить взаимное расположение прямой а и точек, заданных на чертежах. a2 B2 C2 A2 a2 E2 E2 D2 D2 x D1 A1 B1 C1 Ï2 x1 2 Ï1 E1 D1 a1 º E1 a1 Задача 10 Задача 11 Через точку В провести горизонПостроить проекции отрезка АВ, если таль и фронталь, пересекающие прямую а. известно, что отрезок прямой АВ: · проходит через заданную точку А; B2 · параллелен П2; a2 · наклонен к П1 под углом 30°; · имеет длину 40 мм. x À2 B1 Ï2 Ï1 a1 À1 7 Задача 12 Определить взаимное расположение прямых линий m и l. m2 m2 l2 l2 m1 m1 l1 m l1 l à) m2 m1 m l1 l m á) l â) Задача 13 Через точку С провести прямую q так, чтобы: q || m qÇm m2 l2 q°m m2 m2 C2 C2 C2 C1 C1 C1 m1 m1 m1 Задача 15 Задача 14 Построить проекции ромба ABCD, Определить взаимное расположение прямых а и b. Определить видимость точек 1-2 и если одна его сторона АВ принадлежит пря3-4. мой h, а сторона AD — прямой f. Длина стороны ромба 30 мм. â2 32º 42 À2 h2 12 22 à2 f2 õ 31 11º 21 8 À1 â1 41 h1 à1 Задача 16 Задача 17 Через точку А построить прямую с, пеПостроить горизонтальный и фронресекающую прямые a и b. тальный следы прямой АВ. Построить проекции точки С, делящей отрезок АВ в отношении: AC 3 = A 2 CB 5 a2 b2 Â2 x À2 A1 a1 b1 Â1 À1 Задача 18 Задача 19 Определить натуральную величину отНа прямой n построить точку В, ударезка прямой CD и углы его наклона к плоско- ленную от точки А на расстояние 30 мм. стям П1, П2. n2 D2 A2 Ñ2 Ï2 Ï1 Ñ1 n1 A1 D1 Задача 20 Задача 21 Построить фронтальную проекцию точПостроить горизонтальную проекцию ки А, принадлежащей плоскости S(аÇb) и оп- отрезка прямой АВ, если угол наклона пряределить натуральную величину отрезка пря- мой к фронтальной плоскости проекций 30°. мой ОА. B2 a2 b2 O2 A2 a1 b1 O1 A1 A1 9 Задача 22 Задача 23 Построить недостающие проекции пряПостроить отрезок АВ, принадлежамой l и точки А, принадлежащих плоскости щий плоскости (l, D) (m||n). l m2 2 A2 l1 D1 l1 A1 n1 m1 D2 B2 n2 Задача 24 Определить расположение в пространстве плоскостей, заданных на чертеже. b2 a2 G2 b1 f2 d2 W2 W1 d1 c1 B2 0 0 f1 ºh2 h1 a1 c2 C2 A2 0 0 S1 C1 F1 A1 B1 Задача 25 Задача 26 В треугольнике АВС построить недосДостроить горизонтальную проекцию тающие проекции точек E, F, M, N, если они плоского пятиугольника ABCDE. принадлежат плоскости АВС. C2 B2 B2 M2 E2 A2 B1 A1 F1 A1 N1 C1 D2 E2 C2 B1 10 A2 C1 Задача 27 На двух чертежах построить недостающие проекции прямой l и точки А, принадлежащих плоскости S. m2 A2 m2 A2 n2 n2 n1 n1 l1 l1 m1 m1 S (m|| n) S (mÇ n) Задача 28 Построить недостающую треугольника, принадлежащего S(hÇf). Задача 29 проекцию В плоскости АВС найти точку М, удаплоскости ленную от плоскости проекций П1 на 30 мм, а от плоскости П2 на 20 мм. C2 f2 B2 B2 A2 h2 A2 C2 x1 2 f1 A1 C1 B1 h1 Задача 30 Провести прямые уровня, лежащие в заданных плоскостях. a2 B2 b2 C2 a2 A2 b2 A2 a2 B1 b1 a1 a1 C1 b1 A1 a1 f2 ° A1 f2 h2 f1 °º h2 ° f1 S1 h1° h1 11 Задача 31 Задача 32 В плоскости, заданной пересекающимиВ плоскости S(АВС) построить пряся прямыми АВ и ВС провести горизонталь, мые, параллельные горизонтальной и фронудаленную от горизонтальной плоскости про- тальной плоскости проекций. екций на 20 мм, и фронталь, удаленную от B2 фронтальной плоскости на 30 мм. C2 A2 A2 C2 B2 C1 B1 C1 A1 A1 B1 Задача 33 Определить прямых АВ и CD. взаимное Задача 34 Через точку М провести плоскость расположение параллельную плоскости S(АВС). B2 A2 C2 M2 A2 D2 B2 C2 B1 A1 C1 C1 B1 A1 D1 Задача 35 Задача 36 Через точку К провести прямую паралЧерез точку К провести плоскость лельную горизонтальной плоскости проекций параллельно к прямым а ° b. и плоскости W(А, а). b2 a2 a2 K2 K2 A2 a1 K1 12 A1 a1 b1 K1 Задача 37 Задача 38 Через точку К провести плоскость, паОпределить точку пересечения пряраллельную прямым а и b. мой l с плоскостью Г. a2 b2 K2 l2 K1 l1 b1 a1 Ã2 Задача 40 Задача 39 Определить точку пересечения пряОпределить точку пересечения прямой n с плоскостью S(ABC). Определить видимость мой l с плоскостью S(ABC). Определить видимость элементов, считая плоскость непроэлементов, считая плоскость непрозрачной. зрачной. C2 n 2 l2 B2 B2 A2 A2 B1 C2 B1 A1 n1 C1 l1 A1 C1 Задача 41 Задача 42 Определить точку пересечения прямой l Построить точку пересечения прямой с плоскостью S(ABC). Определить видимость l с плоскостью S(АВС). Определить видиэлементов, считая плоскость непрозрачной. мость элементов, считая плоскость непрозрачной. l2 D2 A2 B2 l2 C2 A2 E2 C2 E1 C1 B1 A1 B2 B1 A1 l1 D1 l1 C1 13 Задача 43 Задача 44 Построить точку пересечения прямой l с Построить линию пересечения двух плоскостью S(аÇb). Определить видимость плоскостей S(ABC) и W(CDE). Определить элементов, считая плоскость непрозрачной. видимость элементов, считая плоскости непрозрачными. l2 a2 B2 D2 b2 E2 A2 a1 F2 C2 E1 l1 b1 C1 D1 A1 F1 B1 Задача 45 Задача 47 Построить линию пересечения двух Построить линии пересечения плосплоскостей S(ABC) и W(CDE). Определить ви- кости S(аÇb) с горизонтальной и фронтальдимость элементов, считая плоскости непро- ной плоскостью проекций. зрачными. b2 a 2 B2 D2 A2 C2 F2 E2 A1 x1 2 E1 B1 b1 D1 F1 C1 14 a1 Задача 46 Построить линию пересечения двух плоскостей S(аÇb) и W(c||d). b2 a2 c2 c1 b1 a1 d2 d1 Задача 48 Задача 49 Через точку А провести прямую, паОпределить кратчайшее расстояние от раллельную плоскости S(аÇb) и пересекаю- точки А до прямой f. щую прямую m. f2 a2 m2 A2 À2 b2 a1 A1 m1 f1 A1 b1 Задача 51 Задача 50 Построить проекции квадрата ABCD со Построить проекции равнобедренного прямоугольного треугольник АВС, гипотенуза стороной ВСÌn. которого принадлежит прямой f. A2 f2 A2 n2 f1 n1 A1 A1 15 Задача 52 Задача 53 Построить проекции общего перпенПостроить проекции прямоугольного треугольника АВС с гипотенузой АС, если: дикуляра к двум прямым m ° l. АС=50мм, ВС=30мм, ВСÌh, АВÌl (В=hÇl). l2 l2 m2 h2 B2 l1 h1 m1 B1 Задача 54 Задача 55 Фронтальная проекция квадрата имеет Из точки К опустите перпендикуляр на вид прямоугольника. Построить горизонталь- прямую l. ную проекцию. l2 K B2 2 C2 A2 l1 K1 D2 A1 Задача 56 Определить натуральную величину расстояния от точки А до осей координат. z2 3 z2 3 z2 3 x1 2 x1 2 x1 2 y1 3 до Ох 16 y1 3 до Оy y1 3 до Оz Задача 56(а) Задача 56(б) Построить проекции точки N, симметОпределить кратчайшее расстояние от ричной точке М относительно плоскости Г. точки М до плоскости Ф(АВС). Ì2 M2 À2 Â2 M1 Ñ2 Â1 G1 Ì1 À1 Ñ1 Задача 57 Задача 58 Через точку А плоскости S(АВС) проЧерез точку А плоскости S(аÇb) провести отрезок АК^S, |АК|=20 мм. вести отрезок АD^S, |АD|=30 мм. B2 a2 A2 A2 b2 C2 A1 a1 C1 A1 b1 B1 Задача 59 Задача 60 Построить геометрическое место тоЧерез точку А провести плоскость, чек, равноудаленных от концов отрезка АВ. перпендикулярную к прямой m. B2 m2 A2 A2 A1 B1 m1 A1 17 Задача 62 Задача 61 Построить точку М, симметричную Определить кратчайшее расстояние от точке N относительно плоскости S(m||n). точки D до плоскости S(АВС). N2 m2 D 2 n2 A2 C2 B2 x1 2 A1 C1 B1 n1 D1 N1 m1 Задача 63 Задача 64 Найти проекции точки D из условий: Через прямую а провести плоскость, D=lÇc, l^b, АÎl. перпендикулярную плоскости S(m||n). b2 m2 n2 a2 c2 b1 n1 m1 c1 a1 A1 Задача 65 Задача 66 Построить равнобедренный треугольВ плоскости S(АВС) построить множеник АВС с основанием АВ и вершиной СÎl. ство течек, равноотстоящих от двух заданных точек E и F. A2 E2 l2 B2 B2 A1 l1 18 A2 A1 B1 C2 F2 B1 F1 C1 E1 Задача 67 Задача 68 Построить геометрическое место тоЧерез точку А провести прямую l, пачек, удаленных от плоскости S(АВС) на рас- раллельную плоскости S(m||n) и пересекаюстояние 30 мм. щую прямую с. m2 B2 n2 C2 A2 c2 A2 B1 A1 n1 A1 c1 C1 m1 Задача 69 Задача 70 Через точку М провести плоскость, Через точку М провести плоскость D исперпендикулярную плоскости S(АВС). ходя из условий: D^S(АВС), D^W(aÇb). B2 B2 a2 b2 M2 A 2 C2 B1 C2 A2 B1 M1 M1 a1 M2 A1 A1 C1 C1 b1 Задача 71 1. 2. 3. 4. 5. 6. 7. X Y Z А 100 15 20 В 120 45 75 С 65 55 40 М 80 10 75 По заданным координатам построить проекции треугольника АВС и точки М. В плоскости треугольника АВС найти точку К, ближайшую к точке М. Построить проекции точки N, симметричной точке М относительно плоскости треугольника ABC. Определить кратчайшее расстояние от точки М до плоскости треугольника ABC. Через точку М провести плоскость, перпендикулярную плоскости треугольника АВС. Через точку N построить плоскость параллельную плоскости треугольника АВС. Определить видимость прямой MN и плоскости треугольника АВС, считая плоскость непрозрачной. 19 3. Преобразование чертежа 1. 2. 3. 4. 5. Цель преобразования чертежа. Сущность способа замены плоскостей проекций. Замена одной плоскости проекций. Замена двух плосостей проекций Сущность способа вращения вокруг проецирующей прямой. Задача 72 Определить натуральную величину отрезка прямой АВ и углы его наклона к горизонтальной и фронтальной плоскостям проекций, если А(60,30,25), В(20,15,0). Задача 73 X 60 20 40 А В С Y 30 15 10 Z 25 0 35 1. Через точку С провести прямую l параллельно отрезку АВ. 2. Определить расстояние от точки С до прямой АВ. 3. Определить расстояние между прямой l и отрезком АВ. Задача 73 Построить недостающую проекцию прямой m, если m||n и расстояние между ними равно 30 мм. m2 n2 Задача 74 Определить величину двугранного угла CABD. A2 B2 C2 x1 2 x1 2 A1 n1 B1 C1 20 D2 D1 Задача 75 Задача 76 Из точки К опустите перпендикуляр на На прямой АВ построить точки на распрямую l. стоянии 30 мм от прямой h. B2 l2 K2 A2 l1 K1 h2 x1 2 B1 h1 A1 Задача 77 Определить кратчайшее между прямыми а и b. b2 расстояние a2 Задача 78 Даны проекции одной стороны квадрата (AB) и направление другой. Построить проекции квадрата. B2 A2 x1 2 x1 2 a1 B1 b1 A1 Задача 79 Задача 80 На прямой n построить точку В, удаОпределить центр окружности, впиленную от точки А на расстояние 30 мм. санной в треугольник АВС. B2 n2 A2 A2 C2 x1 2 C1 A1 B1 n1 A1 21 Задача 81 Задача 82 Построить точку пересечения прямой l Построить линию пересечения двух и плоскости S(АВС). Определить видимость плоскостей S(ABC) и W(CDE). Определить элементов, считая плоскость непрозрачной. видимость элементов, считая плоскости непрозрачными. B2 A2 D2 l2 C2 A2 C2 F2 E2 B2 B1 E1 A1 B1 A1 D1 F1 C1 l1 C1 Задача 83 Задача 84 Определить кратчайшее расстояние от Определить кратчайшее расстояние от точки D до плоскости S(АВС). точки D до плоскости S(m||n). D2 D2 A2 C2 B2 x1 2 n2 m2 A1 C1 D1 m1 D1 B1 n1 Задача 85 Задача 86 Построить геометрическое место тоЧерез точку А плоскости S(АВС) провести отрезок АK, если АK^S и ddAK=20 мм. чек, равноудаленных от точек А, В и С. B2 B2 A2 A2 x1 2 A1 C1 B1 22 B1 C2 C2 A1 C1 Задача 87 Построить точку М, симметричную точке N относительно плоскости S(m||n). N2 m2 Задача 88 1. Найти центр окружности О, описанной около треугольника АВС. 2. Из центра О восставить перпендикуляр к плоскости треугольника ОМ=40 мм. n2 X 100 60 10 А В С Y 80 10 60 Z 10 80 50 n1 m1 N1 Задача 89 Задача 90 Определить натуральную величину Определить натуральную величину ототрезка АВ вращением вокруг проецирующей резка прямой АВ вращением вокруг проеципрямой. рующей прямой. B2 I2 B2 A2 A2 A1 I1 A1 B1 B1 Задача 92 Задача 91 Поворотом вокруг оси i совместить На прямой n построить отрезок АВ=30мм. Задачу решить методом вращения точку А с плоскостью треугольника ВСD. B2 вокруг проецирующей прямой. n2 i2 A2 C2 D2 A2 A1 D1 A1 C1 n1 i1 B1 23 4. Кривые поверхности 1. Образование и задание кривых поверхностей. 2. Каркас, определитель и очерк поверхности. 3. Решение основных позиционных задач: 3.1.Построение недостающей проекции линии, приндлежащей поверхности, если одна ее проекция задана; 3.2.Пересечение поверхности плоскостью проецирующей и общего положения; 3.3.Построение линий пересечения поверхностей; 3.4.Построение точек пересечения линии с поверхностью; 3.5.Построение линии пересечения двух поверхностей с использованием вспомогательных плоскостей уровня. 4. Опорные (характерные) точки линии пересечения поверхностей. 5. Построение линии пересечения сечения поверхностей, одна из которых является проецирующей. Задача 93 Построить недостающие проекции точек с условием, что они принадлежат заданной поверхности. S2 S2 s P2 P2 P2 m2 m2 m1 S1 s m2 m1 m1 s S1 l2 P2 A2 i2 m2 B2 m1 s l1 C1 i1 D1 24 Задача 94 Построить недостающие проекции точек A, B, C, D, E, F с условием, что они принадлежат заданной поверхности, и указать их видимость. S2 S2 C2 A2 B2 B2 K2 C2 M2 L2 M1 K1 D1 S1 E1 A2 F1 S1 E1 D1 L1 A2 C2 C2 A2 O2 B2 E1 F1 B2 F1 O1 D1 D1 E1 Задача 95 Построить недостающие проекции точек с условием, что они принадлежат заданной поверхности, и указать их видимость. A2 B2 D2 P1 N1 E2 C2 K1 Q1 G1 L1 A2 R B2 F2 C1 D1 E1 F1 M1 25 Задача 96 Построить проекции линии пересечения поверхности заданной плоскостью. Определить натуральную величину полученного сечения. S2 S2 S2 S2 S2 S2 Î2 S1 S1 F1 C2 A2 Î1 A1 B1 S1 F || P 2 à á B2 C1 ã â Задача 97 Найти точки пересечения (K, M) прямой l с заданными поверхностями. Определить видимость точек при условии, что поверхности не прозрачны. l2 l2 O2 O1 O2 O1 l1 l1 l || Ï1 à 26 l || Ï2 á l2 R60 l2 l1 Ç60 l1 ã â l2 l2 l1 l1 ä å S2 l2 C2 A2 S2 B2 B1 A1 l1 S1 A2 C2 B2 A1 S1 C1 ж l2 B1 l1 C1 з 27 l2 l2 l1 l1 и к Задача 98 Построить проекции сквозного отверстия в пространственных фигурах, заданных на чертежах. 15 30 60 10 0 100 5 5 20 Ç90 45 10 Ç90 70 а 28 б 55 20 15 5 5 20 40 60 50 100 35 5 Ç90 Ç90 в г 100 90 50 20 Ç60 10 д 29 65 60 32 40 R60 Ç60 Ç9 0 10 60 35 е ж 100 50 Ç 60 Ç50 з 30 Задача 99 Построить линии пересечения заданных поверхностей. 20 Ç60 35 80 70 40 Ç60 Ç56 60 10 30 Ç50 15 а б Ç 70 R60 70 25 90 Ç42 100 15 Ç84 20 в г 31 90 100 70 R60 Ç60 75 10 20 Ç9 0 80 е д R35 40 40 80 80 R35 25 25 12 Ç80 Ç80 ж 32 з Задача 100 Задача 101 Определить кратчайшее расстояние от Повернуть точку А вокруг прямой I до точки А до поверхности конуса. поверхности сферы. i2 S2 A2 A2 O2 A1 A1 S1 O1 i1 а б Задача 102 Построить горизонтальные проекции и линии пересечения заданных цилиндров. Высота всех цилиндров 90 мм. Ç50 Ç 35 Ç30 Ç 35 60Å 60Å а б 33 Приложение Чертежи должны быть выполнены на формате А3 (297х420) в карандаше при помощи чертежных инструментов в соответствии с требованиями ГОСТов ЕСКД и отличаться четким и точным выполнением всех построений. Формат снабжается согласно ГОСТ 2.301-68 общей рамкой на расстоянии 5 мм от всех линий обреза формата, кроме, левой линии обреза (20 мм). В правом нижнем углу формата вплотную к рамке размещают основную надпись по ГОСТ 2.104-68, форма 1. Пример показан на рис. П.1. Форма, размеры основной надписи и всех ее граф приведены на рис. П.2. Ðàìêà ïîëÿ ÷åðòåæà Ïîëå ïîäøèâêè ÷åðòåæà 5 s 20 s/2 5 55 5 185 Îñíîâíàÿ íàäïèñü Êðàé áóìàãè Ãðàíèöà ôîðìàòà Рис. П.1 185 23 15 10 11x5=55 2 1 10 11 12 13 3 70 Рис. П.2 34 15 17 18 5 6 7 20 8 9 50 15 5 15 5 15 7 10 В ГОСТ 2.104-68 описано назначение всех граф основной надписи и указан порядок их заполнения в производственных условиях: Графа 1 Графа 2 Графа 3 Графа 4 Графа 5 Графа 6 Графа 7 - Наименование детали или сборочной единицы. Обозначение документа. Обозначение материала детали. В этом задании графа не заполняется. Литера, присвоенная данному документу. Проставляется литера – у. Масса изделия. Не заполняется. Масштаб (см. ГОСТ 2.302-68 и ГОСТ 2.109-68). Порядковый номер листа (на документах, состоящих из одного листа, графу не заполняют). Графа 8 Общее количество листов документа (графу заполняют только на первом листе). Графа 9 Наименование предприятия (учебное заведение и номер группы). Графа 10 Характер работы, выполняемой лицом, подписывающим документ. Графа 11 Фамилии лиц, подписавших документ. Графа 12 Дата заполнения документа. Надписи, цифры и обозначения на чертеже должны быть выполнены чертежным шрифтом по ГОСТ 2.304-81 размером 3,5 и 5, а некоторые графы основной надписи ¾ размером 7 или 10. Все решения выполняются карандашом с помощью чертежных инструментов. Особое внимание должно быть обращено на тщательность графических построений. Небрежное выполнение построений неизбежно приводит к ошибочным результатам и к необходимости выполнения повторных решений задачи. Для большей точности построения вначале необходимо выполнить тонкими линиями твердым чертежным карандашом, а затем обвести более мягким. Начертание и толщина линий должны соответствовать требованиям ЕСКД. Рекомендуется толщина основных линий 0,8…1 мм, а линий связи и линий построений – 0,4…0,5 мм. Надписи, обозначения точек и цифровые индексы выполнять чертежным шрифтом с наклоном 75° в соответствии с ГОСТ 2.304-81. Содержание 1. Условные обозначения................................................................................................ 3 2. Точка, прямая, плоскость .......................................................................................... 4 3. Преобразование чертежа .......................................................................................... 20 4. Кривые поверхности ................................................................................................. 24 Приложение ................................................................................................................ 34 35