Реализация принципа системности и систематичности в

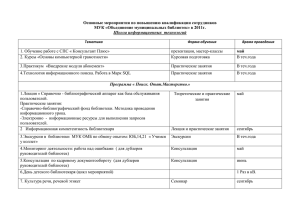
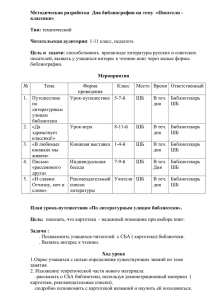
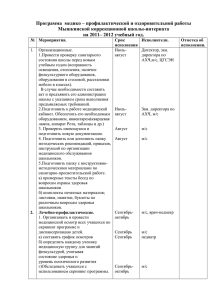
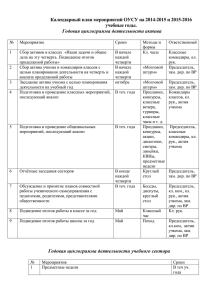
Смирнова Е.В.
МБОУ СОШ №3 с углубленным изучением отдельных предметов г.о. Самара
Реализация принципа системности и систематичности в компетентностно-контекстной модели обучения и воспитания при подготовке к ЕГЭ
В условиях традиционного обучения одним из дидактических принципов является «принцип систематичности и последовательности», который
предполагает усвоение знаний в определенной последовательности. Эта последовательность, как правило, в учебниках, учебных пособиях и изложении
учителя представляет собой линейное описание объектов и явлений, составляющих некоторую целостность. Предполагается, что в результате последовательного изучения такой совокупности объектов и явлений учащиеся
должны овладеть умениями распознавать систему в структуре изучаемой темы и предмета в целом. Однако, как показывает школьная практика, в сознании учащихся такая система не складывается, а изученные явления, объекты,
процессы остаются россыпью часто бесполезных фактов.
В компетентностно-контекстной модели обучения и воспитания, где на
первое место выходит умение использовать знания для решения проблем,
важное значение приобретает не столько последовательность, сколько системность знаний. Системность знаний характеризуется наличием в сознании
структурно-функциональных связей между разнородными элементами знаний. Это позволяет обучающимся не суммировать отдельно выхватываемые впечатления, а идти от целостного представления о некотором объекте
и лишь впоследствии приступать к рассмотрению, анализу его элементов,
вникать в подробности и использовать это знание для решения проблем. То
есть в компетентностно-контекстной модели обучения и воспитания через
принцип системности и систематичности реализуется принцип развивающего обучения «от общего к частному».
Покажем реализацию этого принципа на примере обучения решению
текстовых задач, которое занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей
уровня математического развития. Но по статистике решение задачи В13 в
ЕГЭ верное примерно у 70% учащихся.
Проследим на примере изучения темы «Решение задач» в курсе алгебры 8 класса, чем принцип «системности и систематичности» отличается от
принципа «систематичности и последовательности».
В учебнике Макарычева Ю.Н. Алгебра 8 кл. темы расположены в следующем порядке: Квадратное уравнение, Решение задач с помощью квадратных уравнений, Дробно-рациональные уравнения, Решение задач с помощью дробно-рациональных уравнений. Но ведь в КИМах и ГИА, и ЕГЭ
задачи не делятся по принципу, каким уравнением её решать. Квадратные и
дробно-рациональные уравнения – это всего лишь инструмент решения, и
решить уравнение в задаче не такая сложность, каким является процесс составления математической модели задачи. И именно это умение должно
чётко сформироваться у учащихся. Поэтому, целесообразно давать классификацию текстовых задач так, как представлено в прототипах В13, а не в
учебнике 8 класса. А именно, задачи на движение, работу и проценты.
И основным ключевым моментом в решении задач, является верное заполнение таблицы, в чём и заключается небольшая теория этой темы.
I
II
Разница (всего)
V(N)
T
S(A)
Для решения многих задач правильное заполнение таблицы – это уже
решенная задача, далее только нужно правильно решить квадратное или
дробно – рациональное уравнение, к которому сводится решение задачи.
Принципы заполнения таблицы рассматриваем на ключевых задачах.
Все ключевые задачи в структуре учащиеся решают в совместной деятельности с учителем. При этом учитель к каждой следующей задаче задает
один и тот же вопрос: задача какого типа и как будет выглядеть таблица?
Ключевые задачи.
1. Задачи на движение.
Движение по прямой дороге.
1)
При решении задач на равномерное движение часто встречаются две ситуации.
Если начальное расстояние между объектами равно S , а скорости объектов  1 и  2 , то:
а) при движении объектов навстречу друг другу время, через которое
они встретятся, равно
t
S
 1  2
б) при движении объектов в одну сторону ( 1   2 ) время, через которое
первый объект догонит второй, равно
t
S
 1  2
Движение по реке.
2)
Если объект движется по течению реки, то его скорость равна vпо
теч.=vсоб.
+vтеч.
Если объект движется против течения реки, то его скорость равна против vпо теч.=vсоб. -vтеч.
Собственная скорость объекта (скорость в неподвижной воде) равна
vсобс. 
vпо теч.  vпр.теч.
2
Скорость течения реки равна
vтеч. 
vпо теч.  vпр.теч.
2
Скорость движения плота равна скорости течения реки.
2. Задачи на работу.
Задачи на работу аналогичны задачам на движение. Вся работа играет
роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения.
1). Задачи на явную работу - задачи, в которых выполняемый объем работы известен или его нужно определить.
2). Задачи на неявную работу - задачи, в которых объем работы не указывается и не является искомым. Объем всей работы, который должен быть
выполнен, принимается за единицу.
3. Задачи на проценты и концентрацию.
В этой теме хорошо видна целостность, т.е. системность, а не последовательное изучение друг за другом отдельного типа задач, что позволяет
обучающимся не складывать в голове крупицы знаний о решении задач, а
использовать целостное представление о способах моделирования текстовых задач для решения широкого класса учебных задач и проблем.
Литература
1. Вербицкий, А. А. Методологические основы реализации новой образовательной парадигмы / А. А. Вербицкий, Н. А. Рыбакина // Педагогика. –
2014. – №2. – С. 3-14.
2. Рыбакина, Н. А. Компетеностно-контекстная модель обучения в общеобразовательной школе / Н. А. Рыбакина // Технологии построения систем
образования с заданными свойствами: материалы III Международной научно-практической конференции. – М. : РИЦ МГГУ им. М. А. Шолохова, 2013.