Лаб№4
реклама

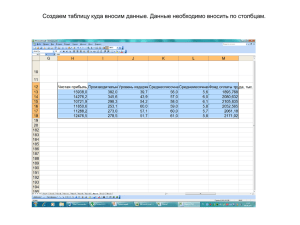
Лабораторная работа №4 Тема. Корреляционный и регрессионный анализы. Цель. Научить студента строить диаграмму рассеяния по таблице экспериментальных данных с использованием MS Excel. По данной диаграмме определять тип и форму корреляционной связи, определение уравнения регрессии (аппроксимирующей функции). Используя MS Excel находить значение коэффициента корреляции для простой регрессии. Находить уравнение регрессии и значение коэффициента детерминации. Часть 1. Для выборок, приведённых в таблицах, построить диаграмму рассеяния, определить тип и форму корреляционной зависимости, найти коэффициент корреляции. Объяснить выбор уравнения регрессии. Замечание. Отметим, что при построении диаграммы рассеяния требуется сделать сортировку по величине x (по той величине, значения которой наносятся ось абсцисс). Для построения диаграммы рассеяния использовать команду Вставка/График вместо команды Вставка/Точечная. Это позволит выбрать данные для оси абсцисс, так как по умолчанию по оси абсцисс указываются номера точек и, следовательно, теряется смысл задачи. Для определения коэффициента корреляции использовать функцию Коррел() в разделе Статистические функции на ленте Формулы. (см. рис. 1), предварительно выбрав ячейку для хранения (записи) результата вычисления функции. Рис. 1. После вызова функции КОРРЕЛ() появится окно Аргументы функции Рис. 2. Окно Аргументы функции КОРРЕЛ Вводим данные: Массив 1 значения первого признака x, и Массив2 – значения второго признака y (см. рис.). И щелкаем мышкой по кнопке ОК. Рис. 3. Окно Аргументы функции (данные введены) В выбранной ячейке отобразится значение коэффициента корреляции. Согласно нашему рисунку это значение равно 0,94 (0,939678464). Пример 1. Провести корреляционный анализ взаимосвязи роста (X) и массы (Y) наугад выбранных n=25 студентов. x i, y i, xi yi xi yi 185 170 183 183 163 188 77 66 75 77 68 82 173 180 178 183 188 193 82 84 100 84 84 70 185 175 165 178 188 178 76 83 66 67 95 63 185 165 185 74 61 77 183 175 183 79 77 70 Пример 2. Результаты тестирования (баллы) 10 студентов. Первый тест проверяет память x, второй – способность к логическому мышлению y. номер выборки 1 2 3 4 5 6 7 8 9 10 память, xi 5 8 7 10 4 7 9 6 8 6 логика, yi 7 9 6 9 6 7 10 7 6 8 Пример 3. На химическом производстве в ходе пяти рабочих смен получены следующие данные о зависимости выхода продуктов ξ2 (кг/час) от температуры ξ1 (0С): № 1 2 3 4 5 6 7 8 9 xi,(0C) 51 32 80 73 64 45 83 44 93 yi, (кг/час) 52,7 15,2 89,5 94,8 76 39,3 114,8 36,5 137,4 № 10 11 12 13 14 15 16 17 xi,(0C) 28 35 40 29 53 58 65 75 yi, (кг/час) 5,3 20,7 21,7 9,2 55,4 64,3 79,1 101 Пример 4. Таблица. Результаты подбрасывания двух кубиков: номер 1 подбрасывания 2 3 4 5 6 7 8 9 10 число очков, выпавшие на 4 1-м кубике, xi 6 5 1 1 5 1 5 6 6 число очков, выпавшие на 5 2-м кубике, yi 1 2 3 6 1 1 6 2 6 Пример 5. Задача взята из книги А.П. Матялис стр. 10 xi yi -0,667 2,6 -0,36 2,01 0,067 1,34 0,307 1,08 0,627 0,94 0,987 1,06 1,293 1,25 Часть 2. В данном разделе после корреляционного анализа требуется нанести на диаграммы рассеяния линии регрессии, предварительно обосновав выбор уравнения регрессии. Для построения линии регрессии выполним следующие действия: Щелкаем мышкой по графику (точки выделяются квадратиками); Нажимаем правую кнопку мышки (вызываем контекстное меню) и выбираем команду Добавить линию тренда. Появится окно Формат линии тренда (см. рис. ) Рис. 4. Окно "Формат линии тренда" Выбираем линию тренда, например, линейную. Обязательно ставим галочки в квадратики "Показывать уравнение на диаграмме" и "Поместить на диаграмму величину достоверности аппроксимации" (см. рис. ). Рис. Выбор линии тренда (линейная) Диаграмма рассеяния и линия регресии 5 4.5 4 3.5 3 2.5 2 y = 0,2461x + 2,0467 R² = 0,9049 1.5 1 0.5 0 55 60 70 75 80 85 95 100 110 120 Что обозначает величина R2? Это величина носит название коэффициента детерминации и показывает вклад аргумента x в значение функции y. В нашем случае R2=0,905. В нашем случае вклад аргумента равен 0,905, т.е. 90,5%, а остальное не учтённые факторы, в частности – случайные факторы, например, погрешности измерения. В линейной модели величина R (корень квадратный из R2) есть коэффициент корреляции взятый со знаком коэффициента при x. Заметим, что коэффициент корреляции характеризует тесноту линейной зависимости между переменными, в случае нелинейной зависимости следует пользоваться коэффициента детерминации.