Показательные и логарифмические функции
реклама
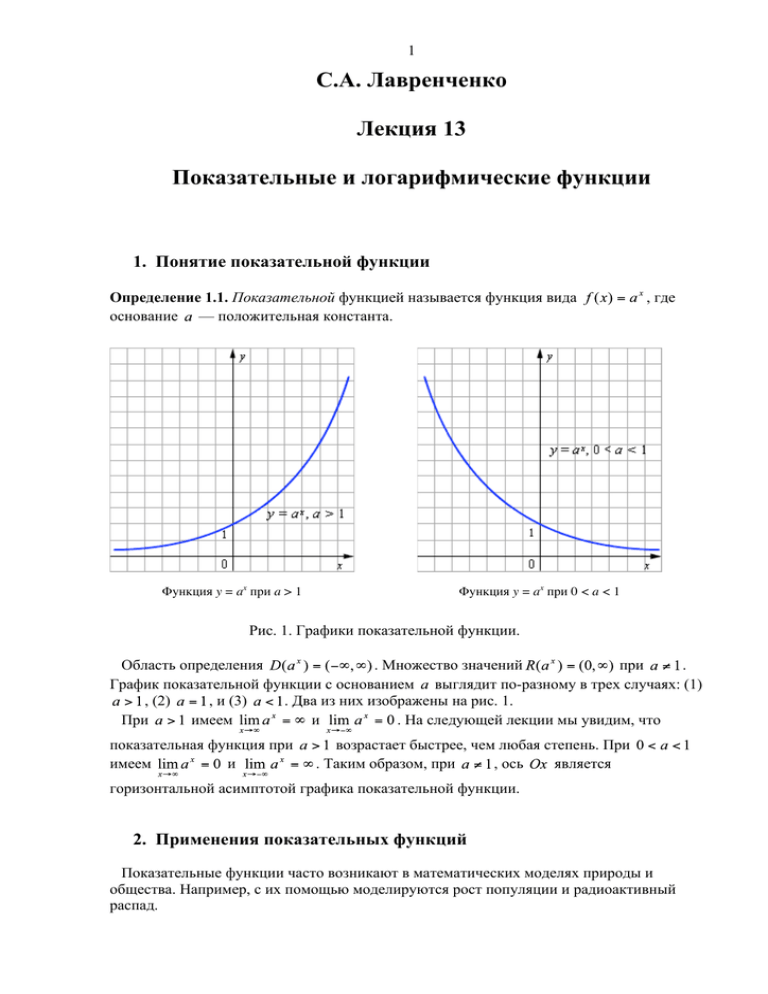
1 С.А. Лавренченко Лекция 13 Показательные и логарифмические функции 1. Понятие показательной функции Определение 1.1. Показательной функцией называется функция вида основание — положительная константа. Функция y = ax при a > 1 , где Функция y = ax при 0 < a < 1 Рис. 1. Графики показательной функции. Область определения . Множество значений при . График показательной функции с основанием выглядит по-разному в трех случаях: (1) , (2) , и (3) . Два из них изображены на рис. 1. При имеем и . На следующей лекции мы увидим, что показательная функция при имеем и возрастает быстрее, чем любая степень. При . Таким образом, при , ось является горизонтальной асимптотой графика показательной функции. 2. Применения показательных функций Показательные функции часто возникают в математических моделях природы и общества. Например, с их помощью моделируются рост популяции и радиоактивный распад. 2 Пример 2.1. — численность популяции бактерий через часов. Пример 2.2. Изотоп стронция является радиоактивным с периодом полураспада 28,79 лет. Таким образом, если начальная масса некоторого количества стронция-90 равна, например, 24 миллиграмма, то масса остающегося через лет количества будет равна мг. ( образуется при ядерных взрывах и выбросах с АЭС.) 3. Число е Определение 3.1. Число определяется так: . В 3-м семестре будет доказано, что этот предел существует. Студентам рекомендуется поработать с научным калькулятором, вычисляя значения выражения , при , и убедиться что эти значения стабилизируются около некоторого определенного значения, которое и называется числом . Это иррациональное число; оно представляется бесконечной непериодической десятичной дробью. Вычисления показывают, что . Если в определении числа сделать замену , получим эквивалентное определение: . 4. Второй замечательный предел Мы скоро увидим, что показательная функция при играет особо важную роль. Она называется экспонентой и имеет специальное обозначение: . Таким образом, . Теорема 4.1 (второй замечательный предел). Доказательство: нулю. Следовательно, . , причем эта аппроксимация тем точнее, чем ближе , и в пределе при получится доказываемое равенство. ■ 5. Производная экспоненты к 3 Особая роль и исключительность функции обуславливается следующей теоремой. Теорема 5.1 (производная экспоненты). Производная экспоненты равна ей самой, т.е. . Доказательство: Используем определение производной и второй замечательный предел: .■ Следствие 5.2. .■ 6. Логарифмические функции Показательная функция монотонно убывает при она имеет обратную при строго монотонно возрастает при , и строго . Значит, по теореме о существовании обратной функции, . Определение 6.1. Функция, обратная к показательной функции называется логарифмической функцией по основанию и обозначается . Область определения при , т.е. и множество значений . Рис. 2. Графики логарифмической функции. Графики логарифмической функции получаются из соответствующих графиков показательной функции зеркальным отражением относительно прямой . Кривые при любом ( ) непрерывны и проходят через точку . На следующей лекции мы увидим, что при логарифмическая функция возрастает медленнее, чем любая степень. При имеем и . Таким образом, ось является вертикальной асимптотой графика логарифма. По определению обратной функции, тогда и только тогда, когда , где , и . Таким образом, логарифм числа по основанию есть показатель, в который надо возвести основание , чтобы получить . Законы сокращения для показательной и логарифмической функций выглядят так: для всех ,и для всех . 4 Часто используется логарифмы по основанию . Они называются десятичными логарифмами и обозначаются , т.е. . Еще более важны логарифмы по основанию , к изучению которых мы сейчас переходим. 7. Натуральные логарифмы Наиболее удобным основанием логарифма служит число . Определение 7.1. Логарифм числа натуральным логарифмом, т.е. Например, , по основанию . обозначается . Теорема 7.2 (производная натурального логарифма). Доказательство: Запишем закон сокращения . Получаем: . и продифференцируем обе части по , откуда Следствие 7.3. Пример 7.4. Найти и называется .■ .■ . Решение: .■ Пример 7.5. Продифференцировать функцию Решение: Пример 7.6. Найти производную . .■ . Решение: .■ Теорема 7.7 (производная логарифма модуля). при Доказательство: По определению модуля имеем . . 5 Если , имеем . Если же , получается тот же результат: .■ 8. Производные общих логарифмических и показательных функций Теорема 8.1 (производная общей логарифмической функции). Доказательство: . .■ Теорема 8.2 (производная общей показательной функции). . Доказательство: . Заметим, что формула справедлива и при .■ 9. Логарифмическое дифференцирование Логарифмическое дифференцирование — это метод дифференцирования функции , состоящий из следующих трех шагов. Шаг 1: Взять натуральные логарифмы от обеих частей равенства Шаг 2: Продифференцировать обе части по . При этом Шаг 3: Решить получающееся уравнение относительно Замечание 9.1. Если для некоторых этом случае, пишем . . . , то логарифм и используем формулу не определен. В из теоремы 7.7. Этим методом докажем сейчас правило дифференцирования степени с произвольным действительным показателем. Теорема 9.2 (производная степени). Пусть Тогда . Доказательство: Записываем функцию как , откуда — произвольное действительное число. , откуда , откуда , если считать внешней функцией логарифм 6 модуля, а внутренней функцией — функцию . Окончательно, .■ Логарифмическое дифференцирование предоставляет возможность дифференцировать функции, в выражении которых независимая переменная фигурирует как в основании степени, так и в ее показателе. Такие функции ни степенные, ни показательные, и у нас нет готовой формулы для их вычисления. Пример 9.3. Продифференцировать функцию . Решение: Берем логарифмы от обеих частей: части: . Дифференцируем обе . Упрощая и разрешая относительно и, окончательно, , получаем .■ Упражнения для самопроверки 1. Изобразить график показательной функции с основанием . 2. Доказать следствие 5.2. 3. Найти пределы и при необходимо рассматривать односторонним? 4. Доказать следствие 7.3. . Почему второй предел