Лабораторная работа № 2.24 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА
реклама

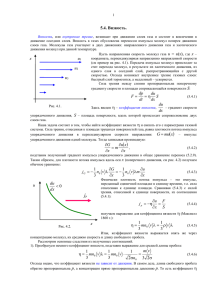
Лабораторная работа № 2.24 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА И СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ АЗОТА. Принадлежности: установка для определения вязкости воздуха, секундомер. Цель работы: экспериментальное определение коэффициента вязкости воздуха, средней длины свободного пробега и эффективного диаметра молекул азота. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ Вязкость или внутреннее трение — свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. При течении газа вдоль трубы скорости разных слоев распределены так, как показано на рис. 1, где стрелки представляют векторы скоростей u слоев, перпендикулярные оси х. Наибольшая скорость наблюдается в средней прилегающей к оси части трубы, по мере приближения к стенкам скорость уменьшается, а слой, непосредственно прилегающий к стенкам трубы, неподвижен. В результате теплового движения молекулы газа переходят из одного слоя в другой, перенося при этом свой импульс mu упорядоченного движения. В результате обмена молекулами между слоями, движущимися с различными скоростями, импульс упорядоченного движения быстрее движущегося слоя Рис. 1 уменьшается, а медленнее движущегося слоя – 1. увеличивается. Другими словами, быстрее движущийся слой тормозится, а медленнее движущийся – ускоряется. Согласно второму закону Ньютона сила равна быстроте изменения импульса, т.е. производной импульса по времени. Это значит, что на каждый из слоев, движущийся относительно соседнего, действует сила, равная изменению импульса в единицу времени. Сила эта – сила трения между слоями газа, движущимися с различными скоростями. Отсюда и название – внутреннее трение. Уравнение для силы внутреннего трения между соседними слоями называется законом Ньютона: F du S. dx (1) Здесь η – динамическая вязкость, S – площадь поверхности, лежащей на границе между слоями, du/dx – быстрота изменения скорости течения жидкости или газа в направлении х, перпендикулярном к направлению движения слоев (градиент u). В молекулярно-кинетической теории доказывается, что вязкость и средняя длина свободного пробега молекулы связаны выражением: 3 =. 8M p RT (2) где р - давление газа (определяется барометром), М – молярная масса газа (для азота M = 28 10 -3 кг/моль), R = 8,31 Дж/(К моль) - газовая постоянная, T абсолютная температура, Т = 273 + tº C (определяется термометром). Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называют эффективным диаметром молекул dэфф.. Его можно определить из выражения для средней длины свободного пробега kT (3) 2 2d эф p k = 1,38·10-23Дж/К – постоянная Больцмана. Из (3) имеем d эф kT . 2p (4) Воздух примерно на 80% состоит из азота, поэтому используя значение вязкости воздуха, можно определить среднюю длину свободного пробега и эффективный диаметр молекул азота. Суть применяемого в данной работе метода определения вязкости состоит в том, что газ (воздух) прокачивают через тонкую цилиндрическую тру6ку (капилляр). Чем больше вязкость газа, тем с меньшей скоростью он будет проходить через тонкое отверстие капилляра, и тем меньше объем газа, прошедшего за единицу времени через капилляр. Описание установки Вязкость воздуха определяется с помощью установки, изображенной на рис. 2, где 1 – аспиратор (процесс отбора газа называется аспирацией), 2 – манометр, 3 – капилляр, 4, 5 – краны, 6 - пробка, 7 – шкала аспиратора. Чтобы определить вязкость, воздух пропускают через капилляр 3. Это можно осуществить с помощью аспиратора 1. Если открыть кран 4, то вода будет выливаться из аспиратора, а над поверхностью воды в аспираторе создается пониженное давление воздуха. Вследствие этого концы капилляра 3 находятся под разными давлениями. Давление у нижнего открытого конца равно атмосферному, у верхнего – пониженное, как в аспираторе, с которым капилляр соединен трубкой. Разность давлений способствует всасыванию воздуха в аспиратор через капилляр. Эту разность давлений измеряют с помощью манометра 2, одно колено которого открыто (атмосферное давление), а другое соединено с аспиратором (пониженное давление). Объём воздуха, прошедшего через капилляр за определённое время, равен объёму воды, вытекшей из аспиратора. Объем вытекшей воды измеряется по шкале на аспираторе. Согласно формуле Пуазейля вязкость газа, проходящего через капилляр, прямо пропорциональна разности давлений р у входа в капилляр и на выходе из него и обратно пропорциональна объему V газа, протекающему через капилляр за промежуток времени Δt: r 4 p t 8 V L , где r - радиус капилляра, L - его длина. Разность давлений у входа и выхода капилляра равна p в g h , (5) (6) где ρв = 1000 кг/мз - плотность воды в манометре, g = 9,81м/с2 - ускорение свободного падения, Δh - средняя разность уровней жидкости в коленах манометра. С учетом (11) итоговая формула для расчета вязкости воздуха имеет вид: r 4 в g h t . (7) 8 V L Порядок выполнения работы Задание 1. Определение вязкости воздуха. 1. Открыть кран 5, вынуть пробку 6, наполнить аспиратор на 3/4 водой, затем закрыть кран 5 и поставить на прежнее место пробку 6. 2.Открыть кран 4 и, дождаться, когда вода начнёт вытекать из аспиратора редкими каплями, а уровни воды в коленах манометра прекратят движение, после этого измерить разность уровней воды в коленах манометра h1 . 3.Включить секундомер и определить промежуток времени Δt , за который из аспиратора вытечет определённый объём воды V. Столько же времени воздух протекал через капилляр. Объём вытекшей воды измерить по шкале на аспираторе. 4. Измерить по шкале манометра конечную разность уровней воды в коленах Δh2. 5. Вычислить среднюю разность уровней h воды в коленах манометра по формуле h1 h2 . (8) 2 6. Вычислить вязкость воздуха по формуле (7). Длина и радиус капилляра указаны на приборе. Опыт повторить 5 раз. Результаты измерений и вычислений занести в таблицу. Окончательный результат записать в виде , Па с при =... h Задание 2. Определение средней длины свободного пробега и эффективного диаметра молекул азота. 7. Измерить температуру t˚ воздуха термометром и атмосферное давление p барометром. 8. Зная вычисленное среднее значение вязкости , по формуле (2) определить среднюю длину свободного пробега молекул λ, результаты занести в таблицу. 9. По формуле (4) определить эффективный диаметр молекул азота, результаты занести в таблицу. Таблица N Δh1, м Δh2, Δh, м м V м3 Δt, с η, <η> Δη Па∙с Па∙с Па∙с E, % T, К P, Па λ, м dэфф, м 1. 2. 3. 4. 5. Контрольные вопросы. 1.Каков механизм возникновения сил вязкого трения в газе? Что называется вязкостью газа? 2.В чем суть данного метода определения вязкости воздуха? 3.Каким способом создается разность давлений на концах капилляра, через который прокачивается воздух? 4.Что называется средней длиной свободного пробега молекул? 5.Что называется эффективным диаметром молекул?