50 С развитием технологий производители компьютеров
реклама
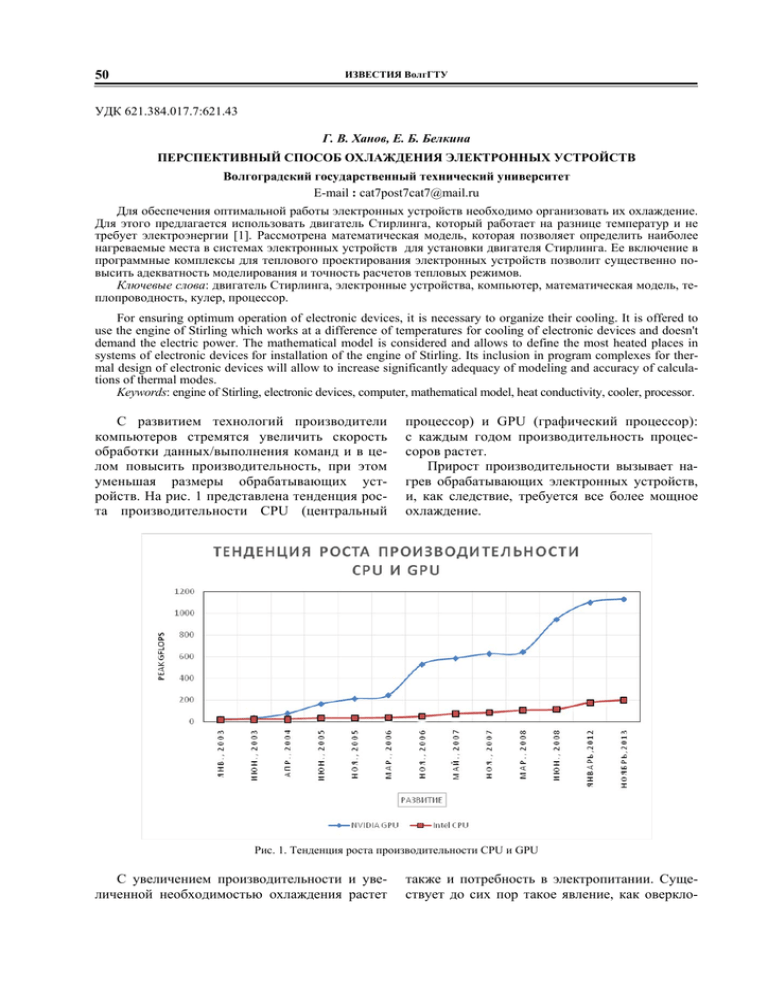
50 ИЗВЕСТИЯ ВолгГТУ УДК 621.384.017.7:621.43 Г. В. Ханов, Е. Б. Белкина ПЕРСПЕКТИВНЫЙ СПОСОБ ОХЛАЖДЕНИЯ ЭЛЕКТРОННЫХ УСТРОЙСТВ Волгоградский государственный технический университет E-mail : cat7post7cat7@mail.ru Для обеспечения оптимальной работы электронных устройств необходимо организовать их охлаждение. Для этого предлагается использовать двигатель Стирлинга, который работает на разнице температур и не требует электроэнергии [1]. Рассмотрена математическая модель, которая позволяет определить наиболее нагреваемые места в системах электронных устройств для установки двигателя Стирлинга. Ее включение в программные комплексы для теплового проектирования электронных устройств позволит существенно повысить адекватность моделирования и точность расчетов тепловых режимов. Ключевые слова: двигатель Стирлинга, электронные устройства, компьютер, математическая модель, теплопроводность, кулер, процессор. For ensuring optimum operation of electronic devices, it is necessary to organize their cooling. It is offered to use the engine of Stirling which works at a difference of temperatures for cooling of electronic devices and doesn't demand the electric power. The mathematical model is considered and allows to define the most heated places in systems of electronic devices for installation of the engine of Stirling. Its inclusion in program complexes for thermal design of electronic devices will allow to increase significantly adequacy of modeling and accuracy of calculations of thermal modes. Keywords: engine of Stirling, electronic devices, computer, mathematical model, heat conductivity, cooler, processor. С развитием технологий производители компьютеров стремятся увеличить скорость обработки данных/выполнения команд и в целом повысить производительность, при этом уменьшая размеры обрабатывающих устройств. На рис. 1 представлена тенденция роста производительности CPU (центральный процессор) и GPU (графический процессор): с каждым годом производительность процессоров растет. Прирост производительности вызывает нагрев обрабатывающих электронных устройств, и, как следствие, требуется все более мощное охлаждение. Рис. 1. Тенденция роста производительности CPU и GPU С увеличением производительности и увеличенной необходимостью охлаждения растет также и потребность в электропитании. Существует до сих пор такое явление, как оверкло- 51 ИЗВЕСТИЯ ВолгГТУ кинг, который актуален несмотря на тенденцию снижения энергопотребления процессоров. Разгон процессора (оверклокинг) возможен только в случае его эффективного охлаждения. При разгоне процессора нужно использовать очень эффективную систему охлаждения. А для мощных суперкомпьютеров необходимость в охлаждении очень перспективна. Для дата-центров, например, уже несколько лет подряд остро сто- ит вопрос их охлаждения и снижения энергопотребления при этом. Предлагается для охлаждения использовать систему жидкостного охлаждения с применением двигателя Стирлинга, который работает на разнице температур и не требует никакой электроэнергии. Вместе с тем, он выступает как теплообменник. На рис. 2 представлена общая схема жидкостного охлаждения мощного компьютера. Теплообменник Рис. 2. Общая схема жидкостного охлаждения компьютера Одним из основных механизмов теплообмена в двигателе Стирлинга является конвективный теплообмен, поэтому его адекватное математическое моделирование необходимо как для практики теплового проектирования электронных устройств, так и для включения адекватных моделей в САПР моделирования тепловых режимов. Рассмотрев тепловые потоки, которые передаются на двигатель Стирлинга, и рассмотрев цикл Стирлинга, определим термический КПД для нормальных условий для различной подведенной теплоты (см. таблицу). Количество подведенной теплоты Q01, Дж Объем V0, л Температура T0, К Атмосферное давление, p0, атм Термический КПД, η 50 22,4 273,159 1 0,015 100 22,4 273,159 1 0,029 550 22,4 273,159 1 0,128 1000 22,4 273,159 1 0,227 10000 22,4 273,159 1 0,746 Из таблицы видно, что термический КПД двигателя Стирлинга повышается при увеличении подаваемого количества теплоты на двигатель [3]. Важно также определить в системе охлаждения электронных устройств оптимальное место для установки двигателя. Протекание конвективных процессов теплообмена опреде- ляется влиянием множества факторов, таких как геометрические размеры электронного устройства, его конструктивные особенности, герметичность устройства, наличие вентиляционных отверстий, пространственное расположение элементов внутри устройства, характер ограниченности пространства и пр. Поэтому, 52 ИЗВЕСТИЯ ВолгГТУ когда конвективный теплообмен происходит в замкнутом пространстве в математическую модель сопряженного теплообмена, необходимо вводить соответствующие уравнения теплопроводности и граничные условия 4-го рода. В общем виде система уравнений, описывающая стационарный свободный конвективный теплоперенос около твердого тела, относительно малых переменных температурного поля T¢ и поля давления в жидкости p¢, имеет вид: p (v)v= gT+vv, vT=aT, (1) divv=, w Tw Q(x,y,x)=. Система включает в себя: уравнения Навье– Стокса, уравнения переноса энергии, уравнения непрерывности и уравнения теплопроводности в твердом теле (ω) с пространственным распределением источников теплоты Q(x, y, z). К системе необходимо добавить граничные условия 4-го рода на границе тела и газа ∂S: T T w w (2) , ri aS n aS где T = T0+T¢, p = p0+p¢, T0 и p0 – постоянные средние значения температуры и давления в газах, от которых отсчитываются неравномерности температуры T¢ и давления p¢ [4]; T¢ и v – трехмерные поля температуры и скорости в газах; T – трехмерное температурное поле в теле; ν – кинематическая вязкость воздуха; a = λ/ρc – температуропроводность воздуха теплопроводностью λ, плотностью ρ и удельной теплоемко- стью c; β – температурный коэффициент расширения воздуха; – теплопроводность материала тела; g – ускорение свободного падения; n – нормаль к поверхности тела. Предлагаемая математическая модель довольно сложна, но вместе с тем она наиболее адекватно описывает конвективные процессы в реальных электронных системах и позволяет определить наиболее нагреваемые места в системах электронных устройств для установки двигателя Стирлинга. Таким образом, предлагаемый способ охлаждения электронных устройств с целью снижения энергопотребления с применением двигателя Стирлинга является наиболее перспективным. Решения предлагаемой математической модели и включение ее в программные комплексы для теплового проектирования электронных устройств позволит существенно повысить адекватность моделирования и точность расчетов тепловых режимов. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Белкина, Е. Б. Разработка теплообменного аппарата для охлаждения процессоров в компьютере / Е. Б. Белкина, Г. В. Ханов // Городу Камышину –- творческую молодежь : матер. IV регион. науч.-практ. студенческой конф., г. Камышин, 14–16 апр. 2010 г. В 7 т. Т. 6 / КТИ (филиал) ВолгГТУ. – Волгоград, 2010. – C. 30–32. 2. Ханов, Г. В. Альтернативный способ охлаждения процессоров в компьютере / Г. В. Ханов, Е. Б. Белкина // Экология и жизнь : сб. ст. XVIII междунар. науч.-практ. конф., апрель 2010 г. / Приволжский Дом знаний [и др.]. – Пенза, 2010. – C. 137–139. 3. Ханов, Г. В. Методика расчета энергопреобразующей системы на основе двигателя Стирлинга, установленного на процессор компьютера / Г. В. Ханов, Е. Б. Белкина // Современные технологии в машиностроении : сб. ст. XIV Междунар. науч.-практ. конф. (декабрь 2010 г.) / Приволжский Дом знаний [и др.]. – Пенза, 2010. – C. 390–393. УДК 658.512 ; 519.246 Ю. Л. Чигиринский, Н. В. Чигиринская, Л. А. Качалова МНОГОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ В MATHCAD Волгоградский государственный технический университет E-mail: techmash@vsti.ru, jilio-tchigirinsky@yandex.ru Обоснована возможность проведения регрессионного анализа экспериментальных данных с использованием инструментальных средств систем компьютерной алгебры. Предложена структура документа MathCAD, позволяющая компактно представить расчеты, связанные с определением параметров регрессионных моделей трех основных спецификаций: линейной, степенной и показательной. Предусмотрена возможность оценки и сравнения погрешностей моделирования и достоверности получаемых моделей. Ключевые слова: регрессионная модель, система компьютерной алгебры, многофакторная модель, достоверность моделирования, правила Гаусса–Маркова. Substantiated the possibility of conducting a regression analysis of experimental data using the tools of CAS. Proposed the structure of MathCAD worksheet that allows to compactly represent the calculations associated with determining the parameters of the regression models of the three main specifications: linear, power and exponential. Is possibility of evaluation and comparison of modeling errors and the reliability of the obtained models. Keywords: regression model, Computer Algebra System (CAS), multifactor model, simulation accuracy, Gauss– Markov conditions.




