СПОСОБЫ НАБЛЮДЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА Зеркала
реклама
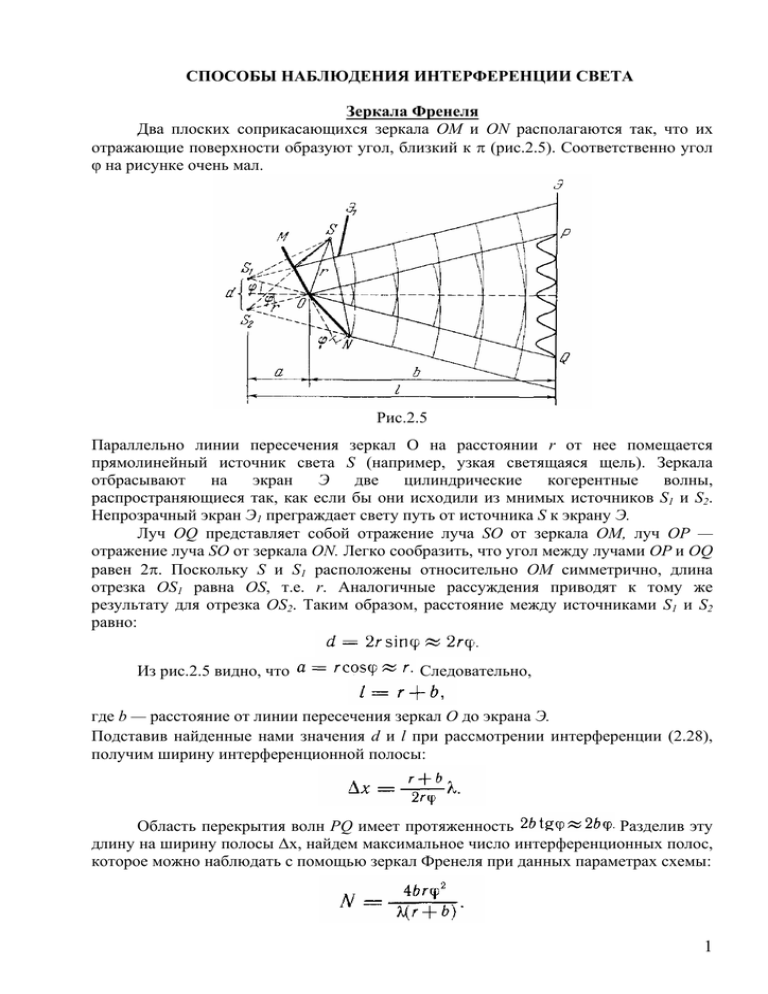
СПОСОБЫ НАБЛЮДЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА Зеркала Френеля Два плоских соприкасающихся зеркала ОМ и ON располагаются так, что их отражающие поверхности образуют угол, близкий к π (рис.2.5). Соответственно угол φ на рисунке очень мал. Рис.2.5 Параллельно линии пересечения зеркал О на расстоянии r от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S1 и S2. Непрозрачный экран Э1 преграждает свету путь от источника S к экрану Э. Луч OQ представляет собой отражение луча SO от зеркала ОМ, луч ОР — отражение луча SO от зеркала ON. Легко сообразить, что угол между лучами ОР и OQ равен 2π. Поскольку S и S1 расположены относительно ОМ симметрично, длина отрезка OS1 равна OS, т.е. r. Аналогичные рассуждения приводят к тому же результату для отрезка OS2. Таким образом, расстояние между источниками S1 и S2 равно: Из рис.2.5 видно, что Следовательно, где b — расстояние от линии пересечения зеркал О до экрана Э. Подставив найденные нами значения d и l при рассмотрении интерференции (2.28), получим ширину интерференционной полосы: Разделив эту Область перекрытия волн PQ имеет протяженность длину на ширину полосы ∆х, найдем максимальное число интерференционных полос, которое можно наблюдать с помощью зеркал Френеля при данных параметрах схемы: 1 Бипризма Френеля Изготовленные из одного куска стекла две призмы с малым преломляющим углом υ имеют одну общую грань (рис.2.6) Параллельно этой грани на расстоянии а от нее располагается прямолинейный источник света S. Рис.2.6 Можно показать, что в случае, когда преломляющий луч υ призмы очень мал и углы падения лучей на грань призмы не очень велики, все лучи отклоняются призмой на практически одинаковый угол, равный: (п—показатель преломления призмы). Угол падения лучей на бипризму невелик. Поэтому все лучи отклоняются каждой из половин бипризмы на одинаковый угол. В результате образуются две когерентные волны, исходящие из мнимых источников S1 и S2, лежащих в одной плоскости с S. Расстояние между источниками равно: Расстояние от источников до экрана: Ширину интерференционной полосы находим по формуле: Область перекрытия волн PQ имеет протяженность: Максимальное число наблюдаемых полос: Кольца Ньютона Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной толстой стеклянной пластинки и плосковыпуклой линзы с 2 большим радиусом кривизны (рис.2.7). Рис.2.7 Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении — эллипсов. Найдем радиусы колец Ньютона, получающихся при падении света по и оптическая разность хода равна нормали к пластинке. В этом случае удвоенной толщине зазора. Из рис.2.7 следует, что (2.29) где R — радиус кривизны линзы, r — радиус окружности, всем точкам которой соответствует одинаковый зазор b. Ввиду малости b мы пренебрегли величиной b2 по сравнению с 2Rb. В соответствии с (2.29): Чтобы учесть возникающее при отражении от пластинки изменение фазы на прибавить . В результате получится: π, нужно к В точках, для которых для которых условия можно объединить в одно: (2.30) , возникнут максимумы, в точках, , – минимумы интенсивности. Оба причем четным значениям m будут соответствовать максимумы, а нечетным – минимумы интенсивности. Подставив сюда выражение для ∆ (2.30) и разрешив получившееся уравнение относительно r, найдем радиусы светлых и темных колец Ньютона: Четным m соответствуют радиусы светлых колец, нечетным m – радиусы темных колец. Значению m = 1 соответствует r == 0, т.е. точка в месте касания пластинки и линзы. В этой точке наблюдается минимум интенсивности, обусловленный изменением фазы на π при отражении световой волны от пластинки. 3