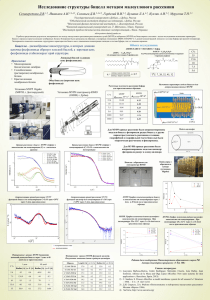
Лопушенко И.В.

Гибридная схема метода дискретных источников в задачах рассеяния световых
волн частицами на подложке
Лопушенко Иван Владимирович
Студент
Московский государственный университет имени М.В.Ломоносова,
физический факультет, Москва, Россия
E-mail: lopushenko.ivan@physics.msu.ru
Развитие современных технологий и расширение сферы применимости
металлических и диэлектрических наноструктур в различных прикладных задачах
приводит к тому, что необходимо корректно анализировать рассеивающие свойства
различных наночастиц, а так же их систем [1]. Особенный интерес вызывают
наночастицы из благородных металлов, таких как серебро (Ag) или золото (Au) в силу
своих уникальных оптических свойств в видимом диапазоне длин волн. Проявление
этих свойств связано с явлением локализованного поверхностного плазмонного
резонанса (англ. LSPR — Localized Surface Plasmon Resonance). Это явление
наблюдается при облучении светом металлической наночастицы, характерный размер
которой меньше длины свободного пробега электрона в металле, и заключается в резком
росте амплитуды электромагнитного поля вблизи наночастицы на несколько порядков
по сравнению с внешним возбуждением [2]. Зависимость свойств LSPR от формы и
показателя преломления наночастицы даёт возможность контролировать усиление
электромагнитного поля на масштабах, меньших длины волны внешнего возбуждения,
которая успешно применяется в таких прикладных эффектах, как комбинационное
рассеяние света (англ. SERS — Surface-Enhanced Raman Scattering), а так же при
разработке современных оптических наноантенн и биосенсоров. В связи с этим
актуальной задачей является построение строгой математической модели,
предназначенной для решения подобных задач. В данной работе предлагается гибридная
схема метода дискретных источников (МДИ) для анализа рассеяния световых волн
проницаемыми наночастицами, расположенными на подложке.
Задача дифракции плоской линейно поляризованной волны {E0 ,H0} на локальном
объекте в слоистой среде [2] формулируется в нашем случае следующим образом. Пусть
задана среда с двумя однородными изотропными слоями D0,1 , плоскостью границы
раздела  , и однородной проницаемой частицей Di с гладкой границей Di  C 2 вблизи 
в верхнем полупространстве D0 . Полагая все необходимые параметры системы
известными и вводя цилиндрическую систему координат (  ,  , z ) , в которой ось z
направлена перпендикулярно границе раздела полупространств {  : z  0 } в D0 ,
математическую постановку задачи рассеяния плоской волны {E0 ,H0} , падающей под
углом   0 относительно оси z на частицу Di , можно записать в виде:
rot H   jk  E ;
rot E   jk H  (в D ,   0,1, i ),
n p  Ei ( p)  E0 ( p)  0,
e z  E 0 ( p )  E1 ( p )   0,
p ;
(1)
p  Di ;
n p  H i ( p)  H 0 ( p)  0,
e z  H 0 ( p )  H1 ( p )   0,
r


lim r    0 E 0s    0 H 0s   0, r  M  , z  0;
r


r 
( E1s , H1s )   (exp{ Im k1 r}),
Здесь
поле,
np
{E ,H }
z  0.
 полное поле в соответствующей области
 единичная нормаль к поверхности Di ,
соответствующего
полупространства
D
,
а
D
k       
параметры
,
{Es , Hs }
 рассеянное
, M – некоторая точка
сред
удовлетворяют
соотношениям Im 0 , 0  0, Im1, 1  0 . Поставленная граничная задача (1) имеет
единственное решение. Временная зависимость выбирается в виде exp( jt ) .
В основу разрабатываемой математической модели для решения поставленной
задачи положена гибридная схема метода дискретных источников (МДИ, или DSM —
Discrete Sources Method). Её суть состоит в том, что рассеянное поле {Es , H s } всюду вне
объекта Di можно представить в виде конечной линейной комбинации полей дипольных
дискретных источников (ДИ), распределённых внутри объекта. Поля ДИ строятся на
основе тензора Грина полупространства. Такое выражение для рассеянного поля
аналитически удовлетворяет уравнениям Максвелла, условиям на бесконечности и
условиям сопряжения на границе раздела сред  . Таким образом, для решения задачи
дифракции (1) необходимо определить неизвестные амплитуды ДИ, аппроксимируя
условия сопряжения полей на поверхности тела Di [1]. Особенности данного метода
заключаются в том, что в качестве ДИ выбираются электрические и магнитные диполи,
распределённые вдоль линии внутри частицы, а представление для рассеянного поля не
зависит от типа линейной поляризации плоской волны. Кроме того, преимуществами
данного метода являются возможность эффективно проводить соответствующие
расчёты для наночастиц произвольной формы, осуществлять апостериорную оценку
погрешности полученного результата, а так же низкие требования к вычислительным
операциям.
Амплитуды ДИ определяются с помощью обобщённого метода коллокаций, который
приводит к переопределённой системе уравнений [2]. Решение такой системы ищется в
норме l2 на поверхности частицы методами минимизации невязки, а вычисление
значения поверхностной невязки выполнения граничных условий на другом наборе
точек коллокаций даёт апостериорную оценку погрешности приближённого решения.
Физическим результатом решения исходной задачи является диаграмма рассеяния
F( ,  ) в верхнем полупространстве:
E(r) E0 (r) 
exp{ jk 0 r}
F( , )  O(1 r 2 ),
r
r  , z  0
(2)
В случае расчётов с помощью МДИ математическое представление F( ,  ) сводится
к конечной линейной комбинации элементарных функций [1], что позволяет избежать
процедуры интегрирования и обеспечивает низкие вычислительные затраты на
исследование характеристик рассеяния, одной из которых является дифференциальное
сечение рассеяния (англ. DSC — Differential Scattering Cross-Section), характеризующее
интенсивность рассеяния:
2
DSC( 0 , , )  F ( 0 , , )  F ( 0 , , )
2
Полученные в ходе моделирования результаты для дифракции плоской линейно
поляризованной волны на металлических и диэлектрических наночастицах в среде с
рассмотренной выше конфигурацией будут представлены в ходе презентации.
Литература
1. Ерёмин Ю.А., Свешников А.Г. Математические модели задач нанооптики и
биофотоники на основе метода дискретных источников //Журн. вычисл. матем. и
матем. физ., 47:2 (2007), стр. 269–287
2. Лопушенко И.В. Исследование влияния подложки на рассеивающие свойства
проницаемых частиц //Акустооптические и радиолокационные методы измерений и
обработки информации: Материалы 6-й Международной научно-технической
конференции ARMIMP-2013, стр. 79.