Ю.Г. Дёмина (студент), А.С. Орлов (кандидат технических наук, доцент)

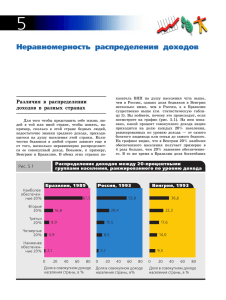
Ю.Г. Дёмина (студент), А.С. Орлов (кандидат технических наук, доцент)
КРИВАЯ ЛОРЕНЦА И КОЭФФИЦИЕНТ ДЖИНИ –
ПОСТРОЕНИЕ ЭКОНОМИЧЕСКОЙ МОДЕЛИ В MS EXCEL
Великий Новгород, РГУИТП СФ
В России за последние десятилетия проблемы неравенства стали
предметом
активных
общественных
дискуссий,
ведущихся
экономистами, социологами и представителями других наук [2].
Неравенство
доходов
и
богатства
является
источником
социальной нестабильности.
Доходы и покупательная способность населения определяют не
только
уровень
жизни,
но
и
емкость
внутреннего
рынка,
обуславливающую экономическое развитие страны. Это значит, что
для благоприятного развития экономики России особое внимание стоит
уделить повышению доходов наиболее бедной и средней части
населения.
Неслучайно
сегодня
впервые
социальная
сфера
рассматривается не как способ смягчить последствия кризиса, а
становится
приоритетом,
призванным
обеспечить
максимизацию
инвестиций в человеческий капитал. Никогда раньше в программах
российского правительства и даже в Советском Союзе социальный
раздел не был первым по очерёдности. Именно это и обосновывает
актуальность рассмотрения данной темы.
Назрела острая необходимость исследования перераспределения
денежных доходов, их анализа по тем или иным группам населения
Российской Федерации.
Важнейшим инструментом анализа социально-экономической
дифференциации
населения
является
построение
распределения
населения по уровню среднедушевого денежного дохода, что позволяет
проводить сравнительную оценку благосостояния отдельных групп
населения.
Для изменения неравенства в доходах используется кривая М.
Лоренца, отражающая неравномерность распределения какого-либо
признака, а в данном случае показывающая, какую часть совокупного
денежного дохода страны получает каждая доля низкодоходных и
высокодоходных семей, то есть отражает в процентах распределение
дохода между семьями с разным достатком (рисунок 1) [1].
Кривая Лоренца наглядно показывает, насколько фактическое
распределение
доходов между разными
семьями отличается
равномерного распределения.
Кривая Лоренца
Е
% 100
дохода80
D
Линия
РР
60
40
С
Кривая Л
20
А
0
0
В
50
F
% семей
Рисунок 1 – Кривая Лоренца
100
от
Если имеет место равенство доходов, то оно отражается прямой
линией ОЕ. Ломаная линия ОFЕ – это линия абсолютного неравенства.
Если имеет место неравенство в доходах, то линия OABCDE отражает
фактическое распределение доходов и называется кривой Лоренца. Чем
больше отклоняется эта линия от линии ОЕ, тем больше неравенство в
распределении
концентрации
доходов.
доходов,
Кроме
того,
измеряющий
используется
насколько
индекс
фактическое
распределение доходов по численно равным группам населения
отличается от их равномерного распределения. Если
разделить
площадь OABCDE на площадь треугольника OFE, то получим
показатель,
доходов,
отражающий
и
чем
больше
степень
это
неравенства
отношение,
в
тем
распределении
несправедливее
распределение. Такой показатель называется коэффициентом Джини.
Коэффициент Джини [6] позволяет сравнивать распределение
признака в совокупностях с различным числом единиц (например,
регионы с разной численностью населения); дополняет данные о ВВП и
среднедушевом доходе и может быть использован для сравнения
распределения признака (дохода) между различными совокупностями,
а также может быть использован для сравнения распределения
признака
(дохода)
отслеживать
по
динамику
разным
группам
неравномерности
населения
и
распределения
позволяет
признака
(дохода) в совокупности на разных этапах.
Рассмотрим динамику коэффициента Джини в России [6].
Коэффициент Джини в России в 1991 г. составлял 26%, в 1992 г. –
28,9%, в 1994 г. – 40,9%, в 1998 г. – 37,9%. По данным Росстата,
коэффициент Джини в России в течение 10 последних лет практически
не
меняется,
колеблясь
вокруг
значения
0,4.
По
степени
дифференциации доходов Россия примыкает к группе развивающихся
государств, о чем свидетельствует значение коэффициента. Например,
в 2008 году значение коэффициента Джини в США составляет 0,408, в
Великобритании – 0,361, в Швеции – 0,250, в Японии – 0,249, в
Зимбабве – 0,568, в Мексике – 0,537, в Чили – 0,565.
По некоторым оценкам, одна шестая часть населения России
сосредоточила в своих руках 57% всех денежных доходов и 92%
доходов от собственности. Сложившаяся сегодня в России модель
социальной
стратификации
характеризует
в
высшей
степени
дифференцированное общество.
Построение кривой Лоренца и вычисление коэффициента Джини
с помощью MS Excel служит для наглядной демонстрации важных
экономических
закономерностей,
взаимосвязей
и
положений.
Рассмотрим в качестве примера задачу о неравномерности доходов [4].
Таблица 1 – Исходные данные
Группы населения
по уровню
дохода, в тыс.руб
0
Менее 2
От 2 до 3
От 3 до 4
От 4 до 6
От 6 до 8
От 8 до 10
От 10 до 15
От 15 до 20
От 20 до 25
Более 25
Всего
В
таблице
1
Доля населения
в % к итогу
Доля доходов в
% к итогу,
1997г
Доля доходов в
% к итогу,
1998г
Нс
0
10
10
10
10
10
10
10
10
10
10
100
Д97
0
4,3
6,1
7,1
8,1
9,1
10,1
11,2
12,6
14,3
17,1
100
Д98
0
3,2
4,8
6,1
7,2
8,4
9,7
11,3
13,2
15,8
20,3
100
столбец
Нс
содержит
доли
городов
с
соответствующей численностью населения в общем числе городов, а
столбцы Д97 и Д98 – доли доходов каждой группы в совокупных
доходах населения региона соответственно в 1997 году и в 1998. Нули
в первой строке добавлены к реальным данным для того, чтобы все
рассматриваемые далее кривые начинались в начале координат.
Население по уровню дохода разбито на десять групп, так что каждая
группа
составляет
ранжированы
в
по
10%
порядке
всего
населения.
возрастания
Причем
суммарных
группы
доходов,
приходящихся на каждую группу.
2. В столбцах НсК и Д97К, Д98К (таблица 2) подсчитаны
нарастающим итогом суммы частот, заданные в Нс и Д97К, Д98К.
Таблица 2 – Подсчеты суммы частот
Группы
населения по
уровню
дохода, в
тыс.руб
0
Менее 2
От 2 до 3
От 3 до 4
От 4 до 6
От 6 до 8
От 8 до 10
От 10 до 15
От 15 до 20
От 20 до 25
Более 25
Всего
Сделано
Доля
населе
ния в
%к
итогу
Доля
доходов
в%к
итогу,
1997г
Доля
доходов
в%к
итогу,
1998г
Нс
0
10
10
10
10
10
10
10
10
10
10
100
Д97
0
4,3
6,1
7,1
8,1
9,1
10,1
11,2
12,6
14,3
17,1
100
Д98
0
3,2
4,8
6,1
7,2
8,4
9,7
11,3
13,2
15,8
20,3
100
это
соответственно
НсК[i+1]=НсK[i]+Нс[i];
Д97К[1]=0;
Кумуляты
Доля
населения
в%
Доля
доходов
в %, 97г.
Доля
доходов
в %,
98г.
НсК
0
10
20
30
40
50
60
70
80
90
100
Д97К
0
4,3
10,4
17,5
25,6
34,7
44,8
56,0
68,6
82,9
100
Д98К
0
3,2
8,0
14,1
21,3
29,7
39,4
50,7
63,9
79,7
100
по
формулам:
НсК[1]=0;
Д97К[i+1]=Д97К[i]+Д97[i];
Д98К[1]=0; Д98К[i+1]=Д98К[i]+Д98[i].
3.
Для
визуальной
оценки
степени
неравномерности
распределения доходов Д97, Д98 относительно единиц исследуемой
совокупности Нс используется кривая Лоренца (рисунок 2). Кривые
Лоренца для каждого года строятся на одной диаграмме типа Точечная.
Кривые представляют собой графики зависимости кумуляты НсК
от кумуляты Д97К, Д98К. Для построения такой кривой на диаграмме в
качестве абсцисс Х и ординат Y ряда используются соответственно
значения НсК и Д97К, Д98К. Одновременно на диаграмме выводится
диагональ первого квадранта РР, линия равномерного распределения.
Для вывода диагонали первого квадранта необходимо скопировать на
диаграмму диапазон ячеек столбца НсК, а в появившемся окне
поставить галочки «новые элементы рядов» и «в строках».
Рисунок 2 – Кривые Лоренца на диаграмме типа Точечная
4. В качестве показателя концентрации доходов для каждого года
рассчитывается
коэффициент
Джини
(таблица
3).
Для
этого
используется формула:
G=
∑ ÍñÊ
i
i
⋅ Ä 97 Ê i +1 ( Ä 98Ê i +1 ) − ∑ ÍñÊ
i
10000
i +1
⋅ Ä 97 Ê i ( Ä 98Ê i )
.
Таблица 3 – Подсчеты коэффициентов Джини
Группы
населения
по уровню
дохода, в
тыс.руб
Доля
населения
в%к
итогу
Доля
доходов
в%к
итогу,
1997г
Доля
доходов
в%к
итогу,
1998г
Д97
0
4,3
6,1
7,1
8,1
9,1
10,1
11,2
12,6
14,3
17,1
100
0,2104
G=21%
Д98
0
3,2
4,8
6,1
7,2
8,4
9,7
11,3
13,2
15,8
20,3
100
0,28
G=28 %
Нс
0
10
10
10
10
10
10
10
10
10
10
100
0
Менее 2
От 2 до 3
От 3 до 4
От 4 до 6
От 6 до 8
От 8 до 10
От 10 до 15
От 15 до 20
От 20 до 25
Более 25
Всего
G
Кумуляты
Доля
населения
в%
Доля
доходов
в %, 97г.
Доля
доходов
в %,
98г.
НсК
0
10
20
30
40
50
60
70
80
90
100
Д97К
0
4,3
10,4
17,5
25,6
34,7
44,8
56,0
68,6
82,9
100
Д98К
0
3,2
8,0
14,1
21,3
29,7
39,4
50,7
63,9
79,7
100
В итоге получилось, что коэффициент Джини в 1997 году
составил 21%, а в 1998 – 28%. Данные цифры говорят о том, что в 1997
году распределение доходов в обществе было более справедливым, чем
в 1998, а потому и кривая Лоренца, соответствующая 1997 году более
приближена к линии равномерного распределения.
Экономическая модель, рассмотренная в этой работе, ни в коей
мере не претендует на полноту изложения затронутых экономических
проблем,
в
данном
случае
проблемы
бедных
и
богатых
и
неравномерного распределения доходов в обществе. Более того,
следует сразу подчеркнуть, что модель представляет собой всего лишь
небольшой
фрагмент
целых
направлений
экономической
науки.
Указанные кривая и коэффициент используются для характеристики
распределения не только доходов, хотя это самый распространенный
момент, но и какого-либо показателя, в общем.
Переложение математической или экономической задачи на язык
MS Excel позволяет автоматизировать расчеты, получать наглядные
результаты в виде диаграмм. Несомненно, MS Excel сегодня – очень
мощная
развитая
вычислительная
среда,
которая
в
состоянии
обеспечить профессионала всем необходимым для «автономного
плавания» в этой самой среде.
Литература
1.
Гальперин
В.М.,
Игнатьев
С.М.,
Моргунов
В.И.
Микроэкономика – СПб.: Экономическая школа, 2000.
2.
Бондаренко
состоятельных
Н.В.
Особенности
семей//Вестник
адаптации
общественного
бедных
мнения:
и
Данные.
Анализ. Дискуссии, № 1 (81), 2006.
3. Кондрашова С.С. Информационные технологии в управлении:
Учебное пособие – К.: МАУП, 2004.
4. Левит Б.Ю. Диаграммы Excel в экономических моделях – М.:
ФиС, 2004.
5. Лавренов С.М. Excel: Сборник примеров и задач – М.: ФиС,
2005.
6. http://ru.wikipedia.org/wiki/