ЛЕКЦИЯ 11 Критическая точка. Свойства вещества в

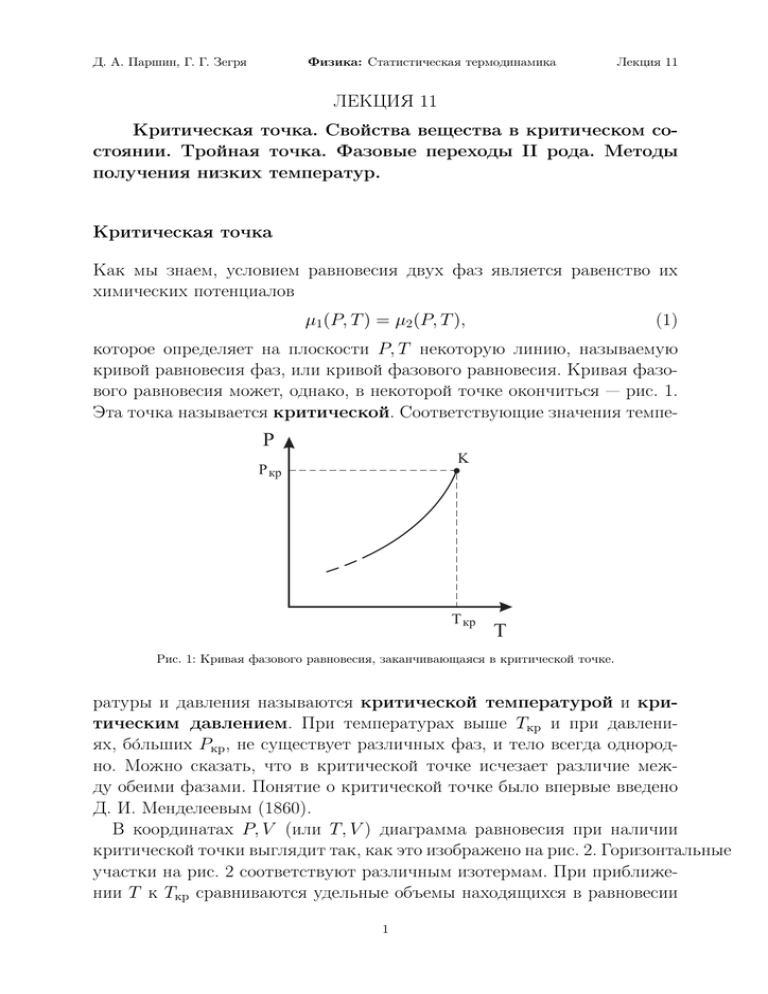
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
ЛЕКЦИЯ 11
Критическая точка. Свойства вещества в критическом состоянии. Тройная точка. Фазовые переходы II рода. Методы
получения низких температур.
Критическая точка
Как мы знаем, условием равновесия двух фаз является равенство их
химических потенциалов
µ1 (P, T ) = µ2 (P, T ),
(1)
которое определяет на плоскости P, T некоторую линию, называемую
кривой равновесия фаз, или кривой фазового равновесия. Кривая фазового равновесия может, однако, в некоторой точке окончиться — рис. 1.
Эта точка называется критической. Соответствующие значения темпе-
P
K
P кр
T кр
T
Рис. 1: Кривая фазового равновесия, заканчивающаяся в критической точке.
ратуры и давления называются критической температурой и критическим давлением. При температурах выше Tкр и при давлениях, бо́льших Pкр , не существует различных фаз, и тело всегда однородно. Можно сказать, что в критической точке исчезает различие между обеими фазами. Понятие о критической точке было впервые введено
Д. И. Менделеевым (1860).
В координатах P, V (или T, V ) диаграмма равновесия при наличии
критической точки выглядит так, как это изображено на рис. 2. Горизонтальные
участки на рис. 2 соответствуют различным изотермам. При приближении T к Tкр сравниваются удельные объемы находящихся в равновесии
1
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
P
K
P кр
Vкр
V
Рис. 2: Кривая равновесия в координатах P, V .
фаз. Например, если речь идет о равновесии жидкость — газ, плотность
газа в критической точке становится равной плотности жидкости. Поскольку и в газе и в жидкости молекулы (или атомы) расположены в
пространстве нерегулярно, беспорядочно, то это значит, что нет и различия между этими двумя фазами.
Поэтому, при наличии критической точки между всякими двумя состояниями вещества может быть произведен непрерывный переход, при
котором ни в какой момент не происходит расслоения на две фазы — для
этого надо менять состояние вдоль какой-либо кривой, огибающей критическую точку и нигде не пересекающей кривую равновесия — рис. 3.
В этом смысле при наличии критической точки становится условным са-
P
K
2
1
T
Рис. 3: Кривая, огибающая критическую точку.
мо понятие о различных фазах, и невозможно во всех случаях указать,
2
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
какие состояния являются одной фазой, а какие — другой. Строго говоря, можно говорить о двух фазах лишь тогда, когда они существуют обе
одновременно, соприкасаясь друг с другом, т. е. в точках, лежащих на
кривой равновесия. Тогда их можно различить, например, визуально, по
различию в оптических свойствах.
Ясно, что критическая точка может существовать лишь для таких
фаз, различие между которыми имеет лишь чисто количественный характер. Таковы, например, жидкость и газ, отличающиеся друг от друга
лишь большей или меньшей плотностью и, соответственно, большей или
меньшей ролью взаимодействия между молекулами.
Если же речь идет о таких фазах, как жидкость и твердое тело (кристалл), или твердое тело и газ, или различных кристаллических модификациях вещества, то здесь, помимо различия в плотности, имеется еще
различие во внутренней симметрии расположения атомов или молекул.
В кристалле атомы расположены в узлах правильной кристаллической
решетки — рис. 4а, а в жидкости или в газе они беспорядочно двигаются по занимаемому ими объему — рис. 4а,б, и никакой симметрии в их
расположении нет. Ясно, что о всяком свойстве (элементе) симметрии
а)
б)
с)
Рис. 4: Расположение атомов: а) в кристалле, б) в жидкости, с) в газе.
можно сказать только либо, что оно есть, либо, что его нет; оно может
появиться или исчезнуть лишь сразу, скачком, а не постепенно. В каждом состоянии тело будет обладать либо одной, либо другой симметрией,
и потому всегда можно указать, к которой из двух фаз оно относится.
Для таких фаз, различающихся своей симметрией, критическая точка
существовать не может и кривая равновесия фаз должна либо уходить
на бесконечность, либо заканчиваться, пересекаясь с кривыми равновесия других фаз.
Наблюдать переход через критическую точку можно следующим об3
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
разом. Для этого берут кварцевую ампулу, частично заполненную жидкостью. Воздух из ампулы удаляют кипячением, после чего ампулу запаивают. В ампуле тогда находится в равновесии жидкость и ее насыщенный пар. Граница между ними (мениск) хорошо видна в силу различия в показателях преломления обеих фаз. Для демонстрации можно
использовать жидкую углекислоту (Tкр = 31◦ С, Pкр = 73 атм) или эфир
(Tкр = 194◦ C, Pкр = 35 атм). Затем ампула равномерно нагревается в
печи. При приближении к критической температуре кривизна мениска
непрерывно уменьшается, поскольку уменьшается поверхностное натяжение на границе жидкость — насыщенный пар. Когда температура достигает Tкр , мениск становится плоским и исчезает совсем. Вещество становится однородным по всему объему ампулы и продолжает оставаться
таковым при дальнейшем нагревании .
Свойства вещества в критическом состоянии
Из условия, что в критической точке производная (∂P/∂V )T обращается
в ноль, следует, что сжимаемость вещества в критической точке обращается в бесконечность:
Ã
!
1 ∂V
γ=
= ∞.
(2)
V ∂P T =Tкр
Это приводит к тому, что при приближении к критической точке, сильно
возрастают флуктуации плотности вещества. Следствием этого является то, что прозрачное в нормальных условиях вещество в критической
точке становится непрозрачным, оно как бы "чернеет". Это происходит
вследствие сильного рассеяния света на флуктуациях плотности с масштабами — порядка длины волны света, а само явление называется критической опалесценцией.
В критической точке обращается в ноль теплота испарения
q ∼ (Tкр − T )β ,
(3)
а теплоемкость обращается в бесконечность
Cv ∼
1
.
|Tкр − T |α
(4)
Показатели степеней в этих и им подобных формулах называются критическими индексами. Их численные значения универсальны, т. е.
4
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
не зависят от конкретного вещества. Они чувствительны лишь к характеру симметрии задачи, числу независимых параметров, которые отличают одну фазу от другой и т. д. Их нахождение является весьма трудной
теоретической проблемой, требующей использования методов так называемой ренормализационной группы и диаграмной техники.
Еще одной интересной особенностью вещества в критическом состоянии является медленность установления равновесного состояния.
Например равновесное распределение плотности (при сохранении температуры строго постоянной) может устанавливаться в течении суток и
дольше.
Тройная точка
Аналогично условиям равновесия двух фаз, равновесие трех фаз одного
и того же вещества определяется равенствами
P1 = P2 = P3 ,
T 1 = T2 = T3 ,
µ 1 = µ2 = µ3 .
(5)
Примером может служить вода (H2 O), тогда речь идет о твердой, жидкой и газообразной фазах. Пусть T и P — общие значения температуры
и давления трех фаз, тогда из равенства их химических потенциалов,
мы получим условия
µ1 (P, T ) = µ2 (P, T ) = µ3 (P, T ).
(6)
Эти условия представляют собой систему двух уравнений с двумя неизвестными P и T :


 µ1 (P, T ) = µ2 (P, T ),
(7)


µ1 (P, T ) = µ3 (P, T ).
Решение этой системы уравнений дает нам пары значений P и T (одну
или несколько) при которых три фазы могут находиться в равновесии
друг с другом. Каждая такая пара определяет точку на плоскости P ,
T — так называемая тройная точка. На диаграмме P , T тройная точка (точка A) изображается как точка пересечения кривых равновесия
каждых двух из трех фаз (рис. 5; области I, II, III — области трех однородных фаз — газообразной, жидкой и твердой, соответственно). Кривая
равновесия между газом (I) и жидкостью (II) называется кривой испарения. Эта кривая начинается в тройной точке, а заканчивается, как
этого и следовало ожидать, в критической точке K. Кривая равновесия
твердой (III) и жидкой (II) фаз называется кривой плавления. Она
5
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
P
Лекция 11
K
II
жидк
III
тв.тело
Pтр
A
T тр
I
газ
T
Рис. 5: Тройная точка A равновесия трех фаз: газ (I), жидкость (II) и твердое тело (III). См. рис.
136 на стр. 462 Сивухина.
также начинается в тройной точке и поскольку эти фазы различаются
по симметрии, кривая плавления уходит в бесконечность. Она, как мы
уже говорили, не может закончиться в критической точке, поскольку
таковой для равновесия твердое тело — жидкость не существует 1 . И,
наконец, кривая равновесия твердой (III) и газообразной (I) фаз называется кривой возгонки. Все эти три кривые равновесия пересекаются
в тройной точке A.
В силу уравнения Клапейрона — Клаузиуса
dP
q
=
dT
T (v2 − v3 )
(8)
вдоль кривой равновесия твердое тело — жидкость. Для воды v2 < v3
и dP/dT < 0, как показано на рис. 5. У других веществ при плавлении
объем увеличивается и тогда dP/dT > 0.
Очевидно, что
равновесие более чем трех фаз одного и того же вещества
невозможно.
Для воды тройная точка лежит на 0.008◦ выше точки плавления при
нормальном атмосферном давлении. Давление же в тройной точке намного меньше атмосферного и равно примерно 4.58 мм рт. ст. — рис. 6 2 .
Тройная точка для всякого вещества является вполне определенной веА что будет в случае равновесия аморфного твердого тела — жидкость? Ведь аморфное тело, в
отличие от кристаллического, никакой симметрией не обладает.
2 Как видно из параметров тройной точки воды, при нормальных условиях равновесное сосуществование льда, водяного пара и жидкой воды невозможно. Это обстоятельство вроде бы противоречит обыденным наблюдениям — лёд, вода и пар часто наблюдаются одновременно. Но противо1
6
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
Рис. 6: Тройная точка воды. Обозначены температура кристаллизации (плавления) — Tкр и температура кипения — Tкип при нормальном атмосферном давлении
личиной (в отличие, например, от температуры кипения, которая зависит от давления). С этим связано то обстоятельство, что тройная точка воды является основной реперной точкой при построении абсолютной
термодинамической шкалы температур Кельвина, а также практической
международной шкалы температур Цельсия.
Кривые испарения, плавления и возгонки, показанные на рис. 5, делят
плоскость P, T на три области I, II, III. Точкам области I соответствует газообразное, области II — жидкое, области III — твердое состояние
вещества. Плоскость P, T с указанными тремя кривыми равновесия называется диаграммой состояния. Диаграмма состояния позволяет судить, какие будут происходить фазовые превращения при том или ином
процессе.
Допустим, например, что производится нагревание при постоянном
давлении. На диаграмме состояния такой процесс представляется горизонтальной прямой — рис 7. Если эта прямая проходит выше тройной, но
ниже критической точки, то в точке B она пересечет кривую плавления,
а в точке C — кривую испарения. Значит, при нагревании твердое тело
сначала расплавится (точка B), а затем жидкость испарится (точка C).
Для многих веществ давление, соответствующее тройной точке, меньше 1 атм. Такие вещества при нагревании при атмосферном давлении
плавятся. Если же указанная прямая проходит ниже тройной точки, то
она пересечет только кривую возгонки в некоторой точке D, в которой и
речия нет — наблюдаемые состояния далеки от термодинамически равновесных и реализуются на
практике только из-за кинетических ограничений фазовых переходов.
7
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
P
Лекция 11
K
III
II
тв.тело
жидк
C
B
A
I
газ
D
T
Рис. 7: Фазовые превращения. Рис. 136, стр. 462 Сивухина.
произойдет непосредственное превращение твердого тела в газообразное
состояние. Промежуточного состояния не будет! Такое явление еще называется сублимацией. Оно хорошо наблюдается для твердой углекислоты (CO2 ). Это объясняется тем, что давление в тройной точке углекислоты выше атмосферного давления: Tтр = −56.6◦ C, Pтр = 4.8 атм. При
атмосферном давлении углекислота не может находится в жидком
состоянии. Поэтому при нагревании на воздухе твердая углекислота испаряется! Помните сухой лед у мороженщиц? Он испаряется (дымится),
но не плавится! По тем же причинам обычный лед также превращается
в пар — мокрое белье высыхает на морозе (???).
а)
б)
a
a
a = 90
a =/ 90
Рис. 8: Две кристаллических модификации серы — а) моноклинная, б) ромбическая.
Тройных точек может быть несколько, если число фаз, в которых
8
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
может находиться химически однородное вещество при всевозможных
значениях температуры и давления превышает три. Например сера в
твердом состоянии может существовать в двух кристаллических модификациях — моноклинной и ромбической — рис. 8. Элементарная ячейка
в моноклинной модификации серы представляет собой прямой параллелепипед с основанием в виде параллелограмма (α 6= 90◦ ). В отличие от
нее, элементарная ячейка ромбической системы обладает бо́льшей симметрий. Она представляет собой прямоугольный параллелепипед с прямоугольным основанием (α = 90◦ ).
Поскольку эти две кристаллические модификации серы отличаются по
симметрии, на диаграмме состояния серы имеются три тройные точки,
а именно S, T , L, — рис. 9. Область моноклинной модификации огра-
P
F
K
N
M
L
ромб
M
жидк
N2
N1
мон
G
R
Q
P
T
газ
S
T
Рис. 9: Диаграмма состояния серы. Стр. 464 Сивухина.
ничена треугольником ST L. Область ромбической модификации лежит
выше кривой GSLF . Возьмем ромбические кристаллы серы при комнатной температуре и нормальном давлении и будем нагревать их, сохраняя давление постоянным. Этот процесс изобразится горизонтальной
прямой M N1 N2 Q. В точке N1 , где эта прямая пересекает кривую равновесия между двумя кристаллическими модификациями, ромбические
кристаллы превращаются в моноклинные (при атмосферном давлении
точке N1 соответствует температура 95.5◦ C). В точке N2 (при температуре 119.2◦ C) моноклинные кристаллы плавятся. В точке P (при температуре 444.6◦ C) жидкая сера закипает. При охлаждении вещества те
же превращения будут происходить в обратном порядке. Если ромбические кристаллы взять в состоянии M 0 под давлением выше давления в
9
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
тройной точке L (1280 атм), то изобара M 0 R0 пройдет выше этой точки.
Поэтому превращения ромбических кристаллов в моноклинные происходить не будет. Ромбические кристаллы в точке N 0 будут сразу плавиться.
Фазовые переходы второго рода
До сих пор, при обсуждении фазовых превращений мы говорили, что в
точке фазового перехода скачкообразно меняются такие величины как
удельная энтропия, удельный объем. С изменением удельной энтропии
связано также выделение или поглощение тепла при переходе. В точке
перехода состояние обеих фаз различно. Такие фазовые переходы называют фазовыми переходами I рода.
Однако бывают ситуации, когда в точке перехода никакого различия
между обеими фазами нет. Соответственно не испытывают скачка удельная энтропия, удельный объем и другие характеристики, связанные с
первыми производными функции µ(P, T ). Такие фазовые переходы называются фазовыми переходами II рода. При них не происходит
скрытого выделения или поглощения тепла. То есть первые производные от термодинамических потенциалов, как например
Ã
!
Ã
!
∂µ
∂µ
s=−
и
v=
,
(9)
∂T P
∂P T
не испытывают скачка в точке перехода.
Зато при фазовых переходах II рода имеют особенности вторые производные от термодинамических функций. Например, теплоемкость в
точке перехода обращается в бесконечность
Ã
∂S
Cp = T
∂T
!
.
(10)
P
Пример фазового перехода II рода — рис. 10. При изменении температуры, равновесная позиция атома B смещается к центру элементарной
ячейки. В точке T = Tc скачком меняется только симметрия решетки.
Однако как плотность, так и энтропия оказываются непрерывными в
точке перехода.
К фазовым переходам II рода относится переход из ферромагнитного состояния в парамагнитное. При некоторой температуре, называемой точкой Кюри пропадает дальний магнитный порядок, существовавший в веществе при T < Tc . Электрическим аналогом такого
перехода является сегнетоэлектрический фазовый переход. Фазовым
10
Д. А. Паршин, Г. Г. Зегря
A
Физика: Статистическая термодинамика
Лекция 11
B
T < Tc
T > Tc
Рис. 10: Пример фазового перехода II рода.
переходом II рода является также переход нормального металла в сверхпроводящее состояние.
Фазовые переходы II рода возможны также и в жидкостях. Примером
является переход жидкого гелия в состояние сверхтекучести, открытое
П. Л. Капицей в 1938 г. (Нобелевская премия по физике за 1978 г.). Вязкость такой жидкости ниже температуры фазового перехода оказывается
точно равной нулю. Теория сверхтекучего гелия-II была разработана Л.
Д. Ландау (Нобелевская премия по физике за 1962 год).
Свойства вещества в точке фазового перехода II рода напоминают
свойства в критической точке при фазовых переходах I рода. Здесь тоже
есть универсальность, важную роль играют флуктуации и т. д. Схематически разницу между фазовыми переходами I и II рода можно изобразить следующим образом — рис. 11 и рис. 12.
F
F
F
II
I
II
I
I
T < Tc
v
T = Tc
II
v
Рис. 11: Фазовый переход I рода.
11
T > Tc
v
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
F
F
F
Лекция 11
I
I
I
T > Tc
X
II
II
X
T = Tc
T < Tc
X
Рис. 12: Фазовый переход II рода.
Методы получения низких температур
В технике применяются три основных метода для получения низких температур 3 :
1. Испарение жидкостей. На этом принципе работают домашние холодильники.
2. Использование эффекта Джоуля — Томсона. Охлаждение основано исключительно на отклонении газа от идеальности.
3. Обратимое адиабатическое расширение газа с совершением
внешней работы. При этом охлаждаться может даже идеальный
газ.
4. Охлаждающие смеси. Так, путем смешения поваренной соли со
снегом можно получить температуру ниже -20◦ С, а смешением хлороформа или эфира с твердой углекислотой дает температуру -77◦ С.
Остановимся подробнее на методе 3. При обратимом адиабатическом
расширении газа остается постоянной его энтропия S:
Ã
∂S
∆S =
∂T
!
Ã
∂S
∆T +
∂P
P
!
∆P = 0.
(11)
T
Поскольку, по определению, Cp = T (∂S/∂T )P (см. лекцию 5, формулу
10), то
Ã
!
∂S
Cp
=
.
(12)
∂T P
T
В лекции 8 мы получили формулу (35), основанную на выражении для
дифференциала термодинамического потенциала dΦ = −SdT + V dP и
3
см. стр. 408 Д. В. Сивухина "Термодинамика и молекулярная физика".
12
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
равенстве смешанных производных:
Ã
∂S
∂P
!
T
Ã
∂V
=−
∂T
!
.
(13)
P
Используя эти соотношения, мы получаем из уравнений (11), (12) и (13)
Ã
∆T
T ∂S
=−
∆P
Cp ∂P
Ã
!
T
T ∂V
=
Cp ∂T
!
.
(14)
P
Для идеального газа V = N T /P и (∂V /∂T )P = N/P . В результате
∆T /∆P = V /Cp > 0. Поэтому ∆T < 0, если ∆P < 0, т. е. газ расширяется. Причина охлаждения очевидна. Молекулы газа отражаются
от движущегося от них поршня с меньшими скоростями, чем налетают на него. В результате газ совершает работу, и кинетическая энергия,
а значит и температура газа, уменьшается. Формула (14) описывает так
называемый дифференциальный эффект, когда изменения температуры газа и давления невелики. Однако мы без труда можем рассмотреть
и интегральный эффект, когда изменения этих величин не являются
малыми. Ограничимся для этого случаем одноатомного идеального газа.
В лекции 7 мы получили формулу (33) для энтропии одноатомного
идеального газа
eV
S = N ln
− N f 0 (T ),
(15)
N
где функция f (T ) определялась формулой (28)

Ã
f (T ) = −T ln T 3/2
m
2πh̄2
!3/2 
.
(16)
Из этих двух формул следует, что изменение энтропии газа при его переходе из состояния T1 , V1 в состояние T2 , V2 равно
Ã
!
Ã
!
3
T2
V2
+ N ln
.
∆S = S2 − S1 = N ln
V1
2
T1
(17)
Приравнивая ∆S нулю, получаем
Ã
T2 = T1
V1
V2
!2/3
,
или
T V 2/3 = const.
(18)
При расширении V2 > V1 , и тогда из этой формулы следует, что T2 < T1 ,
т. е. имеет место охлаждение газа. Заметим только, что пользоваться
этой формулой оправданно лишь пока газ можно считать идеальным.
При низких температурах, в особенности вблизи температуры сжижения
13
Д. А. Паршин, Г. Г. Зегря
Физика: Статистическая термодинамика
Лекция 11
газа, она несправедлива и необходимо вернуться к дифференциальному
соотношению (14). Из него получаем интегральный эффект
ZP2
T2 − T 1 =
P1
Ã
T ∂V
Cp ∂T
!
dP.
(19)
P
Если коэффициент теплового расширения (∂V /∂T )P положителен (как у
газов), то при адиабатическом расширении получается охлаждение. Достоинством этой формулы является то, что при ее выводе не требовалось
предположений об идеальности газа.
14