Государственное бюджетное образовательное учреждение дополнительного образования детей 350000 г. Краснодар,
реклама

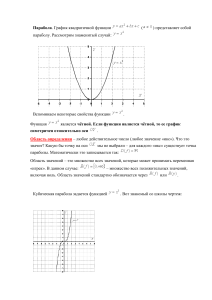
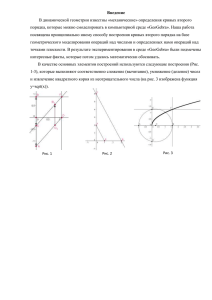
Государственное бюджетное образовательное учреждение дополнительного образования детей «Центр дополнительного образования для детей» 350000 г. Краснодар, ул. Красная,76 тел. 259-84-01 E-mail:cdodd@mail.ru КРАЕВЫЕ ЗАОЧНЫЕ КУРСЫ «ЮНИОР» Математика 8 класс ответы и решения к работе № 2, 2012-2013 уч. год Задание 1. После урока на доске остался график функции y=к/х и пять прямых, параллельных прямой y=kx, (k≠0). Найдите произведение абсцисс всех десяти точек пересечения. Решение Любая прямая, параллельная прямой y=kx , имеет уравнение y=kx+b , где b – некоторая константа. Абсциссами точек её пересечения с гиперболой y= к/х являются оба корня уравнения к/х =kx+b . Оно равносильно квадратному уравнению kx 2+bx-k=0 . По теореме Виета произведение корней этого уравнения равно =-1 . Перемножив пять таких произведений, получаем ответ. Комментарии. 1. Каждое из указанных квадратных уравнений имеет два действительных корня, поскольку имеет дискриминант b2+4k2>0 . Геометрически это как раз означает, что любая прямая, параллельная прямой y=kx , пересекает гиперболу y= к/х в двух точках. Так же, как в решении, можно доказать более общий факт – произведение абсцисс точек пересечения прямой и гиперболы y= к/х зависит только от k и угла наклона прямой. Ответ: -1 . Задание 2. Доказать, что выражение + =2, если 1≤a ≤2 , и равно 2 , если a>2 Решение │ + -1│= = + =│ +1│+ Задание 3. На координатной плоскости xOy построена парабола y = x2. Затем начало координат и оси стёрли. Как их восстановить с помощью циркуля и линейки (используя имеющуюся параболу)? Решение Докажем следующую лемму: Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы (рис. 1). рис. 1 Доказательство. Пусть хорды AB и CD параболы лежат на параллельных прямых y = kx + a и y = kx + b, тогда абсциссы точек A, B, C, D – это корни уравнений x2 = kx + a и x2 = kx + b, а абсциссы точек M и N – полусуммы корней этих уравнений, то есть по теореме Виета равны k/2. Следовательно, прямая MN параллельна оси Oy. Вернёмся к решению задачи. Проводим последовательно две параллельные хорды параболы; прямую, проходящую через их середины (параллельную Oy); перпендикуляр к этой прямой, пересекающий параболу в двух точках; серединный перпендикуляр к полученной хорде. Этот перпендикуляр и будет осью Oy, а ось Ox – это перпендикуляр к Oy в точке пересечения с параболой. Задание 4. Сравните без помощи калькулятора числа: Решение Рассмотрим разность между данными числами: = = ,так как первая дробь больше второй. Действительно, числитель первой дроби больше числителя второй, а знаменатель — меньше, так как первая дробь больше второй. Действительно, числитель первой дроби больше числителя второй, а знаменатель — меньше. Задание 5. x 1 2 Решить уравнение: 1 2x x 2 x3 x3 5. Указание: воспользоваться известным свойством a 2 a . Ответ:x=2; x= -2. Задание 6. Не вычисляя корней x1 ; x 2 ; многочлена f x ax 2 bx c , где a 0 , дать метод нахождения значения выражения Sn x1n x2n для любого натурального n через коэффициенты a, b, c . Решение. По формулам Виета x1 x 2 2 c c b S 2 x x x1 x 2 2 x1 x2 2 x1 x 2 . , где a a a n n n 1 n 1 n 1 n 1 Рассмотрим S n x1 x2 x1 x2 x1 x2 x1 x2 x2 x1 2 1 2 2 b S1 . a 2 S n 1 x1 x 2 x1 x 2 x 2n 2 x1n 2 S n 1 x1 S2 Найдем b 2 2c b 2 2ac . a2 a a2 x 2 S n 2 x1 x 2 Итак, b c S n 1 S n2 a a b c S n S n 1 S n 2 . Из полученного тождества можно определять выражения для a a S 3 , S 4 ,... через коэффициенты a, b, c . Далее отметим следующее. Если рассмотреть выражения ax 2 bx c и выделить в нем полный квадрат, то получим 2 2 b b 2 4ac b D 2 ax bx c a x a x . Откуда видно, что выражение 2a 4a 2a 4a b если a 0 ; наибольшее ax 2 bx c принимает наименьшее значение при x 2a b значения также при x если a 0 . Графиком квадратичной функции 2a b 4ac b 2 y f x ax 2 bx c , где a 0 является парабола с вершинами в точке ; . 4a 2a b Ветви параболы направлены вверх при a 0 и вниз при a 0 . Прямая x является 2a осью симметрии параболы y ax 2 bx c . Если D b 2 4ac 0 , то точки пересечения параболы y ax 2 bx c с осью OX есть корни x1, x2 квадратного уравнения y ax 2 bx c = 0 . Если D b 2 4ac 0 , то парабола касается оси OX в точке x b . 2a Если D 0 , то пересечений параболы y ax 2 bx c с осью OX нет. Задание 7. Найти все значения параметра a , при которых вершина параболы y f x x 2 ax 5 расположена на координатной плоскости: а) слева от оси OX; б) выше оси OX; в) на оси OX. Решение a a2 a2 a a 2 20 а) координаты вершины параболы y x ax 5 есть ; 5 ; , 2 4 2 4 2 2 поэтому вершина параболы слева от оси OX , если ее абсцисса меньше нуля, т.е. a 0 , откуда a 0 . 2 a 2 20 б) вершина выше оси OX, если ордината больше нуля, т.е. 0 , откуда a 2 20 , 4 т.е. при a 2 5 . a 2 20 в) вершина параболы на оси OX, если ордината равна нулю, т.е. 0, 4 следовательно a 2 20 или a 2 5 , т.е. при a1 2 5 и a 2 2 5 . Далее отметим следующее: для того, чтобы уравнение f x ax 2 bx c 0 имело действительные корни, лежащие на числовой оси левее числа А, является одновременное выполнение следующих неравенств: D b 2 4ac 0; x B f x ax 2 bx c 0 b d и 2a af A 0 . Чтобы уравнение имело действительные корни, больше данного числа А, необходимо и достаточно, чтобы D b 2 4ac 0; b d ; a f A 0 . Наконец, для того 2a , чтобы уравнение f x ax 2 bx c 0 имело один корень меньше A, а другой больше А необходимо и достаточно, чтобы b 2 4ac 0 , a f ( A) 0 .