Одномерные случайные величины

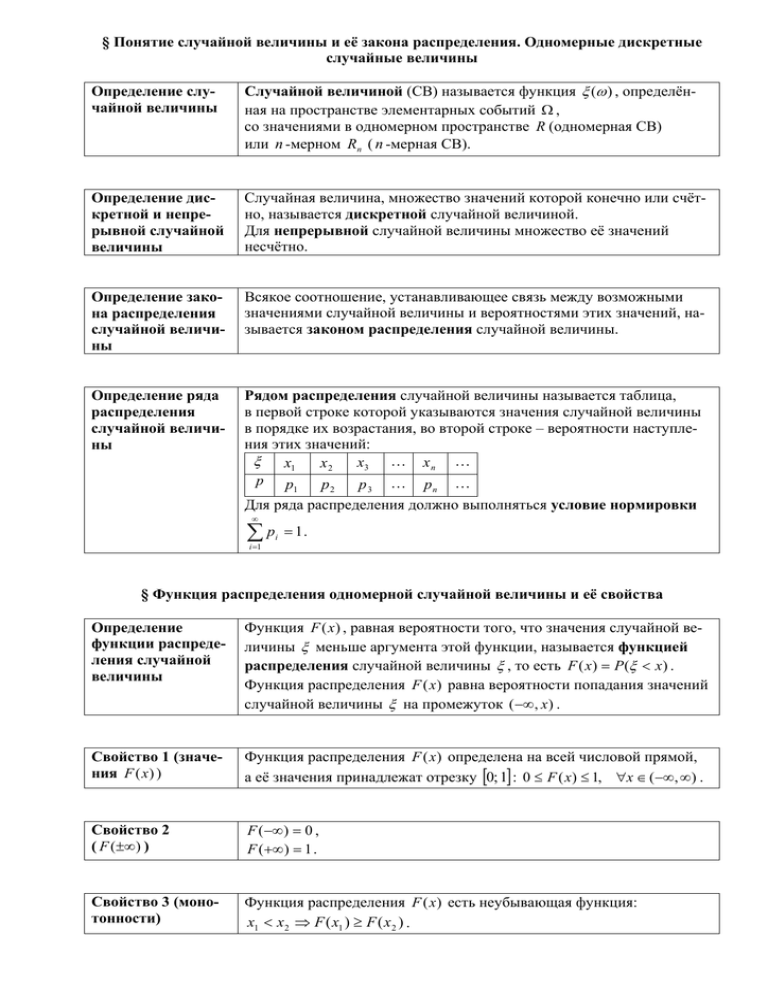
§ Понятие случайной величины и её закона распределения. Одномерные дискретные
случайные величины
Определение случайной величины
Случайной величиной (СВ) называется функция ξ (ω ) , определённая на пространстве элементарных событий Ω ,
со значениями в одномерном пространстве R (одномерная СВ)
или n -мерном Rn ( n -мерная СВ).
Определение дискретной и непрерывной случайной
величины
Случайная величина, множество значений которой конечно или счётно, называется дискретной случайной величиной.
Для непрерывной случайной величины множество её значений
несчётно.
Определение закона распределения
случайной величины
Всякое соотношение, устанавливающее связь между возможными
значениями случайной величины и вероятностями этих значений, называется законом распределения случайной величины.
Определение ряда
распределения
случайной величины
Рядом распределения случайной величины называется таблица,
в первой строке которой указываются значения случайной величины
в порядке их возрастания, во второй строке – вероятности наступления этих значений:
ξ x1
x3 … x n …
x2
p p
p 3 … pn …
p2
1
Для ряда распределения должно выполняться условие нормировки
∞
∑p
i =1
i
= 1.
§ Функция распределения одномерной случайной величины и её свойства
Определение
функции распределения случайной
величины
Функция F (x ) , равная вероятности того, что значения случайной величины ξ меньше аргумента этой функции, называется функцией
распределения случайной величины ξ , то есть F ( x) = P (ξ < x ) .
Функция распределения F (x ) равна вероятности попадания значений
случайной величины ξ на промежуток ( −∞ , x ) .
Свойство 1 (значения F (x ) )
Функция распределения F (x ) определена на всей числовой прямой,
а её значения принадлежат отрезку [0; 1] : 0 ≤ F ( x) ≤ 1, ∀x ∈ ( −∞, ∞ ) .
Свойство 2
( F (±∞ ) )
F (−∞ ) = 0 ,
F ( +∞ ) = 1 .
Свойство 3 (монотонности)
Функция распределения F (x ) есть неубывающая функция:
x1 < x2 ⇒ F ( x1 ) ≥ F ( x 2 ) .
Свойство 4 (непрерывность слева)
Функция распределения F (x ) непрерывна слева в каждой точке x 0 :
∃F ( x0 ) = lim F ( x), ∀x < x0 .
x → x0
x < x0
Свойство 5 (вероятность попадания
в полуинтервал)
Вероятность попадания случайной величины ξ в полуинтервал
[x1 , x2 ) равна разности значений функции распределения F (x) в конечных точках полуинтервала: P( x1 ≤ ξ < x2 ) = F ( x2 ) − F ( x1 ) .
Свойство 6 (правосторонний предел)
Правосторонний предел функция распределения F (x ) в любой точке
x 0 равен вероятности попадания случайной величины ξ на полуинтервал (− ∞, x0 ] : lim F ( x) = P(ξ ≤ x0 ), ∀x > x0 .
x → x0
x > x0
Связь ряда распределения и функции
распределения
Ряд распределения дискретной случайной величины
ξ x1
x3 … x n
x2
p p
… p
p
p
1
2
3
n
связывает с функцией распределения F (x ) равенство
n
F ( x) = ∑ p i ⋅ η ( x − xi ) ,
i =1
⎧0, x ≤ xi ,
где η ( x − xi ) = ⎨
– единичная функция Хевисайда.
⎩ 1, x > xi
Графики функции распределения F (x ) дискретной и непрерывной случайной величины
Дискретные случайные величины ξ :
Непрерывные случайные величины ξ :
Ω→R
Ω→R
Функция распределения F(x)
Функция распределения F(x)
F ( x) = P (ξ < x)
F ( x) = P (ξ < x)
Свойство 7 (скачки
дискретной случайной величины)
Функция распределения F (x ) дискретной случайной величины является ступенчатой со скачками в точках xi разрыва 1-го рода, равными
вероятности p ( xi ) наступления соответствующего значения xi ,
i = 1, 2, ..., n .
§ Плотность распределения одномерной случайной величины и её свойства
Определение непрерывной случайной величины
Случайная величина ξ называется абсолютно непрерывной в точке
x , если её функция распределения F (x ) дифференцируема в этой
точке, то есть ∃F / ( x) .
Определение плотности распределения случайной величины
Плотностью распределения ρ (x ) случайной величины ξ называется
P ( x ≤ ξ < x + Δx )
предел lim
отношения вероятности попадания слуΔx → 0
Δx
чайной величины ξ на полуинтервал [x, x + Δx ) к приращению Δx ,
P ( x ≤ ξ < x + Δx )
F ( x + Δx) − F ( x)
то есть ρ ( x) = lim
, если этот
= lim
Δx → 0
Δ
x
→
0
Δx
Δx
предел существует и конечен.
Свойства функции
распределения
Если случайная величина ξ абсолютно непрерывна, то плотность
распределения ρ (x ) существует и при этом
/
;
1. ρ ( x ) = F ( x )
b
3. P ( a ≤ ξ < b) = ∫ ρ ( x )dx;
2. ρ ( x ) ≥ 0;
a
∞
4. ∫ ρ ( x ) dx = 1;
x
5. F ( x ) =
−∞
∫ ρ ( x)dx.
−∞
§ Математическое ожидание случайной величины и его свойства
Определение математического ожидания ДИСКРЕТНОЙ случайной
величины
Пусть дискретная случайная величина задана рядом распределения
ξ x1
x3 … x n …
x2
p p
… p …
p
p
1
Если ряд
3
2
∞
∑x
k =1
k
n
⋅ p k сходится, то его сумма называется математиче-
ским ожиданием случайной величины ξ . Математическое ожидание
обозначают одним из символов M [ξ ], mξ , < ξ >, ξ . То есть
∞
M [ξ ] = mξ = ∑ x k ⋅ p k .
k =1
Если число значений случайной величины конечно и равно n , ряд заn
меняется конечной суммой M [ξ ] = mξ = ∑ x k ⋅ p k .
k =1
Определение математического ожидания НЕПРЕРЫВНОЙ случайной величины
∞
Если несобственный интеграл
∫ xρ ( x)dx
сходится, то он называется
−∞
математическим ожиданием случайной величины ξ .
∞
Если несобственный интеграл
∫ xρ ( x)dx
−∞
расходится, то случайная
величина ξ математического ожидания не имеет.
Математическое
ожидание функции
случайной величины
1.
Математическое ожидание M [Y ] функции Y = ϕ (ξ ) дискретn
ной случайной величины ξ равно M [Y ] = ∑ ϕ ( x k ) ⋅ p k .
k =1
2.
Математическое ожидание M [Y ] функции Y = ϕ (ξ ) непрерывной случайной величины ξ , заданной на промежутке (a, b ) равно
b
M [Y ] = ∫ ϕ ( x) ρ ( x)dx .
a
Свойства математического ожидания
1. M (C ) = C , C = const;
2. M (Cξ ) = CM (ξ );
3. M (α 1ξ + ... + α nψ ) = α 1 M (ξ ) + ... + α n M (ψ ),
α 1 ,...,α n − const;
4. M (ξ ⋅ψ ) = M (ξ ) ⋅ M (ψ ), ξ ,ψ − независимые.
§ Мода, медиана, квантиль порядка p
Определение моды
случайной величины
Модой mod ξ дискретной случайной величины ξ называется то её
значение, которое достигается с наибольшей вероятностью:
mod ξ = x max P ( xi ) .
Модой mod ξ непрерывной случайной величины ξ называется то её
значение, при котором плотность распределения имеет максимум:
mod ξ = x max ρ ( x ) .
Определение квантили порядка p и
медианы
Квантилью порядка p случайной величины ξ называется точка η p
вещественной оси, в которой функция распределения F (x ) переходит
от значений, меньших p , к значениям, большим p :
F (η p − 0) ≤ p, F (η p + 0) > p .
Квантиль η 1 порядка
2
1
называется медианой случайной величины.
2
p
ηp
§ Дисперсия случайной величины
Определение дисперсии случайно
величины и среднего квадратичное
отклонения
Дисперсией Dξ = D[ξ ] называется математическое ожидание квадрата отклонения этой случайной величины от её математического ожидания:
[
Dξ = D[ξ] = M (ξ −mξ )2
].
Средним квадратичным отклонением называется число σ , равное
квадратному корню из дисперсии: σ = D[ξ ] .
Формулы вычисления дисперсии
Для дискретной случайной величины с рядом распределения
ξ x1
x3 … x n …
x2
p p
… p …
p
p
1
3
2
n
дисперсия вычисляется по формуле: Dξ = D[ξ ] =
∞
∑ (x
k =1
k
− mξ ) 2 p k .
Для непрерывной случайной величины, заданной на промежутке
( a, b) плотностью распределения ρ (x ) , дисперсия равна
b
Dξ = D[ξ ] = ∫ ( x − mξ ) 2 ρ ( x)dx .
a
Если непрерывная случайная величина задана на всей числовой прямой, то её дисперсия вычисляется по формуле:
Dξ = D[ξ ] =
∞
∫ ( x − mξ )
2
ρ ( x)dx .
−∞
Теорема об эквиДисперсия случайной величины ξ равна разности математического
валентной формуле ожидания квадрата случайной величины M ξ 2 и квадрата её матемадля дисперсии
тического ожидания (mξ ) 2 :
[ ]
[ ]
Dξ = D[ξ ] = M ξ 2 − (mξ ) 2 .
Свойства дисперсии
1. D(C ) = 0, C = const;
2. D(α1ξ1 + ... + α nξ n ) = α12 D(ξ1 ) + ... + α n2 D(ξ n ),
α1 ,...,α n − const,
ξi , ξ j − незав. (i, j = 1,2,...n, i ≠ j )
§ Моменты случайной величины
Начальные моменты
[ ]
Начальным моментом k -го порядка называется число m k = M ξ k .
Для дискретной случайной величины m k =
∑x
k
j
p j , j = 1,2,... ;
j
∞
Для непрерывной случайной величины m k =
k
ρ ( x)dx .
−∞
m1 = M [ξ ] .
Центральные моменты
∫x
Центральным моментом k -го порядка называется число
μ k = M (ξ − mξ ) k .
[
]
Для дискретной случайной величины
μ k = ∑ ( x j − M (ξ )) k p j , j = 1,2,...
j
Для непрерывной случайной величины μ k =
∞
∫ ( x − M (ξ ))
−∞
k
ρ ( x) dx .
Свойство центральных моментов
Если случайная величина распределена симметрично относительно
математического ожидания, то все её центральные моменты нечётного порядка равны нулю.
Определение коэффициента асимметрии (скошенности)
Нормальное распределение:
Число A[ξ ] =
μ3
называется коэффициентом асимметрии (скоσ3
шенности). Характеризует степень отклонения распределения
от нормального
ρ ( x) =
1
σ 2π
−
e
( x−a )2
2σ 2
, .для которого
A[ξ ] = 0 .
Если асимметрия положительна, то максимальная ордината
кривой плотности смещена влево на фоне кривой плотности
нормального распределения (график асимметричен влево) и
смещена тем более, чем больше асимметрия.
При отрицательной асимметрии кривая плотности смещена
вправо.
Определение эксцесса
(коэффициента островершинности)
Нормальное распределение:
Число E[ξ ] =
μ4
− 3 называется эксцессом случайной величиσ4
ны, или коэффициентом островершинности. Характеризует степень отличия распределения от нормального
ρ ( x) =
1
σ 2π
−
( x −a )2
e
2σ 2
, для которого E[ξ ] = 0 .
Если E[ξ ] > 0 , ордината максимума плотности распределения
выше ординаты максимума нормального распределения (график остроконечен),
если E[ξ ] < 0 , то – ниже (график тупоконечен).
Связь начальных и
центральных моментов
∀μ 1= 0, μ 2 = D(ξ );
μ 3 = m3 − 3m1m2 + 2m13 ;
μ 4 = m4 − 4m1m3 + 6m2 m12 − 3m14 .
§ Основные дискретные и непрерывные распределения
(см. ОК с. 71, 72)