Электромагнитное излучение в среде. Плотность мод, закон
реклама

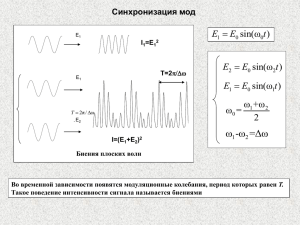
Электромагнитное излучение в среде.
Плотность мод, закон дисперсии
• уравнения Максвелла
• материальные уравнения
• волновое уравнение
• плотность мод электромагнитного поля
• вероятность спонтанного излучения
Уравнения Максвелла. Общий вид
первая пара уравнений Максвелла – векторная:
4π
1 ∂D
=
rot H −
j
c ∂t
c
1 ∂B
=0
rot E +
c ∂t
вторая пара уравнений Максвелла – скалярная:
div D = 4πρ
H, B, D, E
div B = 0
- магнитный вектор, магнитная индукция, электрическое
смещение и электрический вектор
- плотности электрического тока и электрического заряда
j, ρ
замечания:
1. четвертое уравнение показывает отсутствие магнитного монополя
2.
ρ(r, t) =
X
ei δ(r − ri(t)),
3.
j(r, t) =
X
e ivi δ(r − ri(t))
Уравнения Максвелла. Общий вид
Иногда уравнения Максвелла записываются в виде
1 ∂B
∇×E = −
,
c ∂t
1 ∂D 4π
∇×H =
+
j,
c ∂t
c
∇ ⋅ D = 4πρ ,
∇⋅B = 0 .
Здесь используется запись с векторным оператором
rot A ≡ ∇ × A
div A ≡ ∇ · A
∇
:
Материальные уравнения
материальные уравнения – соотношения, описывающие отклик веществ
на внешние поля
j = σE
- форма закона Ома,
σ - удельная проводимость
D = εE
ε
- диэлектрическая проницаемость
B = µH
µ
- магнитная проницаемость
материальные уравнения можно записать, введя поляризацию (
намагниченность ( M ):
D = E + 4πP
и
P )и
H = B − 4πM
замечания:
1. в линейном случае
σ, ε, µ
зависимость ε(ω)
2. величины
3.
P = χE
, где
χ
- (линейная) восприимчивость
рассматриваются на тех же частотах, что и
называется дисперсией вещества
B, D, E
Граничные условия
•
непрерывность нормальной компоненты B
•
непрерывность тангенциальной компоненты E
•
разрыв нормальной компоненты D, определяемый плотностью
заряда на границе раздела
•
разрыв тангенциальной компоненты H, определяемый
плотностью тока на границе раздела
Вывод граничных условий
понадобятся теорема Гаусса
и теорема Стокса:
Z
Z
divAdV =
(A · n)dS
(rotA · n)dS =
Z тогда
Z
divB dV = (B · n)dS = 0
и окончательно
Z
и
Z
(A · dr)
(B1 · n 1 + B 2 · n 2)δA = 0
(B1 − B2) = 0
либо
Z
Z
Z
1
(rotE · n)dS = (E · dr) = −
(B · n)dS
c
1
и (E1 · t1 )δs 1 + (E2 · t2 )δs 2 = − (B · n)δsδh
c
и окончательно
(E 1 − E2 ) = 0
Волновое уравнение
• Общий вид волнового уравнения
(изотропная среда с поляризацией и без
свободных зарядов)
[
]
∇ 2 E + k 02 E = − k 02 P + ∇(∇ ⋅ P )
,
k 02 = ω 2 / c 2 .
• В свободном пространстве
∇ 2 E + k 02 E = 0 .
Плотность мод электромагнитного поля (1)
Рассмотрим произвольное электромагнитное поле
в кубе с ребром
L
Для компоненты поля, распространяющегося вдоль оси z
периодичность
E(z + nL) = E(z), n = 0, ±1...
периодичные граничные условия
E(z = 0) = E(z = L) = 0
разложение по плоским волнам (модам)
∞
X
E(z) =
E me ikm z
m=−∞
km =
2π
L m,
m = 0, ±1, ±2, ...
- волновые числа, принимающие
дискретные значения
Плотность мод электромагнитного поля (2)
используя разложение по плоским волнам (модам)
∞
X
E(z) =
E me ikm z
m=−∞
проинтегрируем по кубу:
ищем выражение для амплитуды моды
Z L/ 2
∞
X
−ikn z
dze
E(z) =
−L/ 2
f (km − kn ) ≡
m= −∞
Z
Em
Z
L/2
dz e− ikn ze ikmz
−L/2
L/2
− L/2
dz ei(km −k n)z = Lsinc(π(m − n)) = Lδmn
Дискретное разложение по плоским волнам
окончательно, для амплитуды моды:
∞
X
E mδ mn
m=−∞
1
≡ En =
L
Z
L/ 2
dze −ikn zE(z)
−L/ 2
В трехмерном случае: выражение для поля
E(r) =
X
E lmn ei2π(lx+my +nz)/L , l, m, n = 0, ±1, ±2, ...
lmn
а волновой вектор моды
k=
2π
L {l , m, n}
В векторном виде:
E(r, t) =
X
Ek (t)e ik·r
k
1
E k(t) =
V
Z
V
!
объем куба квантования
зависимость от времени
частота моды
E(r, t)e −ik·rdr
V = L3
exp(−iωk t)
ωk = ck
Фазовое пространство волновых векторов мод
итак, делая трехмерное преобразование Фурье
2
E(r, t) ⇒ E k(t)
2
из вещественности поля
E−k = E ∗k
расстояние между модами
в фазовом пространстве
объем фазового пространства
на одну моду
2
2π/L
(2π)3/V
Непрерывное разложение по модам:
переход к интегралу Фурье
В пределе
L→ ∞
E(r, t) =
ряд Фурье
X
k
переходит в интеграл Фурье
с фурье-амплитудами
Ek (t)e ik·r
Z
∞
V
ik·r
E(r, t) =
E(k,
t)e
dk
3
(2π) −∞
Z ∞
1
E(k, t) =
E(r, t)e−ik·r dr
V −∞
формальное правило перехода
от суммы к интегралу
P
m ...
→ (L/2π)
следует из интегрального представления дельта-функции:
Z
∞
−∞
3
R
dk
dze ikz = lim Lsinc(kL/2) = 2πδ(k)
L→∞
Число мод
Число мод поля с частотами,
меньшими
V
N(ω) = 2 ×
(2π)3
и равно
ω3V
N(ω) =
3π 2c 3
ω
объем в фазовом пространстве
(шар радиусом
k = ω/c )
объем в фазовом пространстве
на одну моду
а число мод
Z
k=ω /c
dk
k =0
4 3
4πω 3
W (ω) = πk =
3
3c 3
v = (2π)3/V
W(ω)
ω3 V
4πω3 V
N(ω) = 2 ×
· 3 = 2 3
=2·
3
v
3c
8π
3π c
Число мод и плотность мод
Число мод поля с частотами,
меньшими ω
плотность мод
число мод в интервале частот
ω
и
ω + dω
ω3V
N(ω) =
3π2c 3
D(ω) = dN(ω)/dω
ω 2V
D(ω) = 2 3
π c
отметим
D(ω) ∝ ω2
Вероятность спонтанного излучения
Энергия излучения диполя
за единицу времени
Скорость излучения фотона
с энергией
h̄ω
или
4π 2 ω2 2
U =
|d| D(ω)
3V
P = U/h̄ω
4|d| 2ω 3
P =
∝ ωD(ω)
3
3h̄c
Закон дисперсии электромагнитных волн
напоминание:
закон дисперсии
волновое число
в вакууме
в однородной среде
k(ω)
k ≡ |k| = 2π/λ
ω = ck
v = c/n