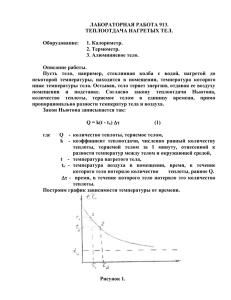
r - ТюмГАСУ

Министерство образования Российской Федерации
Тюменская государственная архитектурно-строительная академия
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ТЕПЛОТЕХНИКИ
Методические указания и
контрольные задания для студентов
специальности 100700
«Промышленная теплоэнергетика»
заочная форма обучения
Тюмень-2004
Теоретические основы теплотехники. Методические указания и контрольные
задания для студентов специальности 100700 «Промышленная
теплоэнергетика». Заочная форма обучения.
Составители: Моисеев Б.В., Степанов О.А. Тюмень, ТюмГАСА, 2004 г., стр.
Рецензент д.т.н.
профессор, член - корр. РААСН
Шаповал А.Ф.
Учебно-методический материал утвержден на заседании кафедры:
Протокол №
от « »
2004г.
Зав. кафедрой ПТ
д.т.н., профессор
О.А. Степанов
Учебно-методический материал утвержден УМС академии:
Протокол № _____ от «__»__________2004г.
Тираж 100 экземпляров
2
Содержание
Введение…………………………………………………………………………...….5
1. ЦЕЛИ И ЗАДАЧИ УЧЕБНОЙ ДИСЦИПЛИНЫ
1.1. Цели и задачи учебной дисциплины………………………………………..…..6
1.2. Общие методические указания…………………………………………………6
2. СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
2.1. Общие понятия. Первый закон термодинамики…………………….................8
2.2. Параметры идеального газа……………………………………………..…10
2.3. Второй закон термодинамики………………………………………………...10
2.4. Дифференциальные уравнения термодинамики…………………………….14
2.5. Термодинамические процессы идеальных газов…………………………….15
2.6. Реальные газы и пары. Водяной пар…………………………………….……16
2.7. Влажный воздух………………………………………………………………..17
2.8. Термодинамика потока…………………………………………………..18
2.9. Процессы компрессоров…………………………………………………….…20
2.10. Газовые циклы………………………………………………………………..21
2.11. Паровые циклы………………………………………………………………..23
2.12. Циклы холодильных установок и теплотрансформаторов………………..25
2.13. Элементы химической термодинамики…………………………………..….26
2.14. Методы непосредственного преобразования теплоты в электроэнергию...28
2.15. Основные положения теории тепломассообмена…………………………...29
2.16. Теплопроводность при стационарном тепловом режиме………………….31
2.17. Теплопроводность при нестационарном тепловом режиме…………….....32
2.18. Основные положения конвективного теплообмена………………………...34
2.19. Основы метода подобия и моделирования…………………………………35
2.20. Общие вопросы расчета конвективной теплоотдачи………………………36
2.21. Теплоотдача при вынужденном продольном омывании плоской
поверхности………………………………………………………………….37
2.22. Теплоотдача при вынужденном движении жидкости в трубах и при
поперечном смывании труб и пучков труб…………………………………39
2.23. Теплоотдача при свободном движении жидкости…………………………40
2.24. Отдельные задачи конвективного теплообмена в однородной среде……..41
2.25. Теплообмен при конденсации чистого парa……………………………..42
2.26. Теплообмен при кипении однокомпонентных жидкостей………………...44
2.27. Конвективный тепло- и массообмен…………………………………………46
2.28. Основные законы теплового излучения…………………………………..48
2.29. Теплообмен излучением между телами, разделенными
прозрачной средой………………………………………………………….49
2.30. Теплообменные аппараты…………………………………………………...50
3. СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
3.1. Общие методические указания………………………………………………..51
3.2. Тематика практических занятий………………………………………………51
3.3. Перечень лабораторных работ………………………………………………..52
4. КОНТРОЛЬНЫЕ РАБОТЫ (6 часов)
4.1. Общие методические указания………………………………………………53
3
КОНТРОЛЬНАЯ РАБОТА № 1
ЗАДАНИЕ №1 (к.р. № 1) Расчет параметров и процессов изменения
состояния идеального газа………………………………………………………..55
ЗАДАНИЕ № 2 (к. р. № 1) Расчет параметров и процессов изменения состояния
водяного пара………………………………………………………………………..58
ЗАДАНИЕ № 3 (к.р. № 1) Истечение газов и паров из сопел. Дросселирование.
Влажный воздух…………………………………………………………………..59
ЗАДАНИЕ № 4 (к.р. № 1) Процессы компрессоров…………………………………..62
Контрольные вопросы………………………………………………………..……63
КОНТРОЛЬНАЯ РАБОТА № 2
ЗАДАНИЕ № 1 (к.р. № 2) Расчет обратимого цикла газового двигателя……...68
ЗАДАНИЕ № 1* (к. р. № 2) Термодинамический анализ цикла энергетической
газотурбинной установки ГТУ - 50 – 800………………………………………..70
ЗАДАНИЕ № 2 (к. р. № 2) Расчет обратимого цикла паротурбинной
установки……………………………………………………………………………73
ЗАДАНИЕ №2 ´(к. р. № 2) Способы повышения КПД паротурбинных
установок……………………………………………………………………………..75
ЗАДАНИЕ № 2" (к.р. № 2) Термодинамический анализ циклов холодильных
установок…………………………………………………………………………….79
ЗАДАНИЕ № 3 (к. р. № 2) Расчет стационарной теплопроводности и
теплопередачи………………………………………………………………………82
ЗАДАНИЕ № 4 (к. р. № 2) Расчет нестационарной теплопроводности…………..87
КОНТРОЛЬНЫЕ ВОПРОСЫ (к. р. № 2)…………………………………………91
КОНТРОЛЬНАЯ РАБОТА №3
ЗАДАНИЕ № 1 (к. р. № 3) Расчет теплоотдачи при естественной конвекции
жидкости…………………………………………………………………………….97
ЗАДАНИЕ№ 2 (к. р. № 3) Расчет теплоотдачи при вынужденной конвекции
жидкости…………………………………………………………………………...100
ЗАДАНИЕ № 3 (к.р. № 3) Расчет теплоотдачи при фазовых превращениях….103
ЗАДАНИЕ № 4 (к. р. № 3) Теплообмен излучением……………………..105
ЗАДАНИЕ № 5 (к. р. № 3) Теплообменные аппараты……………………………108
ЗАДАНИЕ № 6 (к. р.№3) Расчет теплопередачи со сложным теплообменом на
поверхностях………………………………………………………………………112
КОНТРОЛЬНЫЕ ВОПРОСЫ (к.р. № 3)………………………………………..113
ЛИТЕРАТУРА…………………………………………………………………….118
4
ВВЕДЕНИЕ
Настоящее
пособие
предназначено для
студентов
заочников
специальности "Промышленная теплоэнергетика". При самостоятельной
работе
с
учебной
литературой
студентам необходимо добиваться
отчетливого представления о физической сущности изучаемых явлений и
процессов, особое внимание следует уделить изучению теоретических
основ теплотехники (технической термодинамике и основам тепло- и
массообмена), являющихся базой для изучения специальных дисциплин.
В конце каждой темы и раздела приведены контрольные вопросы, по
которым студент может проверить степень усвоения материала. В
методических указаниях приведены контрольные задания по разделам
"Техническая термодинамика" и "Теплопередача", которые выполняют
студенты – заочники при освоении данной дисциплины.
5
1. ЦЕЛИ И ЗАДАЧИ УЧЕБНОЙ ДИСЦИПЛИНЫ
1.1. Цели и задачи учебной дисциплины
Дисциплина "Теоретические основы теплотехники" изучается студентами
специальности "Промышленная теплоэнергетика".
Целью введения дисциплины является получение знаний по расчету, работе,
совершенствованию теплотехнического оборудования, широко используемого в
промышленности и энергетике: газотурбинных двигателей и установок,
паротурбинных установок, ядерных энергетических установок, компрессоров,
холодильного и теплообменного оборудования, тепловых насосов.
Задачей учебной дисциплины является:
• изучение основных законов термодинамики и переноса теплоты;
• изучение аналитических и экспериментальных методов исследования
процессов тепло - и массообмена;
• овладение методами расчета параметров и процессов идеального газа и
реальных рабочих тел;
• овладение количественными и качественными методами
термодинамического анализа процессов и циклов тепловых двигателей и
аппаратов с целью повышения тепловой экономичности, уменьшения
капитальных затрат, уменьшения отрицательного воздействия на
окружающую среду;
• умение произвести необходимые тепловые расчеты при проектно конструкторских, производственно - технологических, экспериментально исследовательских видах профессиональной деятельности.
1.2. Общие методические указания
Курс "Теоретические основы теплотехники" включает в себя две дисциплины: "Техническая термодинамика" и "Теплопередача". Обе дисциплины
являются
фундаментальными
в
системе
подготовки
инженеров-
теплотехников.
Техническая термодинамика
изучает закономерности превращения
энергии.
6
Теплопередача изучает законы самопроизвольного переноса теплоты.
На основе этих дисциплин осуществляется расчет и проектирование всех
тепловых двигателей - паровых и газовых турбин, реактивных и ракетных
двигателей, двигателей внутреннего сгорания, а также всевозможного
технологического оборудования - компрессоров, сушильных и холодильных
установок, тепловых насосов и т.д.
Дисциплина "Теоретические основы теплотехники" является базовой для
изучения прикладных теплотехнических дисциплин.
При изучении дисциплины рекомендуется руководствоваться программой
курса и методическими указаниями к ней, самостоятельно овладеть теорией по
учебникам и выполнить 3 контрольные работы, каждая из которых содержит
4-5 задач (обязательных) и 4 вопроса.
Ниже приводится список литературы, который включает в себя два
основных учебника [1, 4], два задачника [5, 6], справочные таблицы [2,3] а
также учебное пособие [7], которое содержит краткие теоретические основы,
необходимые для решения контрольных работ, примеры решения задач,
пояснения к решению контрольных задач и ответы на контрольные вопросы.
В задачниках [5, 6] имеются решения типовых задач, справочные данные.
Таблицы [2, 3] необходимы для нахождения параметров технически важных
газов (воздуха, азота, углекислого газа и др.) а также воды и водяного пара.
Перед выполнением контрольных работ рекомендуется прослушать обзорные лекции по основным разделам курса, которые читаются в период экзаменационных сессий. В это же время студенты выполняют лабораторно практические задания под руководством преподавателя. Цель их - более
глубокое усвоение теоретического материала и приобретение практических
навыков в проведении эксперимента.
Требования, предъявляемые на экзамене по дисциплине - знание теории и
понимание физической сущности рассматриваемых в курсе вопросов, а также
умение применить теоретические знания к решению практических задач.
7
2. СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
2.1. Общие понятия. Первый закон термодинамики
Состояние энергетики и пути ее развития. Предмет и метод термодинамики.
Техническая термодинамика как теоретическая база специальных теплотехнических дисциплин. Термодинамическая система и окружающая среда.
Термодинамическое равновесие. Неравновесные состояния и процессы.
Параметры состояния. Уравнение состояния. Термодинамическая поверхность.
Первый закон термодинамики как закон сохранения и превращения
энергии. Виды энергии. Внутренняя энергия как функция состояния. Теплота и
работа - формы передачи энергии. Работа, связанная с изменением объема.
Внешняя работа. Энтальпия. Аналитические выражения и формулировки
первого закона термодинамики.
Методические указания
При изучении темы студент должен внимательно разобраться в таких
понятиях, как термодинамическая система, рабочее тело и внешняя среда,
равновесное и неравновесное состояние рабочего тела, термодинамический
процесс. Необходимо усвоить суть таких понятий, как равновесный и
неравновесный, обратимый и необратимый термодинамические процессы; что
теплота и работа представляют собой определенные формы передачи энергии тепловую и механическую, и, что они взаимопревращаемы.
Взаимное
превращение
теплоты
и
работы
в
тепловой
машине
осуществляется с помощью рабочего тела, которое, благодаря тепловому
механическому воздействию должно обладать способностью значительно
изменять свой объем. Поэтому в качестве рабочего тела в тепловых машинах
используется газ или пар. Усвоить, что физическое состояние рабочего тела в
термодинамике определяется тремя параметрами: абсолютным давлением р,
удельным объемом υ и абсолютной температурой Т. Эти параметры связаны
между собой уравнением состояния
f(p,υ,T) = 0.
Для
понимания
физической
сути
(2.1)
изучаемых
закономерностей
термодинамики и принципов работы различных теплотехнических устройств,
8
необходимо овладеть умением графического изображения любых процессов в
термодинамических диаграммах. Необходимо уяснить, что графически можно
изображать только равновесные обратимые процессы.
Аналитическое выражение первого закона термодинамики имеет две формы:
p2
2
q
и2
и1
рd
и
q
h2
h1
dp
(2.2)
p1
1
Следует разобраться в разнице понятий "работа изменения объема" и "внешняя
работа" и уметь дать графическую интерпретацию их в диаграмме р-υ.
Необходимо уяснить принципиальную разницу между внутренней энергией,
однозначно определяемой данным состоянием рабочего тела, а также работой
и теплотой, которые появляются лишь при наличии процесса перехода
рабочего тела из одного состояния в другое, а, следовательно, зависят от
характера этого процесса.
Литература: [1, гл. 1, § 1-1, 1-2, гл. 2, § 2-1, 2-2, 2-4, 2-5].
Вопросы для самопроверки
1. Приведите определение термодинамической системы.
2. Что такое рабочее тело?
3. Какое число независимых параметров определяет состояние
рабочего тела? Почему?
4. Какие процессы называют равновесными и какие неравновесными,
обратимыми и необратимыми?
5. Какая
разница
между
термодинамическим
процессом
и
круговым
(циклом)?
6. Что такое внутренняя энергия рабочего тела?
7. Что такое теплота и работа процесса?
8. В чем сущность первого закона термодинамики?
9. Что такое энтальпия?
9
2.2. Параметры идеального газа
Уравнение состояния идеального газа. Универсальная газовая постоянная.
Нормальные физические условия. Смеси идеальных газов. Способы задания
состава
смеси.
Теплоемкость
идеальных
газов.
Истинная
и
средняя
теплоемкости. Элементы квантовой теории теплоемкости. Внутренняя энергия
и энтальпия идеальных газов.
Методические указания
Для большинства теплотехнических установок, в которых в качестве
рабочего тела используют газ, он считается идеальным. Такой газ подчиняется
уравнению состояния Менделеева - Клапейрона.
При изучении раздела о теплоемкостях обратить внимание на то, что
теплоемкость идеального газа зависит от температуры. Студент должен уметь
подсчитать теплоту с учетом зависимости теплоемкости от температуры,
пользоваться таблицами средних и истинных теплоемкостей.
Литература: [1, с. 4-19].
Вопросы для самопроверки
1. Что такое теплоемкость? Какие существуют теплоемкости?
2. В чем разница между средней и истинной теплоемкостями?
3. Как вычислить теплоемкость смеси идеальных газов при массовом
задании смеси? При объемном (мольном) задании?
4. Как вычислить среднюю теплоемкость в интервале температур от 0 до 1?
5. Как рассчитать теплоту процесса через средние теплоемкости от 0 до 1?
6. Как определяют газовую постоянную смеси идеальных газов, заданную
объемными долями?
2.3. Второй закон термодинамики
Формулировки второго закона термодинамики. Обратимые и необратимые
процессы. Основные причины необратимости процессов. Термодинамические
циклы: прямые и обратные, обратимые и необратимые. Термический
коэффициент полезного действия цикла теплового двигателя. Прямой цикл
Карно и его КПД. Обратный цикл Карно и его холодильный коэффициент.
Теорема Карно. Максимальная работа цикла. Доказательство существования
10
энтропии. Термодинамические процессы и циклы в T-s- диаграмме. Среднеинтегральная температура подвода (отвода) теплоты и эквивалентный цикл
Карно. Возрастание энтропии при необратимых процессах. Аналитическое
выражение второго закона термодинамики для необратимых процессов. Необратимая адиабата. Теплообмен с конечной разностью температур. Возрастание энтропии изолированной системы. Статистический смысл второго закона
термодинамики. Энтропия и термодинамическая вероятность состояния.
Эксергия как мера работоспособности системы. Эксергия массы вещества в
объеме, потока тепла и потока вещества. Потеря эксергии при необратимых
процессах. Эксергетический КПД.
Энтропийный метод расчета потерь
энергии необратимых процессов.
Методические указания
Первый закон термодинамики указывает лишь на количественную сторону
взаимопревращения теплоты и работы, но он не отвечает на вопрос: каковы
условия взаимного перехода различных видов энергии? Опыт показывает, что в
теплоту
любой
вид
энергии
может
переходить
самопроизвольно,
а
преобразование в замкнутом процессе теплоты целиком в работу невозможно.
Действительно, проинтегрировав выражение
ds
dq
T ,
(2.3)
ds
dq
.
T
(2.4)
по замкнутому контуру, получим
Но так как ds
0 , поскольку s - функция состояния, то
dq
T
Учитывая, что
dq
T
0,
0.
(2.5)
тогда и только тогда, когда q на отдельных участках
цикла меньше нуля, т.е., наряду с подводом теплоты в цикле должны быть
процессы и с отводом теплоты. Но это и означает, что полностью подведенную
11
теплоту в цикле нельзя превратить в работу.
Все самопроизвольные процессы в природе односторонни: вода сама по себе
течет лишь с гор на равнины, электрический ток распространяется по проводу
от большего потенциала к меньшему, теплота передается от горячего тела к
холодному. Можно, конечно, заставить протекать эти процессы в обратном
направлении, но для этого необходима компенсация. В тепловом двигателе, в
котором происходит несамопроизвольный процесс превращения теплоты в
работу, компенсирующим самопроизвольным процессом является переход
теплоты от теплоотдатчика к теплоприемнику. В холодильных машинах переход
теплоты от холодного тела к горячему компенсируется затратой работы.
Термический КПД любого цикла можно выразить через средне-интегральные
температуры процессов подвода и отвода теплоты Т' и Т" в виде
T
T
1
t
.
(2.6)
Эта формулировка показывает, что при выбранных минимальной и максимальной температурах холодильника и источника теплоты наивысшее
значение
t
достигается, когда T"=Tмин=const и T'=Tмакс=const, т.е. при изо-
термическом подводе и отводе теплоты. Такой цикл (цикл Карно) имеет первостепенное значение в термодинамике, являясь, по существу, выражением
второго закона термодинамики. При изучении второго закона термодинамики
студент встречается с функцией состояния - энтропией. Изменение энтропии
рабочего тела в элементарном процессе определяется по формуле
s
q
T
,
(2.7)
где q - количество теплоты, участвующего в процессе; Т - абсолютная температура рабочего тела. Из формулы следует, что так как всегда Т>0, то знак Δs
совпадает со знаком q: при подводе теплоты (q>0) энтропия тела возрастает
(Δs>0), а при отводе (q<0) - убывает (Δs<0).
Рассмотрим изменение энтропии простейшей системы, состоящей из
источника теплоты с температурой Ти и газа с температурой Тг. Изменение
12
энтропии такой системы запишется в виде
s
sи
q
Tи
sГ
q
TГ
q
1
TГ
1
Ти .
(2.8)
Для обратимых процессов Тг= Ти, очевидно Δs=0. Если рассматривается
система, состоящая из холодильника с температурой Тх и газа с температурой
Тr, то получаем
s
q
1
Tx
1
TГ
и
Δs>0,
(2.9)
где знак > относится к необратимым процессам. Таким образом, если для
отдельного тела энтропия может увеличиваться (при q>0), уменьшаться (при
q<0) или оставаться без изменения (при q=0), то для изолированной системы
она может или расти (необратимый процесс), или оставаться постоянной
(обратимый процесс). Важно усвоить, что рост энтропии изолированной
системы
связан
с
неизбежным
уменьшением
ее
работоспособности.
Максимально возможная работа, которую можно получить за счет теплоты,
если холодильником является окружающая среда, называется эксергией этой
теплоты.
Введение
понятия
эксергии
теплоты
дает
возможность
количественно оценить потерю работоспособности за счет необратимости
процессов. Разность между подводимой к системе эксергией и отводимой от
нее характеризует потери эксергии. Поэтому степень необратимости
процессов можно характеризовать эксергетическим КПД
экс
ехотв
ехподв
или
экс
1
ехпот
,
ехподв
(2.10)
где ехподв, ехотв, - подводимая и отводимая эксергия, Δехпот=ехподв – ехотв - потеря
эксергии.
Применимость второго закона термодинамики ограничена земным опытом.
Распространение его на Вселенную, как сделал Клаузиус, приводит к
неправильным
выводам.
Клаузиус,
рассматривая
Вселенную
как
изолированную систему, в которой все процессы необратимы, сделал вывод,
что "энтропия Вселенной стремится к максимуму", и отсюда, как следствие 13
"тепловая
смерть
Вселенной".
Несостоятельность
теории
Клаузиуса
"тепловой смерти" Вселенной имеет также и другие обоснования:
а)дифференциальные соотношения термодинамики несправедливы для
микромира, в котором расстояния между частицами материи сравнимы с
дифференциалом исследуемого объема;
б) решения дифференциальных уравнений зависят от конкретных
условий на границе исследуемой области, но на границе бесконечной
Вселенной эти условия неизвестны.
Вопросы для самопроверки
1. Что такое термодинамический цикл?
2. В чем состоят термическая и механическая необратимости
процессов?
3. Что такое прямой и обратный циклы Карно?
4. Что называется термическим КПД и холодильным коэффициентом
произвольного цикла? Чему они равны для цикла Карно?
5. Почему обратный цикл Карно является самым эффективным среди
других циклов, осуществляемых в заданном интервале температур?
6. В чем сущность второго закона термодинамики?
7. Приведите аналитическое выражение второго закона термодинамики
для обратимых и необратимых процессов.
8. Как изменяется энтропия изолированной системы при протекании в
ней обратимых и необратимых процессов?
9. Что такое эксергия?
10.Чем определяется уменьшение работоспособности изолированной
системы?
2.4. Дифференциальные уравнения термодинамики
Основные дифференциальные уравнения термодинамики. Связь между
термическими и калорическими величинами в переменных υ, Т и р, Т.
Энергии Гиббса и Гельмгольца и их свойства. Зависимость теплоемкостей ср и cv
от объема и давления. Уравнения Максвелла.
14
Методические указания
Дифференциальные уравнения термодинамики являются теоретическим
фундаментом для развития термодинамики как науки. По известному
уравнению состояния газа с помощью дифференциальных связей можно
найти зависимость теплоемкостей с р и cv от давления и объема.
Дифференциальные связи позволяют выражать одни термодинамические
функции через другие, в частности, получить дифференциальные уравнения,
связывающие калорические параметры (u, h, s) и термические (р, υ, Т). С их
помощью, используя эксперимент, определяется физическая сущность
явлений и процессов, протекающих в природе. Студент должен усвоить
методику
получения
основных
дифференциальных
соотношений
термодинамики и способы их применения.
Литература: [1, с. 102-108].
2.5. Термодинамические процессы идеальных газов
Термодинамические процессы изменения состояния идеальных газов.
Общие вопросы исследования процессов изменения состояния идеального газа:
изохорного,
изобарного,
изотермического,
адиабатного.
Политропные
процессы. Основные термодинамические процессы как частный случай
политропного процесса. Определение показателя политропы и теплоемкости
политропного
процесса.
Определение
теплоты
и
работы
процесса.
Изображение процессов в р-υ и T-s -диаграммах.
Методические указания
Общий
метод исследования
термодинамических
процессов является
универсальным. Он не зависит от природы рабочего тела. Метод базируется на
применении
уравнений
первого
и
второго
законов
термодинамики,
справедливых для любых рабочих тел:
s2
q
u2
u1
,
q
h2
h1
q
w,
Tds ,
(2.11)
s1
p2
v2

pdv ,
v1
w
vdp .
(2.12)
p1
15
На основании этих уравнений можно определить теплоту и работу любого
термодинамического
процесса.
Студенту
необходимо
уяснить
понятие
политропного процесса, под которым понимается любой термодинамический
процесс идеального газа с постоянной теплоемкостью сn (или показателем
политропы п) в этом процессе. Уяснить общность политропного процесса,
выраженного уравнением pυn=const, получить из него уравнения основных
процессов (изохорного, изотермического, изобарного, адиабатного). Знать
определение показателя политропы п и теплоемкости политропного процесса сn,
как обобщающих величин, из которых получаются частные значения их для
основных процессов.
Литература: [1, с. 32-36].
Вопросы для самопроверки
1.Основная задача расчета любого термодинамического процесса.
2.Изобразите в р-υ и T-s -диаграммах изохорный, изобарный, изотермический,
адиабатный процессы идеального газа.
3.Охарактеризуйте каждый из этих процессов. Чему равен показатель политропы
и теплоемкость в каждом из этих процессов?
4.Как
определяют
теплоту
изохорного,
изобарного,
изотермического,
адиабатного и политропного процессов идеального газа?
2.6. Реальные газы и пары. Водяной пар
Термодинамические свойства реальных веществ, р-υ и T-s -диаграммы.
Уравнение
Ван-дер-Ваальса.
Критическое
состояние.
Парообразование
и
конденсация. Степень сухости. Теплота фазового перехода. Плавление. Сублимация. Тройная точка. Уравнение Клапейрона - Клаузиуса. Аномалии воды.
Удельный объем, энтальпия, энтропия жидкости, влажного, сухого насыщенного и
перегретого
пара.
Сверхкритическая
область
состояния
пара.
Таблицы
термодинамических свойств воды и водяного пара. T-s и h-s — диаграммы
водяного пара. Расчет процессов изменения состояния водяного пара по таблицам
и диаграммам.
16
Методические указания
Водяной пар является рабочим телом в современных теплосиловых установках, а также находит применение в различных технологических процессах.
Необходимо разобраться с процессами воды и водяного пара и уметь
изображать их в р-υ, T-s и h-s -диаграммах. Параметры воды и водяного пара
можно определить по таблицам и диаграммам. В области перегретого пара и на
кривой сухого насыщенного пара по диаграмме можно определить параметры р,
υ, Т, h, s; в области влажного пара определяется в дополнение к выше
перечисленным еще и степень сухости х<1. Необходимо научиться схематично
изображать основные процессы (изохорный, изобарный, изотермический,
адиабатный) в p-υ, T-s и h-s -диаграммах.
Литература: [1, с. 160-198].
Вопросы для самопроверки
1.Изобразите процесс парообразования в р-υ, T-s и h-s-диаграммах.
2.В чем состоит цель расчета термодинамических процессов воды и водяного
пара?
3.Изобразите в p-υ, T-s и
h-s - диаграммах основные термодинамические
процессы водяного пара.
4.Как определяют теплоту и работу для основных термодинамических
процессов водяного пара?
2.7. Влажный воздух
Основные
определения.
Абсолютная
и
относительная
влажность.
Температура точки росы. Влагосодержание. Газовая постоянная и плотность
влажного воздуха, h-d -диаграмма влажного воздуха. Термодинамические
процессы с влажным воздухом (охлаждение, нагрев, смешение, сушка нагретым
воздухом) и др. Психрометр, гигрометр.
Методические указания
Усвоить основные понятия и определения, относящиеся к влажному воздуху.
Уметь определять параметры влажного воздуха и производить расчет
процессов.
Приобрести
навыки
в
пользовании
таблицами
и
h-d -диаграммой влажного воздуха.
17
Литература: [1, с. 371-378].
Вопросы для самопроверки
1.Приведите определение влажного воздуха.
2.Что такое абсолютная, относительная влажность, влагосодержание?
3.В каких пределах может изменяться влагосодержание?
4.Что такое точка росы?
5.Как изображают основные процессы влажного воздуха
диаграмме?
2.8. Термодинамика потока
Истечение и дросселирование газов и паров. Уравнение первого закона
термодинамики для потока и его анализ. Адиабатное истечение. Скорость
адиабатного истечения.
Параметры полного адиабатного торможения потока. Сопло и диффузор.
Скорость истечения газа из суживающегося сопла. Максимальный расход и
критическая скорость. Критическое отношение давлений и температур.
Зависимость скорости и расхода от отношения начального к конечному
давлению. Комбинированное сопло Лаваля. Расчет истечения водяного пара.
Истечение с учетом необратимости. Коэффициенты скорости и потери энергии.
Смешение потоков газов и паров.
Сущность процесса дросселирования. Дросселирование идеального газа.
Изображение процесса дросселирования в h-s - диаграмме. Потеря эксергии
потока при дросселировании. Дифференциальный и интегральный температурный эффект адиабатного дросселирования реальных газов. Температура
инверсии. Кривая инверсии.
Методические указания
Уравнение первого закона термодинамики для потока является основой,
на которой строится вся теория истечения. Необходимо разобраться в физическом смысле отдельных членов уравнения первого закона термодинамики.
Представлять себе, почему в суживающихся цилиндрических каналах скорость потока не может превзойти скорости звука; в каких случаях следует
делать сопло сужающимся, а в каких - расширяющимся; уметь анализиро18
вать изменение параметров рабочего тела при движении его по соплу Лаваля. Понять принципиальную разницу в расчете скорости истечения идеального газа и водяного пара. Нужно твердо усвоить, что аналитические зависимости, выведенные для идеального газа, неприменимы для реального газа,
а тем более для пара. Скорость истечения пара и реального газа следует рассчитывать по формуле:
С2
2 h1 h2 ,
(2.13)
где h1 и h2 - значения энтальпии, в Дж/кг. Необходимо отчетливо представлять себе влияние трения на адиабатный процесс истечения идеального газа
и водяного пара и уметь изображать реальный процесс истечения в
T-s и h-s -диаграммах. При изучении адиабатного процесса дросселирования
следует обратить внимание на то, что при дросселировании перепад давлений
расходуется на преодоление сил трения, а увеличением кинетической энергии
газа можно пренебречь, т.е.
vdp d тр .
(2.14)
При этом условии, как следует из первого закона термодинамики, энтальпия
начала и конца процесса дросселирования одинакова (hi = h2). Но процесс
дросселирования нельзя отождествлять с процессом, протекающим при
постоянной энтальпии. Уяснить разницу между адиабатным дросселированием
и адиабатным процессом, при котором dq=0 и ds=0. Понять, почему в
результате дросселирования реального газа температура его может уменьшаться,
увеличиваться или оставаться неизменной.
Литература: [1, с. 229-21 1; 203-21 1].
Вопросы для самопроверки
1. Какие допущения лежат в основе вывода уравнения первого закона
термодинамики для потока?
2. Объясните физический смысл каждого члена уравнения первого закона
термодинамики для потока.
3. На что расходуется работа расширения газа в потоке?
4. Что такое сопло и диффузор?
19
5. Какая связь между изменением профиля канала и изменением скорости
адиабатного течения рабочего тела?
6. Как вычислить действительную скорость истечения газа на выходе
из сопла?
7. Какой процесс называется дросселированием?
8. Где используется процесс дросселирования?
9. Как изменяется температура реального газа при дросселировании?
2.9. Процессы компрессоров
Компрессор. Работа, затрачиваемая на привод компрессора. Изотермическое,
адиабатное
и
политропное
сжатие.
Многоступенчатый
компрессор.
Оптимальное распределение давлений по ступеням. Изображение в р- υ и T-s диаграммах процессов в компрессорах для одно- и двухступенчатого сжатия.
Определение эффективной мощности, затрачиваемой на привод компрессора и
отводимой при охлаждении теплоты. Понятия эксергетического, внутреннего
относительного, изотермического КПД компрессора.
Методические указания
Ознакомившись с конструктивной схемой и работой поршневых компрессоров, необходимо обратить внимание на то, что процессы всасывания и
выталкивания, изображенные на индикаторной диаграмме, не являются изобарными, т.к. в этих процессах не происходит изменения состояния, а меняется
только количество всасываемого и выталкиваемого рабочего тела. Обратить
внимание, что на конечную температуру в конце сжатия и на работу привода
компрессора значительно влияет показатель политропы сжатия. Необходимо
уделить внимание изображению термодинамических процессов в р- υ и T-s диаграммах. В связи с применением высокого давления в некоторых
технологических аппаратах, необходимо разобраться в принципах работы
многоступенчатых компрессоров.
Литература: [4, с. 220-357].
20
Вопросы для самопроверки
1. Назначение компрессоров.
2. Принцип действия поршневого компрессора и изображение работы
компрессора в р-υ -диаграмме.
3. Какой процесс сжатия наиболее выгодный?
4. Можно ли получить газ высокого давления в одноступенчатом компрессоре?
5. Как определяется работа, затрачиваемая на привод компрессора?
6. Чем вызвано применение нескольких ступеней сжатия в многоступенчатом
компрессоре?
7. Как определяется эффективная мощность, затрачиваемая на привод
компрессора?
8. Как определяется внутренний относительный КПД компрессора?
9. Расчет отводимой теплоты при охлаждении компрессора.
2.10. Газовые циклы
Циклы двигателей внутреннего сгорания. Циклы с подводом тепла при
постоянном давлении, при постоянном объеме, со смешанным подводом тепла.
Сравнение циклов по термическому КПД. Зависимость термического КПД от
средних температур подвода и отвода теши. Расход тепла и топлива,
эффективный КПД двигателя внутреннего сгорания.
Циклы газотурбинных двигателей и установок. Схема и цикл газотурбинной
установки с подводом тепла при постоянном давлении. Термический КПД
обратимого цикла. Действительный цикл газотурбинной установки и система
КПД для оценки потерь в ней. Влияние степени повышения давления воздуха в
компрессоре на термический КПД цикла, на эффективный КПД установки.
Методы повышения КПД: применение регенерации тепла, многоступенчатого
сжатия воздуха в компрессоре и ступенчатого расширения продуктов сгорания в
турбине. Замкнутые циклы газотурбинных установок. Циклы воздушно —
реактивных и ракетных двигателей.
21
Методические указания
При термодинамическом исследовании циклов ДВС делается допущение о
применимости в качестве рабочего тела идеального газа с постоянной
теплоемкостью, а также допущение о термодинамической обратимости процессов, составляющих цикл. В двигателях внутреннего сгорания осуществляются циклы с подводом теплоты при постоянном объеме, с подводом теплоты
при постоянном давлении и цикл со смешанным подводом теплоты.
Необходимо уметь изобразить любой цикл в р- υ и T-s -диаграммах, определить
подведенную и отведенную теплоту, работу и термический КПД цикла. При
сравнении тепловой экономичности рассматриваемых циклов при одинаковых
степенях сжатия наиболее экономичным будет цикл с изохорным подводом
теплоты. Если же сравнение тепловой экономичности производить при
одинаковых максимальных давлениях, то максимальный КПД имеет цикл с
изобарным подводом теплоты, а наименьший - цикл с изохорным подводом
теплоты.
При изучении циклов газотурбинных установок обратить внимание на
преимущества их перед поршневыми ДВС. Необходимо разобраться в принципе
работы газотурбинных установок, знать схемы установок, уметь анализировать
их работу, используя диаграммы р- υ и T-s.
Уметь вычислить термический КПД обратимого цикла, внутренний КПД
действительного цикла, эффективный КПД газотурбинной установки. Обратить
внимание на физический смысл этих КПД. Помнить, что термический
коэффициент полезного действия повышается за счет введения регенерации
теплоты, ступенчатого сжатия и ступенчатого подвода теплоты.
Литература: [1, с. 264-285; с. 252-258].
Вопросы для самопроверки
1. Назовите три основных вида циклов поршневых двигателей внутреннего
сгорания.
2. Изобразите цикл ДВС с подводом теплоты при и - const в р- υ и T-s диаграммах.
3. Как вычислить количество теплоты, отводимой от рабочего тела и
22
термический КПД цикла с подводом теплоты при υ = const?
4. Изобразите цикл ДВС с подводом теплоты при р= const в р- υ и T-s диаграммах.
Как
вычисляется
подведенная
и
отведенная
теплота,
термический КПД такого цикла?
5. Изобразите цикл ДВС со смешанным подводом теплоты в р- υ и T-s диаграммах. Как
определяется подведенная и отведенная теплота и
термический КПД такого цикла?
6. Какие преимущества имеют газотурбинные установки по сравнению
с двигателями внутреннего сгорания?
7. Приведите принципиальную схему и цикл ГТУ в р- υ и T-s —
диаграммах с подводом теплоты при р = const.
8. Как вычислить термический КПД обратимого цикла, внутренний
КПД действительного цикла газотурбинной установки?
9. Что называется эффективным КПД газотурбинной установки и как
он определяется?
10.Назовите методы повышения термического КПД в газотурбинных
установках.
2.11. Паровые циклы
Циклы
паротурбинных
установок.
Принципиальная
схема
и
теоретический цикл ПТУ. Влияние начальных и конечных параметров пара на
термический КПД. Действительный цикл ПТУ. Система КПД для оценки
потерь в паротурбинной установке. Уравнение теплового и эксергетического
балансов. Понятия эксергетических КПД турбины, парового котла. Удельные
расходы пара, тепла и топлива.
Промежуточный перегрев пара и причины его применения. Схема ПТУ с
промежуточным перегревом в T-s -диаграмме, термический КПД обратимого
цикла.
Регенеративные циклы. Схема и цикл ПТУ в T-s -диаграмме с
регенеративным подогревом питательной воды в подогревателях воды за счет
тепла отборов пара из турбины. Термический КПД регенеративного цикла.
Зависимость термического КПД от числа отборов.
23
Комбинированные циклы. Преимущества и недостатки водяного пара как
рабочего тела. Бинарный цикл и его КПД. Парогазовый цикл и его КПД.
Схемы и циклы теплофикационных паротурбинных установок.
Циклы атомных электростанций.
Методические указания
При изучении темы следует уделить внимание основному циклу
паротурбинной установки - циклу Ренкина. В этом цикле осуществляется
полная конденсация рабочего тела в конденсаторе, поэтому для подачи
питательной воды в паровой котел используется питательный насос, который
имеет малые габариты и высокий КПД по сравнению с громоздким
малоэффективным
компрессором.
Исследование
основного
цикла
осуществляется с помощью p- υ, T-s и h-s -диаграмм. Необходимо уметь
анализировать циклы с помощью диаграмм, разобраться в выводе уравнения
для определения термического КПД цикла Ренкина. Уяснить, что рост КПД
паротурбинной установки возможно осуществить за счет изменений в самом
цикле:
введения
промежуточного
перегрева
пара,
использования
регенеративных, парогазовых и бинарных циклов. Литература: [1, с. 293-323].
Вопросы для самопроверки
1. Приведите принципиальную схему паротурбинной установки.
2. Изобразите обратимый цикл Ренкина в р- υ, T-s и h-s -диаграммах.
3. В чем отличие цикла Ренкина от цикла Карно?
4. Как определить термический КПД цикла Ренкина?
5. Как и почему изменяется КПД цикла Ренкина при увеличении
начальных параметров водяного пара?
6. Каково влияние давления в конденсаторе на величину термического
КПД цикла Ренкина?
7. Как изменяется влажность пара в конце адиабатного расширения
при повышении начального давления,
если
начальная
температура
и
конечное давление пара остаются неизменными?
8. Для
каких
целей
в
паротурбинной
установке
используют
24
промежуточный перегрев пара?
9. В
чем
состоит
выгодность
регенеративного
цикла
паротурбинной
КПД
паротурбинной
установки?
10.Что
такое
внутренний
относительный
установки, как его определяют?
11.В
чем
преимущество
комбинированной
выработки
теплоты
и
электроэнергии?
12.Как определяют удельный расход пара в паротурбинной установке?
13.Как определяют эффективный КПД паротурбинной установки?
14.В чем состоят преимущества парогазовых циклов?
2.12. Циклы холодильных установок и теплотрансформаторов
Обратный цикл Карно. Холодильный коэффициент и эксергетический КПД.
Требования, предъявляемые к рабочим телам холодильных установок. Схема и
теоретический цикл газовой холодильной установки. Способы увеличения
эксергетического КПД и холодопроизводительности. Принципиальная схема
и цикл парокомпрессионной холодильной установки.
Пароэжекторная холодильная установка. Абсорбционная холодильная
установка. Принципиальные схемы и изображение циклов в р - υ, и T-s диаграммах.
Принципиальная схема теплового насоса. Понятие о коэффициенте
теплоиспользования.
Методические указания
При изучении циклов различных холодильных установок нужно обратить
внимание на то, что как для тепловых двигателей, так и для холодильных
машин эталоном является цикл Карно. Термический КПД любого цикла
сравнивается с КПД цикла Карно в этих же пределах температур. Для холодильных установок холодильником является внешняя атмосфера или вода, у
которой температура ниже температуры холодильника, а источником теплоты содержимое холодильной камеры, у которого температура выше хладоагента.
Поэтому эквивалентным циклом Карно для холодильной установки будет цикл,
25
осуществляемый между температурами холодильника (воздух, вода) и
источника (охлаждаемый объем холодильной камеры). Знание классификации и
принципиальных схем холодильных установок позволяет правильно выбирать
соответствующий тип холодильной установки. Усвоив учебный материал,
студент сможет анализировать с помощью T-s- диаграммы работу и расчеты
этого
цикла.
применяется
В
паровой
компрессионной
расширительный
цилиндр
холодильной
(детандер),
а
установке
рабочее
не
тело
дросселируется в регулировочном вентиле. Это ведет к потере холодопроизводительности, но, упрощая установку, позволяет легко регулировать
давление пара и получать низкую температуру в охладителе. Тепловые насосы
также работают по обратному циклу. В них теплота, забираемая от окружающей среды, с помощью затраченной работы повышает энергетический
уровень рабочего тела и при более высокой температуре отдается внешнему
потребителю. Необходимо понять принципиальную схему и работу теплового
насоса и уяснить понятие коэффициента теплоиспользования.
Литература: [4, с. 344-367].
Вопросы для самопроверки
1.Классификация холодильных установок.
2.Что называется холодильным коэффициентом?
3.Приведите принципиальную схему воздушной холодильной установки и
опишите ее работу.
4.Изобразите идеальный цикл воздушной холодильной установки и
опишите процессы, осуществляемые в ней.
5.Приведите принципиальную схему работы паровой компрессионной
холодильной установки и опишите ее работу.
6.Чем отличается работа теплового насоса от работы холодильных установок?
2.13. Элементы химической термодинамики
Первый закон термодинамики в термохимии. Тепловой эффект реакции.
Закон Гесса и его следствия. Зависимость теплового эффекта реакции от
температуры. Стандартный тепловой эффект. Второй закон термодинамики в
термохимии. Закон действующих масс. Степень диссоциации. Термодина26
мические свойства диссоциирующих газов. Константа равновесия и максимальная работа реакции. Зависимость константы равновесия от давления и
температуры. Тепловая теорема Нернста. Абсолютная энтропия. Стандартные
значения термодинамических функций веществ.
Методические указания
При изучении настоящей темы следует обратить внимание на сходство
математических выражений, описывающих первый закон термодинамики для
физических и химических процессов изменения состояния, на различие в
тепловом эффекте реакции, возникающем в зависимости от того, идет ли
процесс при p=const или при υ=const.
Весьма существенным для усвоения материала данной темы является
правильное понимание закона Гесса, устанавливающего независимость теплового эффекта химической реакции от ее промежуточных стадий.
Необходимо разобраться в таких фундаментальных понятиях, как химически
обратимые и необратимые реакции, причем химическую обратимость не
следует смешивать с термодинамической обратимостью.
При изучении приложения второго закона термодинамики к химическим
процессам следует хорошо разобраться в существе характеристических функций
и их свойствах, а также усвоить понятие максимальной работы.
Для понимания равновесия химических реакций чрезвычайно важно разобраться в законе действующих масс.
Очень существенна с принципиальной точки зрения так называемая тепловая теорема Нернста, следствием которой является возможность вычисления
абсолютного значения энтропии и свободной энергии.
Литература: [1, гл. 15, с. 382 - 407].
Вопросы для самопроверки
1. В чем смысл и практическое значение закона Гесса?
2. Что такое константа равновесия и в чем ее практическое значение?
3. Что такое обратимая и необратимая химические реакции?
4. Что такое максимальная полезная работа реакции?
5. В чем сущность закона действующих масс?
27
6. Как влияет температура на константу равновесия, на скорость химической
реакции?
7. Что такое эндотермическая и экзотермическая реакции?
8. Сущность тепловой теоремы Нернста и ее практическое значение.
2.14. Методы непосредственного преобразования теплоты в
электроэнергию
Методы непосредственного преобразования теплоты в электроэнергию.
Схема, цикл и КПД установки с магнитогидродинамическим генератором.
Термоэлектрические генераторы и их КПД. Термодинамические основы
преобразования энергии в топливных элементах.
Методические указания
При изучении раздела "Паротурбинные установки" было установлено, что
термический КПД цикла даже самой совершенной схемы не превышает
45 - 50% теплоты сжигаемого топлива, т.е. 55 - 50 % теплоты рассеивается в
окружающую среду. Поэтому понятно стремление изыскать такие способы
получения электроэнергии, которые позволили бы существенно повысить
эффективность процесса. Наиболее перспективным для крупной энергетики
является способ преобразования энергии топлива в электроэнергию, осуществляемый в МГД — генераторах с последующим использованием тепла отходящих газов из генератора в паросиловом цикле. Необходимо уяснить, что
повышение при этом общего термического КПД установки до 65 - 70% обусловлено использованием большего температурного интервала, чем в обычном
паросиловом цикле, за счет повышения начальной температуры рабочего тела
(1500°С и выше).
Большой интерес представляет способ преобразования энергии в термоэлектрических генераторах, термоэлектронных преобразователях и электрохимических генераторах. В последних, даже в реальных условиях, КПД может
быть получен близким к единице.
Следует разобраться в термодинамических основах процессов прямого
преобразования энергии рабочего тела в электроэнергию и представлять себе
принцип действия установок, в которых протекают эти процессы.
Литература: [I, гл. 12, с. 325 - 344].
28
Вопросы для самопроверки
1.Что положено в основу принципа работы МГД - генератора?
Почему при пользовании МГД — генератора можно получить высокие
значения КПД?
3.Опишите схему и цикл установки с МГД - генератором.
4.На каком принципе основана работа термоэлектрических генераторов?
5.От чего зависит КПД термоэлектрических генераторов и каково его
примерное значение?
6.На каком принципе основана работа термоэлектронного преобразователя?
7.Что называют топливным элементом?
8.Принцип действия топливного элемента.
9.Какой максимальный КПД можно получить в топливном элементе и почему?
2.15. Основные положения теории тепломассообмена
Введение. Основные понятия и определения теории тепломассообмена.
Предмет и задачи теории теплообмена. Основные процессы передачи теплоты и
массы. Виды переноса теплоты: теплопроводность, конвекция, излучение.
Теплоотдача. Теплопередача. Макроскопический характер учения о теплоте.
Современные проблемы тепломассообмена. Вклад отечественных ученых в
развитие тепломассообмена.
Инженерные методы расчета видов теплопереноса. Основные понятия и
определения теплопроводности. Закон Фурье. Коэффициент теплопроводности.
Механизм передачи теплоты в металлах, диэлектриках, жидкостях и газах.
Теплопроводность однослойной и многослойной плоских и цилиндрических
стенок. Основные понятия и определения конвективного теплообмена. Закон
Ньютона - Рихмана. Коэффициенты теплоотдачи и теплопередачи. Теплообмен
излучением. Понятие о сложном теплообмене.
Методические указания
В результате изучения этой темы студент должен получить представление о
теплопроводности как об одном из трех элементарных процессов теплообмена.
Следует усвоить понятие «температурное поле» и такую важнейшую
характеристику как температурный градиент, от которого зависит ин29
тенсивность теплообмена в теле. Необходимо обратить внимание, что из
всевозможных видов температурных полей простейшими, наиболее удобными
для расчета, являются одномерные температурные поля (плоское, цилиндрическое и сферическое), в которых температура, а, следовательно, и ее
градиент зависят только от одной координаты. Именно одномерные поля
наиболее наглядно изображаются графически. При этом необходимо освоить
способы представления температурного поля: аналитическое (в виде формул),
графическое (в виде изотерм в координатах «температура - расстояние») и
табличное. Нужно усвоить понятия «плотность теплового потока» и «тепловой
поток», их единицы; обратить внимание на то, что единицами теплового потока
являются единицы мощности [ватты (Вт)].
При изучении дифференциального уравнения теплопроводности Фурье
необходимо обратить внимание, что его вывод основан на законе сохранения
энергии, на законе теплопроводности Фурье и на допущении о постоянном
значении коэффициента теплопроводности, которые и определяют существо
этого уравнения и область его применения.
Вопросы для самопроверки
1. Могут ли изотермические поверхности пересекаться?
2. Могут ли изотермические поверхности быть замкнутыми?
3. Из двух противоположных утверждений (grad t перпендикулярен изотерме;
grad t параллелен изотерме) выберите правильное.
4. Могут ли быть одинаковыми истинная и средняя плотности теплового
потока?
5. Могут ли быть выражены в одинаковых единицах плотность теплового
потока и объемная мощность внутренних источников теплоты?
6. Можно ли рассматривать дифференциальное уравнение теплопроводности
Фурье как одну из форм закона сохранения энергии?
7. Входят ли физические параметры тела в состав условий однозначности,
необходимых для решения дифференциального уравнения теплопроводности?
8. Тождественны
ли понятия "условия однозначности"
и
"граничные
условия"?
30
2.16. Теплопроводность при стационарном тепловом режиме
Передача теплоты через однослойную и многослойную плоские стенки при
граничных условиях I и III рода. Распределение температур при постоянном и
переменном коэффициентах теплопроводности. Коэффициент теплопередачи.
Передача теплоты через однослойную и многослойную цилиндрические стенки
при граничных условиях I и III рода. Линейный коэффициент теплопередачи.
Критический диаметр изоляции. Передача теплоты через шаровую стенку.
Теплопроводность в стержне (ребре) постоянного поперечного сечения.
Теплопередача через плоскую ребристую стенку. Способы интенсификации
процессов теплопередачи. Связь способов интенсификации с современными
проблемами экономии материальных и энергетических ресурсов и повышением
экономичности производства. Теплопроводность в неограниченной плоской
стенке и круглом стержне в случае постоянного коэффициента теплопроводности при наличии внутренних источников теплоты. Теплопроводность в неограниченной цилиндрической стенке при наличии внутренних
источников теплоты и: а) отводе теплоты через наружную поверхность, б)
отводе теплоты через внутреннюю поверхность, в) отводе теплоты через
наружную и внутреннюю поверхности.
Литература [4, гл.2, § 2.1 - 2.4,2.6 - 2.8, 2.13]
Методические указания
Поскольку производные вдоль изотермических поверхностей обращаются в
нуль, написание уравнения Фурье существенно упрощается в случаях
одномерных температурных полей. Однако при выводе формулы теплопроводности плоской стенки с переменным коэффициентом теплопроводности
дифференциальное уравнение Фурье неприменимо, и в выводе используется
непосредственно закон Фурье при условии постоянства плотности теплового
потока.
Вопросы для самопроверки
1.Верно ли, что при стационарном режиме теплообмена перепад температур на
стенке прямо пропорционален ее термическому сопротивлению?
2.Одинаковую ли размерность имеют плотность теплового потока и
31
линейная плотность теплового потока?
3.Одинаковы ли по своим размерностям термические сопротивления удельное для плоской стенки и линейное для цилиндрической стенки?
4.Верно ли, что в случае плоской стенки удельное термическое сопротивление
теплоотдачи
(пограничного
слоя)
зависит
только
от
коэффициента
теплоотдачи?
5.Верно ли, что в случае цилиндрической стенки линейное термическое
сопротивление
теплоотдачи
(пограничного
слоя)
зависит
только
от
коэффициента теплоотдачи?
6.Можно ли вычислить критический диаметр цилиндрической стенки,
не учитывая условий теплообмена ее внешней поверхности с окружающей
средой?
7.Если на двух плоских стенках одинаковой толщины наблюдается
одинаковый перепад температур, то может ли быть различной плотность
(интенсивность) теплового потока через эти стенки?
8.Если у однородной цилиндрической стенки исследовать два одинаковых по
толщине слоя — внутренний и внешний, то могут ли перепады температур в этих
слоях оказаться одинаковыми?
2.17. Теплопроводность при нестационарном тепловом режиме
Методы решения задач теплопроводности в нестационарном режиме.
Теплопроводность тонкой пластины, длинного цилиндра при граничных условиях третьего рода. Анализ решений. Частные случаи.
Нагревание (охлаждение) параллелепипеда и цилиндра конечной длины.
Определение количества теплоты, отдаваемой или воспринимаемой телом в
процессе нестационарной теплопроводности. Регулярный тепловой режим
нагревания (охлаждения) тел. Численный метод решения задач нестационарной
теплопроводности. Использование ЭВМ.
Литература: [4, гл. 3, § 3.1-3.6. 3.8-3.11].
32
Методические указания
При выводе расчетных формул следует особо отметить момент появления
безразмерных комплексов, названных числами Био (Bi), Фурье (Fo),
безразмерной температуры θ и безразмерной линейной координаты (X или R),
уяснить в дальнейшем их решающую роль в расчетах нестационарных
процессов теплопроводности (более подробно понятия о числах подобия
рассматриваются в теме 18). Студент должен уметь пользоваться графиками
зависимости между числами Фурье, Био и безразмерной температурой, выбирать необходимый график в зависимости от условия задачи, предусматривающего вычисление безразмерной температуры на поверхности или в середине
тела (пластины, цилиндра). Следует знать особенности процессов нестационарной теплопроводности в некоторых характерных частных случаях,
когда число Био стремится к нулю или бесконечности, или число Fo >0,3, что
упрощает расчетные формулы.
При изучении способа определения количества теплоты, выделяемой
(поглощаемой) телом в процессе нестационарной теплопроводности, надо
усвоить понятие о средней безразмерной температуре тела, уметь ее определять
и использовать для расчета количества теплоты, в частности, при Fo>0,3.
Вопросы для самопроверки
1.Достаточно ли знать дифференциальное уравнение теплопроводности,
чтобы
определить
температурное
поле
в
твердом
теле
(в любой точке и в любой момент времени)?
2.Одинаковы ли единицы измерения коэффициента температуропроводности и
кинематической вязкости?
3.Всегда ли начальное условие выражается в виде to=const?
4.Верно ли, что безразмерная координата X становится равной нулю в
центре пластины толщиной 2δ?
5.Включен ли в число Био коэффициент теплопроводности жидкой среды
(окружающей жидкости)?
6.Одинаково ли написание линейных размеров, входящих в число Фурье для
пластины и для цилиндра?
33
7.Может ли безразмерная температура увеличиваться в режиме нагревания и в
режиме охлаждения?
8.Достаточно ли одной из диаграмм вида θ=f (Fo Bi) для неограниченной
пластины, чтобы определить разность безразмерных температур между
серединой и поверхностью ее?
2.18. Основные положения конвективного теплообмена
Теплоотдача в однофазных жидкостях при фазовых и химических превращениях, при вынужденной и естественной конвекции. Физические свойства
жидкости, существенные для процессов течения и теплоотдачи.
Особенности теплообмена при ламинарном и турбулентном течениях
жидкости. Гидродинамический и тепловой пограничные слои. Основные допущения теории пограничного слоя. Система дифференциальных уравнений
конвективного теплообмена; условия однозначности.
Литература: [4, гл. 4].
Методические указания
Необходимо знать классификацию явлений конвективного теплообмена,
научиться определять коэффициент теплоотдачи в наиболее характерных
случаях конвективного теплообмена, обратить внимание на решающую роль
гидродинамического и теплового пограничных слоев и ясно представлять
различие в этих понятиях. При изучении § 4.5 [4], как и в дальнейшем, следует
ясно представлять расположение системы координат X - Y относительно
поверхности теплообмена.
Разложение локальных значений скорости и температуры в турбулентном
потоке на среднюю и пульсационную составляющие позволяет обобщить
полученные ранее дифференциальные уравнения конвективного теплообмена
на случай турбулентного
течения
(см. уравнения (4.44)...(4.46)
Необходимо понять физический смысл величин qT и
SТ
[4]).
как интенсивностей
переноса теплоты и количества движения в поперечном сечении пограничного
слоя (через единицу поверхности АА на рис. 4.10 [4]). Следует освоить понятия
λт μт Єq и степени турбулентности Тu , используемые в последующих частях
курса.
34
Вопросы для самопроверки
1.Можно ли коэффициент теплопроводности λ. и коэффициент теплоотдачи
α выразить в одинаковых единицах?
2.Могут ли быть одинаковыми единицы коэффициентов вязкости динамического и кинематического?
3.Можно ли определить коэффициент объемного расширения газов и
жидкости по формуле β=1/Т?
4.Может ли свободная конвекция влиять на теплоотдачу в условиях
вынужденной конвекции?
5.Могут ли совпадать по толщине
гидродинамический и тепловой
слои?
6.Может ли кинематический коэффициент вязкости воды на линии
насыщения
в
интервале
температур 30...90°С достигнуть значения
υ = 0,4 - 10 6 м2/c?
7.Верно ли, что коэффициент температуропроводности у воды на линии
насыщения при температуре +20°С больше, чем у сухого воздуха при
атмосферном давлении и температуре –50°С?
2.19. Основы метода подобия и моделирования
π - теорема. Приведение уравнений конвективного теплообмена к
безразмерному виду. Числа подобия. Общие условия подобия физических процессов. Свойства подобных процессов. Сущность моделирования.
Литература: [4, гл. 5].
Методические указания
Полезно обратить внимание на то, что в безразмерные величины (Gr,
Eu, θ и др.) входят не температуры и давления, а разности температур или
давлений. Следует различать: а) определение подобия как описание всех
признаков подобия и б) условие подобия как описание минимума признаков,
достаточных для выполнения всех остальных признаков подобия. Определением
подобия является формула (5-26) [41, согласно которой, если процессы подобны,
то подобны формы их границ (геометрическое подобие), поля скоростей и
давлений (гидродинамическое подобие), поля температур и плотностей
35
тепловых потоков (тепловое подобие). Условием подобия является теорема
Кирпичева - Гухмана [4, § 5.4, п.п. 1, 2, 3]'.
Ограничения, накладываемые на произвольный выбор констант подобия
[4, § 5.6], следует рассматривать как важнейшие следствия физического
подобия.
Вопросы для самопроверки
1.Совпадают ли по форме безразмерные комплексы, выражающие число Био
и число Нуссельта?
2.Совпадают ли по содержанию безразмерные комплексы, выражающие
число Био и число Нуссельта?
3.Содержится ли одноименная физическая величина
в каждом из
комплексов, выражающих числа Нуссельта, Пекле, Рейнольдса и Грасгофа?
4.Является ли необходимым условием подобия процессов конвективного
теплообмена равенство числовых значений, характеризующих условия
однозначности?
5.В ряду безразмерных величин - Θ, W, Eu, Re, Nu, Pr, Gr, Pe содержатся ли
независимые переменные?
6.Содержатся ли в этом ряду зависимые переменные?
7.В том случае, когда подобие двух процессов достигнуто, могут ли
отличаться числовые значения физических величин в сходственных точках?
8.В том случае, когда подобие двух процессов достигнуто, равны ли в
сходственных точках одноименные зависимые безразмерные величины?
2.20. Общие вопросы расчета конвективной теплоотдачи
Осреднение
коэффициентов
теплоотдачи.
Осреднение
температуры
жидкости по сечению и длине канала. Осреднение температурного напора по
длине канала. Выбор определяющих размеров и температур.
Обобщение опытных данных. Получение эмпирических уравнений.
Литература: [4, § 6.1, 6.2, 6.6].
36
Методические указания
В связи с неопределенностью формулы Ньютона - Рихмана в отношении того,
что принимать за tЖ , возникает необходимость в дополнительном указании,
какой из возможных вариантов задания определяющей температуры выбран в
каждом конкретном исследовании и использован для построения расчетного
уравнения. В зависимости от названия определяющей температуры изменяется
вид расчетного уравнения и его точность.
Вопросы для самопроверки
1. Верно ли, что зависимость коэффициента теплоотдачи α от температуры
представлена в таблицах теплофизических свойств веществ наряду с λ, α и
другими величинами?
2. Может ли среднелогарифмический температурный напор превышать все
местные температурные напоры на участке осреднения?
3. Верно ли, что в качестве определяющего размера может быть взят
любой линейный размер, введенный в состав условий однозначности?
4. Верно ли, что в качестве определяющей температуры может быть
взята любая температура, введенная в условия однозначности?
5. Можно ли по среднему температурному напору вычислить начальный Δt1 и
конечный Δt2 температурные напоры?
6. Можно ли по начальному Δt1 и конечному Δt2 температурным напорам
вычислить средний температурный напор Δ
2.21. Теплоотдача при вынужденном продольном
омывании плоской поверхности
Характер вынужденного неизотермического течения и теплообмена на
плоской поверхности. Теплоотдача при ламинарном течении в пограничном
слое; метод теоретического расчета; расчетные уравнения, полученные
опытным путем. Теплоотдача при турбулентном течении в пограничном слое.
Уравнения неразрывности, движения и энергии для турбулентных потоков;
коэффициенты турбулентного переноса количества движения и теплоты; метод
полуэмпирического расчета; расчетные уравнения, полученные опытным путем.
Литература: [4, гл. 7].
37
Методические указания
Выбор плоской поверхности теплообмена в качестве первого объекта для
изучения процесса теплообмена обусловлен тем, что аналитическое описание
явлений в пограничном слое вблизи плоской поверхности более простое, чем
вблизи поверхностей криволинейной формы. В частности, при ламинарном
течении удается определить соотношение между толщинами теплового и
гидродинамических слоев, зависящие только от числа Рr, формула (7.8.) [4], а
также построить без помощи опытов безразмерное уравнение теплообмена
(7.11) [4], включая и числовые коэффициенты уравнения.
Необходимо отметить роль множителя (Рrж/Рrс)0,25 , учитывающего переменность физических свойств жидкости в пограничном слое, а также теплового режима стенки, характеризуемого постоянством по длине температуры
или интенсивности теплообмена.
Вопросы для самопроверки
1. Зависит ли отношение толщин теплового и гидродинамического пограничного слоев при ламинарном движении от физических свойств жидкости?
2. Верно ли, что оба зависимых числа подобия - Nux,
и Nu -
увеличиваются по мере удаления от передней кромки пластины?
3. Может ли поправочный множитель (Рrж/Рrс)0,25 учитывающий изменение
температуры по толщине пограничного слоя, зависеть от значения и
направления теплового потока через слой?
4. Зависит ли толщина вязкого подслоя при турбулентном течении от
кинематического коэффициента вязкости?
5. Верно ли, что Nuжх при турбулентном течении вдоль пластины увеличивается с увеличением скорости обтекания?
6. Являются ли коэффициенты теплоотдачи, вычисляемые по эмпирической
формуле
(7.39)
[4],
средними
значениями
коэффициента
теплоотдачи
по длине пластины?
38
2.22. Теплоотдача при вынужденном движении жидкости в трубах и при
поперечном смывании труб и пучков труб
Особенности течения и теплообмена в трубах. Участки гидродинамической
и тепловой стабилизации. Стабилизированное течение. Теплоотдача при
ламинарном и турбулентном режимах течения жидкости в трубах. Теплоотдача
при вынужденном поперечном омывании труб и пучков труб; расчетные
уравнения. Современные методы расчета теплообмена с использованием ЭВМ.
Расчетные уравнения, полученные опытным путем.
Литература: [4, гл. 8 и 9].
Методические указания
Рассматриваются три вида вынужденного движения жидкости: внутри
трубы, поперек трубы и поперек пучка труб. В каждом из видов изучается
ламинарный и турбулентный режимы течения. Кроме того, при ламинарном
режиме течения различают две его разновидности - вязкостный и вязкостногравитационный режимы. При анализе всех видов течения следует различать
теплообмен в пределах начального теплового участка и теплообмен стабилизированный, а также местные и средние значения коэффициента теплоотдачи.
Вопросы для самопроверки
1. Одинаковы ли значения местного и среднего коэффициентов тепло
отдачи на участке термической стабилизации?
2. Могут ли отличаться значения местного и среднего коэффициентов
теплоотдачи за пределами участка термической стабилизации?
3. Применима ли
известная расчетная формула
Nu ж, d=0,021·Reж, d0,8-Рrж 0,43(Рrж/ Рrс)0,25 только для турбулентного режима течения?
4. Одинаковы ли наименования чисел подобия, включенных в формулы для
вязкостного и вязкостно-гравитационного режимов течения?
5. Допускается ли применение расчетных формул, соответствующих
течению в круглых трубах, для расчета теплоотдачи при течении в трубах
некруглого поперечного сечения?
6. Одинаковы ли местные коэффициенты теплоотдачи по окружности
трубы при поперечном ее омывании жидкостью?
39
7. Возможен ли при турбулентном течении коэффициент теплоотдачи
у шероховатой трубы меньший, чем у гладкой трубы?
2.23. Теплоотдача при свободном движении жидкости
Теплоотдача при свободном движении жидкости вдоль вертикальной
стенки, вблизи горизонтальных труб и пластин. Анализ задачи о конвективном
теплообмене при свободном движении жидкости методом подобия. Расчетные
уравнения теплоотдачи .Свободно - конвективный теплообмен в ограниченном
пространстве.
Литература: [4, гл. 10].
Методические указания
Необходимо освоить классификацию процессов теплоотдачи при свободном
движении жидкости, уметь осуществлять выбор безразмерных уравнений,
позволяющих рассчитать коэффициент теплоотдачи для каждого частного
случая.
Вопросы для самопроверки
1. Подобны ли распределения температуры и скорости по толщине по
граничного слоя при свободном ламинарном движении жидкости вдоль
вертикальной пластины в неограниченном объеме?
2. Верно ли, что при свободной конвекции вдоль вертикальной пластины
в неограниченном объеме в случае ламинарного режима коэффициент
теплоотдачи, средний на участке высотой х, больше, чем коэффициент
теплоотдачи местный на высоте х?
3. Можно ли моделировать условие t^const при свободной конвекции
на вертикальной стенке, используя внешнюю поверхность вертикальной
трубы, обогреваемой изнутри насыщенным паром?
4. Можно ли моделировать условие tс=const при свободной конвекции
на вертикальной стенке, используя внешнюю поверхность вертикальной трубы,
обогревая ее пропусканием через нее электрического тока?
5. Возможна ли свободная конвекция вдоль вертикальной стенки без
участка с ламинарным движением?
6. Возможна ли свободная конвекция вдоль вертикальной стенки без
40
участка с турбулентным движением?
7. Зависит ли местный коэффициент теплоотдачи, при турбулентном
движении возле вертикальной стенки в неограниченном объеме от высоты
участка?
8. Можно ли исключить свободную конвекцию в зазоре между двумя
горизонтальными поверхностями, отличающимися друг от друга температурой?
2.24. Отдельные задачи конвективного теплообмена в однородной среде
Теплообмен при течении жидкометаллических теплоносителей. Теплообмен
при наличии в жидкости внутренних источников теплоты.
Литература: В [4] глава 11 §11.1 - до пояснений к рис. 11.1 включительно,
и § 11.3 - до пояснений к рис. 11.6 включительно.
Методические указания
Изучению подлежат две темы: теплоотдача жидких металлов и теплоотдача
при течении газа с большой скоростью.
При освоении первой темы следует выделить преимущества жидких металлов перед газами или водой в качестве теплоносителей, а также специфичность их теплофизических свойств (низкое значение числа Рr), и, как
следствие, особенность температурных полей (существенное утолщение теплового пограничного слоя). Следует обратить внимание на значение контактного
термического сопротивления, ухудшающего процесс теплоотдачи по сравнению
с данными, предсказываемыми теорией.
При освоении второй темы - теплопередачи при течении газа с большой
скоростью - нужно уяснить новые понятия, такие, как температура адиабатического торможения Т0 и адиабатическая температура стенки Тас. имея в виду
при этом, что последняя изменяется от Тr до Т0 в зависимости от условий
торможения, определяемых коэффициентом восстановления температуры г.
Если Т0 легко вычислить теоретически (например, по формуле (11.15 [4]), то
для определения Тr нужно знать еще и величину r.
41
Вопросы для самопроверки
1.Верно ли, что число Прандтля жидких металлов существенно ниже,
чем газов и воды?
2.Является ли процесс торможения газа в струе изобарным?
3.Может ли процесс торможения газа в струе быть адиабатным?
4.Всегда
ли
повышается
температура
газа
в
струе
на
участке
адиабатного торможения?
5.Верно
ли,
что
энтальпия
одного
кг
газа
и
одного
кг
воды,
движущихся с одинаковой скоростью, повышается одинаково после полного
адиабатического торможения?
6.Верно ли, что температура газа и воды, движущихся с одинаковой
скоростью, повышается одинаково после полного адиабатического
торможения?
7.Возрастает ли температура торможения газа при увеличении числа
Маха?
8.Может ли адиабатная температура Та.с (например, термометра)
превышать температуру адиабатного торможения Тo?
2.25. Теплообмен при конденсации чистого парa
Пленочная и капельная конденсации. Конденсация пара на вертикальных
стенках. Теплоотдача при ламинарном течении пленки. Метод теоретического
расчета. Влияние различных факторов на теплоотдачу. Теплоотдача при
смешанном режиме стекания пленки конденсата; метод расчета; расчетные
уравнения для теплоотдачи. Конденсация пара на горизонтальных трубах и
пучках труб. Характер обтекания конденсатом пучков труб, изменение
теплоотдачи по рядам, влияние скорости пара и других факторов. Расчет теплоотдачи при конденсации пара на горизонтальных пучках труб. Теплоотдача
при капельной конденсации пара.
Литература: [4, гл. 12, § 12.1-12.4].
42
Методические указания
Следует представлять себе следующую классификацию процессов: в
объеме или на поверхности, пленочную или капельную, при неподвижном или
движущемся паре, при паре насыщенном, влажном или перегретом. В случае
пленочной конденсации различают режимы стекания пленки: ламинарный и
смешанный, т.е. ламинарный, сосуществующий с турбулентным. В случае
капельной
конденсации
различают
режимы
с
малым
и
большим
температурными напорами. Следует различать две составляющие термического
сопротивления тепловому потоку при конденсации - сопротивление пленки
конденсата на поверхности стенки и термическое сопротивление на границе раздела фаз (в кнудсеновском слое). Последнее определяется коэффициентом конденсации К и проявляется при малых давлениях (р<104 Па), см. рис. 12.3 [4].
При изучении темы следует обратить внимание на интерпретации числа Re
для пленки конденсата согласно формуле (12.8) [4], на различие в определяющих размерах чисел Рейнольдса для пленки и для пара [4, § 12.4], на то
существенное обстоятельство, что число Рейнольдса пленки становится зависимым, т.е. определяемым числом подобия, содержащим в себе искомую величину - коэффициент теплоотдачи a, а также на определяющие независимые
числа подобия - Z, Ga, Ar. Изучение подтем пленочного и капельного видов
конденсации следует завершить анализом диаграмм [4, рис. 12.8 и 12.14],
удобных для многих практических расчетов.
Вопросы для самопроверки
1. Верно
ли,
что
для
критического
числа
Рейнольдса
Reкр≈400,
характеризующего при конденсации пара переход от ламинарного режима
стекания пленки к турбулентному, определяющим размером служит высота х
участка стекающей пленки?
2. Входит ли в число Рейнольдса для пленки конденсата коэффициент
теплоотдачи при конденсации?
3. Зависит ли коэффициент теплоотдачи при ламинарном режиме
конденсации от температурного напора?
4. Может ли средний коэффициент теплоотдачи при пленочной
43
конденсации неподвижного пара на вертикальной поверхности уменьшаться
при увеличении температурного напора?
5. Верно ли, что коэффициент теплоотдачи при капельной
конденсации водяного пара больше, чем при пленочной конденсации?
6. При конденсации пара на вертикальных стенках толщина пленки
конденсата увеличивается по мере стекания ее вниз. Может ли при этом
7. возрастать коэффициент теплоотдачи (средний или местный)?
2.26. Теплообмен при кипении однокомпонентных жидкостей
Механизм переноса теплоты при кипении. Влияние смачиваемости стенки
жидкостью, краевой угол. Рост, отрыв и движение пузырей пара. Минимальный
радиус пузыря; число действующих центров парообразования. Режимы кипения
жидкости в большом объеме. Первая и вторая критические плотности теплового
потока. Расчет критических тепловых нагрузок. Зависимость коэффициента
теплоотдачи от давления, физических свойств жидкости, состояния поверхности
и других факторов при кипении в большом объеме.
Теплообмен при кипении жидкости в трубах; зависимость коэффициента
теплоотдачи от скорости циркуляции, плотности теплового потока и других
факторов. Расчет теплоотдачи в трубах.
Литература: [4, гл. 13, § 13.1-13.5, 13.9, 13.10].
Методические указания
Изучите классификацию процессов кипения, а для каждого элемента этой
сложной классификации - методику определения коэффициентов теплоотдачи,
плотности теплового потока или температуры стенки, иногда температуры
перегрева жидкости.
Заинтересованность
в
высокой
интенсивности
теплообмена
заставляет
обратить особое внимание на пузырьковый режим кипения. Однако именно для
этой области кипения пока не существует строгой теории, а имеются лишь
отдельные
приближенные
решения,
которые
отличаются
различными
подходами к процессу кипения. Поэтому, при кипении различных жидкостей в
неограниченном объеме, рекомендуется пользоваться формулой
44
Г.Н. Кружилина
Nu
где

Nu
c Re Pr ,
w
vж
Re
;
1
3
ж
n
ж
(2.15)
q
w
r
,
- м/с- приведенная
n
скорость
ж
парообразования, 
паровой
r
фазы,
с рж Т s
2
,Vж ,
поверхностного
м - характерный линейный размер
,
п
ж
, с рж , Рrж ,
натяжения,
ж
, ,-
соответственно
кинематическая
вязкость,
коэффициент
коэффициент
теплопроводности, удельная теплоемкость, число Прандтля, плотность жидкости при температуре насыщения ts,
п
- плотность пара при ts, q, Вт/м2 -
плотность теплового потока, подводимого к поверхности нагрева, Ts - температура насыщения
Значения с и п принимаются:
при Re* < 0,01
с = 0,0625,
п = 0,5 ;
при Re* > 0,01
с = 0,125,
n= 0,65.
Определив коэффициент теплоотдачи
по этой формуле для заданного
значения теплового потока q, Вт/м2 , получают возможность вычислить и
температурный напор.
tc-tн=q/a
Более простая формула теплоотдачи при пузырьковом кипении, но применимая только для воды, рекомендована Михеевым М.А. С учетом последующего уточнения (см.: Рассохин Н.Г., Швецов Р.С., Кузьмин А.В. Расчет
теплоотдачи при кипении. Теплоэнергетика, 1970, № 9, с. 58-59) она имеет
вид:
при 0,1 Мпа ≤ р ≤ЗМПа, a = 6,0p1/5 ·q2/3;
при 3 МПа
где
р
20МПа,
= 3,33p3/4·q2/3,
- Вт/(м2·К), р - МПа, q - Вт/м2.
45
Вопросы для самопроверки
1.Верно ли, что увеличение критического радиуса парового пузырька
способствует увеличению коэффициента теплоотдачи?
2.Верно ли, что для пузырькового режима кипения максимальные
температурные напоры (Тс – Тн) ниже, чем для пленочного режима?
3.Верно ли, что с увеличением теплопроводности кипящей жидкости
коэффициент теплоотдачи увеличивается, а с увеличением вязкости
уменьшается?
4.Согласны ли Вы с утверждением, что в промышленных
теплообменниках с кипением теплоносителя режим кипения пленочный?
5.Одинаковы ли процессы перехода от пузырькового к пленочному
режиму кипения в случаях регулируемой температуры стенки и регулируемой
плотности теплового потока?
6.Можно ли приведенную скорость парообразования выражать в
метрах в секунду (м/с)?
2.27. Конвективный тепло- и массообмен
Основные положения теории массообмена. Термо- и бародиффузия. Закон
Фика. Коэффициент диффузии, факторы, влияющие на коэффициент диффузии.
Конвективный массообмен как совокупность молярного и молекулярного
переноса вещества. Плотность потока массы в процессе конвективного
массообмена. Диффузионный пограничный слой. Система дифференциальных
уравнений
диффузионного
пограничного
слоя. Граничные условия на
поверхности раздела фаз. Коэффициент массоотдачи. Применение методов
подобия и размерностей к процессам массообмена. Диффузионное число
Нуссельта, диффузионное число Прандтля. Аналогия процессов тепло- и
массообмена. Перенос загрязняющих примесей в атмосфере. Значение охраны
окружающей среды в современных условиях.
Литература: [4, гл. 14].
46
Методические указания
Процесс диффузии сопровождается двумя явлениями - переносом массы и
переносом энергии. Различают диффузию в газообразных, жидких и твердых
телах, в двухкомпонентных (бинарных) средах и многокомпонентных средах,
массоотдачу через полупроницаемую и полностью проницаемую поверхности,
концентрационную диффузию, термо- и бародиффузию. При этом на
диффузионный перенос массы часто накладывается также конвективный
перенос.
При изучении темы следует отметить формальную аналогию процессов
теплопроводности, конвекции и концентрационной диффузии; подобие законов
Фурье, Ньютона и Фика, соответственно уравнений энергии, движения и
массообмена, подобие полей температуры, скорости и концентрации в пограничном слое, подобие явлений теплоотдачи, трения и массоотдачи.
Необходимо обратить внимание и на особенности диффузионных процессов - появление диффузионного термоэффекта, разнообразие выражений и
даже единиц для коэффициентов молекулярной диффузии D и Dp, а также
коэффициентов массоотдачи
и
Р.
Вопросы для самопроверки
1. Одинаковы ли единицы измерения коэффициента молекулярной
диффузии и кинематического коэффициента вязкости?
2. Одинаковы ли единицы измерения коэффициента теплоотдачи
коэффициента массоотдачи
и
?
3. Содержится ли коэффициент теплоотдачи
в диффузионном числе
Нуссельта?
4. Содержится ли коэффициент теплопроводности в диффузионном
числе Нуссельта?
5. Может ли процесс испарения в парогазовую смесь усилить
теплообмен между жидкостью и парогазовой смесью?
6. Может ли процесс испарения в парогазовую смесь увеличить
коэффициент конвективной теплоотдачи над поверхностью жидкости?
47
2.28. Основные законы теплового излучения
Основные понятия и законы. Природа теплового излучения. Лучистый
поток.
Плотность
лучистого
потока.
Интенсивность
излучения.
Поглощательная, отражательная и пропускательная способность тел.
Законы излучения абсолютно черного тела: закон Планка, закон Вина. Серое
тело. Закон Стефана- Больцмана. Степень черноты. Закон Кирхгофа для
монохроматического
и
интегрального
излучения.
Закон
Ламберта.
Особенности теплообмена излучением в поглощающих средах, теплообмена
излучением
между
излучающими
газом
или
паром
и
теплообменной
поверхностью.
Литература: [4, гл. 16].
Методические указания
Излучение реальных тел следует рассматривать как приближение к равновесному, описываемому формулами Планка, Вина и Стефана - Больцмана,
которые отличаются от соответствующих одноименных законов черного излучения только опытными коэффициентами, называемыми спектральной
степенью черноты или степенью черноты (интегральной), причем для серых тел
спектральные степени черноты одинаковы при всех длинах волн и равны
интегральной степени черноты. Следует четко представлять себе закон
Кирхгофа, с помощью которого устанавливается связь между поглощательной и
излучательной способностью (степенью черноты) тел.
Вопросы для самопроверки
1. Может ли тело поглощать больше лучистой энергии, чем излучать?
2. Может ли отраженный лучистый поток быть больше падающего
лучистого потока?
3. Всегда ли тело, температура которого выше окружающей среды,
излучает энергии больше, чем поглощает?
4. Может ли возрастать спектральная плотность потока излучения при
увеличении длины волны излучения?
5. Может ли собственное излучение тела быть меньше отраженного
этим телом излучения?
48
6. Может ли собственное излучение тела быть больше поглощенного
этим телом излучения?
7. Может ли собственное излучение тела быть больше эффективного
излучения этого тела?
2.29. Теплообмен излучением между телами, разделенными
прозрачной средой
Виды лучистых потоков. Их взаимная связь. Интегральные уравнения
излучения. Угловые коэффициенты и взаимные поверхности. Расчет теплообмена излучением в системе двух тел. Расчет теплообмена излучением в
замкнутой системе, состоящей из серых тел. Особенности излучения газов и
паров.
Литература: В [4] гл. 17 § 17.1 - 17.6,17.8, 17.14.1; исключить пункты 17.3.117.3.3 в §17.3; гл. 18, §18.1, 18.2.
Методические указания
При изучении теплообмена излучением между телами, произвольно расположенными в пространстве, выделите понятия элементарных и средних
угловых коэффициентов. Необходимо иметь представление о роли приведенной
поглощательной способности, уметь определять ее в простейших случаях.
Вопросы для самопроверки
1. Существует ли результирующий лучистый поток в зазоре между
двумя параллельными стенками, если поверхности стенок имеют
одинаковую температуру?
2. Может ли серое тело излучать больше энергии, чем черное тело
таких же размеров и в такой же окружающей среде, если температуры и серого
и черного тел одинаковы?
3. Может ли серое тело поглощать больше энергии, чем черное тело
таких же размеров и в такой же окружающей среде, если температуры серого
и черного тел одинаковы?
4. Может ли серое тело поглощать больше энергии, чем черное тело,
если размеры и температуры серого и черного тел одинаковы, а температура
окружающих тел различна?
49
5. Можно ли определить результирующий поток излучения как
разность собственного и падающего излучения?
6. Влияет ли форма и расположение излучающих тел на способ расчета
приведенной поглощательной способности?
7. Влияет ли температура излучающих тел на способ расчета
приведенной поглощательной способности?
2.30. Теплообменные аппараты
Общие сведения. Назначение теплообменников. Их классификация по
принципам действия. Основы теплового и гидравлического расчета теплообменников. Уравнение теплового баланса и уравнение теплопередачи.
Средний температурный напор. Определение среднего температурного
напора для основных схем движения теплоносителей. Выражение для полного
падения давления в теплообменнике. Сопротивление трения и местные
сопротивления. Затраты напора, обусловленные ускорением потока и преодолением гидростатического давления столба жидкости. Мощность, необходимая для перемещения теплоносителей.
Литература: [4, гл. 19, 20].
Методические указания
Основным вопросом темы является анализ уравнения теплового баланса и
уравнения теплопередачи, а также их применение к расчету теплообменников.
Необходимо различать проектный и поверочный расчеты теплообменников,
хорошо разбираться в выводах, относящихся к определению среднего
температурного напора, и овладеть методикой расчета конечных температур.
Вопросы для самопроверки
1. Зависит ли в стационарном режиме количество теплоты, проходя
щей сквозь теплообменную поверхность, от продолжительности режима?
2. Может ли среднелогарифмический температурный напор в прямо точном теплообменнике быть больше, чем каждый из крайних
температурных напоров?
3. Может ли среднелогарифмический температурный напор быть
меньше хотя бы одного из крайних напоров?
50
4. Верно ли, что включение теплообменника по схеме прямотока не
может увеличить средний логарифмический напор по сравнению со схемой
противотока?
5. Можно ли вычислить среднюю по сечению скорость струи, зная
только ее объемный расход через сечение и площадь сечения?
6. Верно ли, что при 20°С и нормальном давлении кинематический
коэффициент вязкости у воздуха больше, чем у воды?
7. Растет ли сопротивление трения при увеличении скорости потока в
теплообменнике?
3. СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
3.1. Общие методические указания
На практических занятиях решаются задачи по основным разделам курса.
Наибольшее внимание уделяется усвоению законов термодинамики и тепломассообмена, методам расчета с использованием таблиц, диаграмм и
другого справочного материала и методам термодинамического анализа процессов и циклов энергетических установок.
На практических занятиях каждый студент работает самостоятельно,
выполняя индивидуальные расчеты согласно своего варианта.
В ходе выполнения лабораторных работ студенты получают практические
навыки по работе с приборами и установками, по измерениям электрических и
тепловых характеристик, по обработке экспериментальных данных в том числе
с применением ЭВМ
По каждой работе составляется отчет с указанием цели работы, приводится
схема установки и ее описание, таблицы измерений, расчет и обработка
результатов опыта, вывод.
3.2. Тематика практических занятий
1 . Расчет термических и калорических параметров идеального газа.
2. Расчет процессов идеального газа.
3. Расчет параметров воды и водяного пара.
4. Расчет процессов воды и водяного пара.
5. Расчет истечения газов и паров. Дросселирование.
51
6. Процессы компрессоров.
7. Расчет циклов газовых двигателей (ГТД и ГТУ, ДВС).
8. Расчет циклов паротурбинных установок.
9. Расчет циклов холодильных машин.
10.Расчет стационарной теплопроводности.
11 . Расчет теплопередачи, в том числе со сложным теплообменом.
12.Теплопередача оребренных поверхностей.
13.Расчет теплоотдачи при свободной и вынужденной конвекции.
14.Расчет теплообмена при конденсации и кипении.
15.Расчет теплообмена излучением в диатермичной и поглощающей
среде.
16. Расчет теплообменных аппаратов.
3.3. Перечень лабораторных работ
1. Определение изобарной теплоемкости воздуха .
2. Оценка необратимости течения воздуха.
3. Изохорное нагревание воды и водяного пара.
4. Определение абсолютной и относительной влажности воздуха.
5. Исследование процессов во влажном воздухе.
6. Исследование обратимых циклов паротурбинной установки на ЭВМ.
7. Экспериментальное определение коэффициента теплопроводности
стационарными методами (метод шара, пластины и цилиндра).
8. Экспериментальное определение коэффициента теплопроводности и
температуропроводности методом регулярного режима.
9. Исследование зависимости коэффициента теплоотдачи при
свободной конвекции от формы, размеров и ориентации поверхности в
пространстве.
10.Экспериментальное определение уравнения подобия при
вынужденном течении вдоль плоской поверхности.
11.Исследование зависимости интегрального коэффициента излучения
от температуры радиационным методом.
52
4. КОНТРОЛЬНЫЕ РАБОТЫ (6 часов)
4.1. Общие методические указания
По дисциплине предусмотрено выполнение трех контрольных работ. Первая
и вторая контрольные работы содержат по 4 задания и по 48 контрольных
вопросов, третья контрольная работа - 5 заданий и 48 контрольных вопросов.
Одно задание содержит либо одну задачу, рассчитанную на 25 вариантов,
либо 5 задач, каждая из которых рассчитана на 5 вариантов.
Кроме того, вторая и третья контрольные работы содержат задания, помеченные одной или двумя звездочками (* **). Задачи этих заданий не являются обязательными, но рекомендуются для решения с целью повышения
уровня подготовки по данной дисциплине. Теоретические основы и рекомендации, необходимые для решения этих задач, так же как и обязательных,
приведены в учебном пособии [7]. Решение этих дополнительных задач повышает рейтинг студента и учитывается экзаменационной оценкой.
В каждом задании контрольной работы студент должен решить одну
обязательную задачу, согласно своего варианта и ответить на 4 контрольных
вопроса.
Номера вариантов и номера вопросов даны в табл.1 в зависимости от двух
последних цифр шифра студента. Например, при шифре 6370/21 (последние две
цифры - 21) студент в каждой контрольной работе решает 21 вариант и
отвечает на контрольные вопросы: 4, 19, 33, 37.
53
Таблица 1
№
№
№№
шифра вар.
вопросов
студ. задачи
01
1 13 25 37
1
03
2 14 26 38
2
02
3 15 27 39
3
04
4 16 28 40
4
05
5 17 29 41
5
06
6 18 30 42
6
07
7 19 31 43
7
08
8 20 32 44
8
09
9 21 33 45
9
10
10 22 34 46
10
11
11 23 35 47
11
12
12 24 36 48
12
13
7 23 25 45
13
14
8 24 26 44
14
15
9 13 27 43
15
16
10 14 28 42
16
17
11 15 29 41
17
18
12 16 30 40
18
19
6 17 31 39
19
20
5 18 32 38
20
21
4 19 33 37
21
22
3 20 34 46
22
23
2 21 35 47
23
24
1 22 36 48
24
25
1 16 32 40
25
26
2 17 31 39
1
27
3 18 30 38
2
28
4 19 29 37
3
29
5 20 28 41
4
30
6 21 27 42
5
31
32
33
34
35
6
7
8
9
10
7
8
9
10
11
22
23
24
15
14
26
25
33
34
35
43
44
45
46
47
№
шифра
студ.
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
№
вар.
задачи
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12
4
3
2
1
5
6
7
8
12
11
10
9
12
11
10
9
8
7
6
5
4
3
2
1
2
4
6
8
10
13
13
14
15
16
17
18
19
20
21
22
23
24
19
18
17
16
15
14
13
20
21
22
23
24
13
14
15
166
17
36
25
27
29
31
33
35
36
34
32
30
28
26
25
26
27
28
29
30
31
32
33
34
35
36
29
30
31
32
33
48
43
42
41
37
38
39
40
44
45
46
47
48
48
47
46
45
44
43
42
41
40
39
38
37
40
39
38
37
42
66
67
68
69
70
16
17
18
19
20
12
11
9
7
5
18
19
20
21
22
34
35
36
25
26
41
43
44
45
46
N°№ вопросов
54
Для изучения дисциплины и решения контрольных работ надо обязательно иметь два учебника [1, 4] и таблицы воды и водяного пара [3]. Остальные справочные материалы, необходимые для решения задач, можно
найти в ПРИЛОЖЕНИЯХ к учебникам и учебному пособию [7].
Перед решением контрольной работы следует внимательно ознакомиться
с материалом учебного пособия [7] к данной работе, где содержится краткая
теория (необходимые понятия и формулы), примеры расчета, рекомендации
к решению задач, ссылки на материал в учебнике, затем познакомиться с
данной темой по учебнику. После этого можно приступать к решению задач и
ответам на контрольные вопросы. При этом необходимо выполнять
следующие требования:
1.Приводить полностью условие задачи с исходными данными.
2.Решение задачи сопровождать кратким пояснительным текстом, в
котором указывать, какая величина определяется
и по какой формуле,
какие величины подставляются в формулы и откуда они берутся (из условия
задачи, из справочника или были определены выше и т.д.).
3.Вычисления производить в единицах СИ, анализировать размерность
величин, в формулы подставлять численные значения всех величин, после
этого записывать полученный результат, указывать его размерность.
4.После решения задачи выделить ответы, дать краткий анализ
полученных результатов.
5.
Отвечать на контрольные вопросы следует по существу и кратко.
Контрольные работы выполняются в тетради, для заметок рецензента
оставляются поля.
КОНТРОЛЬНАЯ РАБОТА № 1
ЗАДАНИЕ №1 (к.р. № 1)
Расчет параметров и процессов изменения состояния идеального газа
Задача
Для процесса изменения состояния идеального газа 1-2 рассчитать:
• термические параметры р, , Т в начальном и конечном состояниях;
• изменение калорических параметров
u,
h,
s;
55
• теплоту (q) и работу процесса (w, I ).
Исходные данные для расчета приведены в табл. 1 по вариантам.
Для двух-, трех- и многоатомных газов теплоемкость принять постоянной:
для воздуха и азота (N2)
метана (СН4)
сv=20,8 кДж/кмоль·К, для углекислого газа (СО2) и
cv=29,1 кДж/кмоль·К.
Результаты расчета представить в виде табл. 2 и 3. Показать процессы в р-υи T-s- диаграммах.
Таблица 1
№
вар
1
Газ
кг/кмо
ль
воздух 29
2
С02
44
3
Не
4
4
5
СН4
N2
6
Процесс
Параметры
изобарный
р=2бар,
t1=30°C,
t 2=160°C
изохорный
р1=5бар,
υ =0,111 м3/кг, t2=180°C
16
28
политр.
n=1,3
изотерм.
адиабатный
р1=l бар, υ1=1,834м3/кг,
υ1=0,32 м3/кг, р1=3 бар,
воздух
29
изобарный
υ1=0,434 м3/кг, р=2бар, υ2=0,621 м3/кг
7
С02
44
р1= 5бар,
8
Не
4
9
10
СН4
N2
16
28
изохорный
политр.
n=1,75
изотерм.
адиабатный
29
изобарный
11 воздух
12
С02
44
изохорный
13
Не
4
политр. n=0,8
14
СH4
16
изотерм.
15
N2
28
адиабатный
29
изобарный
16 воздух
р1=106ap,
t1=10°C,
t1= 200C,
υ1=0,588 м3/кг,
р2=20бар
р2=18 бар
р2=7,71бар
t1=10°C, υ2=0,314м3/кг
р1=1бар,
t1=50°C,
t=80°C,
p1=3 бар,
р2=20бар
t2=265,9°C
р=2бар, υ2=0,434 м3/кг
t1=160°C,
t1=20 °С,
р 2=30бар
υ =0, 1 1 1 м3/кг, р2=7,7 1 бар
p1=10бар,
t1=10°C,
р2=30бар
υ1=1,834м3/кг, t=80°C, υ2=0,0917м3/кг
υ1=0,32 м3/кг,
υ1=0,434 м3/кг,
t1=50°C,
t2==265,9°C
t1=30°C, t2=160°C
56
Окончание табл. 1
№ Газ
кг/кмол
вар
Процесс
Параметры
17 СО2
ь
44
изохорный
Не
4
политр. n =1,3
19 СН4
16
изотерм.
20
N2
28
адиабатный
υ1=0,62 1 м3/кг, t1=160°C, υ2=0,434 м3/кг
21 воздух
29
изобарный
υ1=0,621 м3/кг, t1=160°C, υ2=0,434 м3/кг
22
С02
44
изохорный
23
Не
4
18
политроп.
24 СН4
16
n =1,75
изотерм.
25
28
адиабат.
N2
p1=7,71 бар,
t1=180°C, t2=20°C
p1,=30бар, υ1=0,253 м3/кг, t2=10°C
p1=20бар,
t1=180 °С,
p2=l бар
t=80°C,
υ =0, 111 м3/кг,
p1=30бар,
t1=180°C,
υ1= 0,09 1 7м3/кг
t2=20 °C
υ2=0,588м3/кг
t = 180 oС,
р2= 1 бар
υ1=0,0889 м3/кг, р2=3 бар
p1=18бар,
Таблица 2
Точки
υ, м3 /кг
р, бар
Т, К
1
2
СP
cv
кДж/кг- К
u
h
кДж/кг
s
кДж/кг · К
Таблица 3
w
q
q кДж/кг
57
ЗАДАНИЕ № 2 (к. р. № 1) Расчет параметров и процессов изменения
состояния водяного пара
Задача
Для процесса изменения состояния водяного пара 1-2 (исходные данные
приведены в табл. 1 по вариантам) рассчитать:
• параметры р,υ, t, u, h, s, x в начальном и конечном состояниях;
• изменение калорических параметров
u, h,
s;
• теплоту (q) и работу(w,) процесса.
Для решения задачи использовать таблицы воды и водяного пара [3].
Результаты расчѐта представить в виде табл. 2 и 3. Процесс показать в р-υ, T-s,
и h-s- диаграммах.
№ вар.
1
Процесс
адиабатный
2
3
4
5
6
7
8
9
10
изохорн
11
ый
12
13
изохорн
14
ый
15
16
17
18
изобарн
19
изотерм
ый
20
ический
21
22
23
24
25
изобарный
изотермический
изохорный
испарение
адиабатный
изобарный
изотермический
изохорный
испарение
адиабатный
изобарный
изотермический
изохорный
конденсация
адиабатный
изобарный
изотермич.
изохорный
конденсация
бар.
адиабатный
изобарный
изотермический
изохорный
испарение
Таблица 1
р1=50 бар,
Дано
t1=440°C,
x2=l
p1=20 бар,
t1=180°C,
p1=0,06 бар,
p1=l бар
p1=5,5 бар,
p1= 20 бар,
t1=180°C,
x1=1,
p1=l бар,
p1=50 бар,
p1=20 бар,
t1=180°C,
p1=0,06 бар,
p1=1
x1=l,
p1=20 бар,
t1=180 oC
p
1=l
oooo…………
p1=l бар,
.p =3 бар,
1
p1=20 бар,
p1=5 бар,
p1=l бар,
t1=99,63°C,
x1=0,8,
x1=0,
υ1=2,733,
x1=0,
x1=l,
x1=l,
x1=l,
p1 =0,6 бар,
x1=0,
h1=3293,2 кДж/к
x1=0,8,
x1=0,
x1=0,115,
x1=l,
t1=155,5°C,
t1=400°C,
x1=l,
t1=320°C,
x1=0,9,
x1=0,961,
t1=400°C,
t1=180°C,
υ1=2,732 M3/KГ,
x1=0,
x2=l
x2=l
x2=l
x2=l
p2=3 бар
t2=400°C
p2= 5 бар
t2=320°C
x2=0,9
р2=3 бар
t2=400°C
p2=5 бар
p2=l бар
x2=0
p2=50 бар
x2=1
x2=0
x2=l
x2=0
p2=50 бар
x2=0,8
x2=0
t2=36,18°C
x2=l
58
Таблица 2
Точки р, бар
υ, м3/кг
t, °C u, кДж/кг h, кДж/кг
s, кДж/кг· К
x
1
2
u
h
кДж/кг
s
кДж/кг·К
q
w
кДж/кг
Таблица 3
ℓ
ЗАДАНИЕ № 3 (к.р. № 1)
Истечение газов и паров из сопел. Дросселирование.
Влажный воздух
Задание № 3 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Из суживающегося сопла вытекает газ, находящийся в резервуаре, давление
и температура в котором постоянны и равны p1, t1. Давление среды, в которую
происходит истечение, рср=30 бар. Скорость на входе в сопло близка к 0. Газ, а
также параметры p1 и t1 даны в табл.1 по вариантам.
Определить скорость истечения газа (с2), температуру газа на выходе из
сопла (Т2 ,К) и расход газа (G,кг/с). если площадь выходного сечения сопла f=20
мм2.
Теплоемкость газа принять постоянной, потерями на трение пренебречь.
Представить процесс истечения газа в р-v и T-s- диаграммах.
59
Таблица 1
№ вар.
1
6
11
16
21
Газ
Гелий
О2
CO2
N2
Воздух
p1, бар
45
90
54,9
70
55
t1,0C
70
40
50
30
80
ч, <~
Задача № 2
Из сопла Лаваля вытекает водяной пар. Давление пара на входе в сопло р1=40
бар, температура (t1) [или степень сухости (x1)] на входе в сопло даны в табл.2
по вариантам. Давление на выходе из сопла р2=1бар. Расход пара G=0,5т/ч.
Потерями на трение пренебречь. Скорость на входе в сопло c1= 0. Принять
Ркр
кр
Р1
0,55.
Определить скорость пара на выходе из сопла (c2) и площадь выходного
сечения (f2, мм2), скорость в минимальном сечении сопла (cкр) и площадь
минимального сечения (fmin , мм2).
При решении задачи воспользоваться таблицами термодинамических
свойств воды и водяного пара [3].
Показать процесс истечения в h-s- диаграмме.
Таблица 2
№ вар.
t1°C
x1
2
450
-
7
400
-
12
350
-
17
300
-
22
1
Задача № 3
Водяной пар с давлением p1=20 бар, и степенью сухости x1 дросселируется
до состояния сухого насыщенного пара (х 2=1). Значения х1 даны в табл.3.
Определить давление пара (р2) и уменьшение температуры при дросселировании (t1-t2), пользуясь таблицами термодинамических свойств воды и
водяного пара [3].
Предоставить процесс дросселирования водяного пара в h-s- диаграмме.
60
Таблица 3
№ вар.
3
8
13
18
23
х1
0,88
0,9
0,92
0,94
0,96
Задача № 4
Влажный воздух с температурой t1 , относительной влажностью (
1
на-
гревается при постоянном давлении р=2бар до температуры t2=80°C. Расход
влажного воздуха G=5кг/с. Значения t1 и
1
даны в табл.4 по вариантам.
Определить подводимую теплоту (Q, кДж/с) и относительную влажность
нагретого воздуха (
2
).
Показать процесс нагрева влажного воздуха в h-d- диаграмме.
Таблица 4
№ варианта
4
9
14
19
24
t1 0C
0
5
10
15
20
θ1
95
90
85
80
75
Задача № 5
Воздух с параметрами t1 и
1
охлаждают при постоянном давлении р=2бар до
температуры t2. Температура t2 меньше температуры точки росы (t2 < tp). Значения
t1,
1
и t2 даны в табл. 5 по вариантам.
Определить уменьшение влагосодержания воздуха (d1-d2) и температуру точки
росы (tp), а также отводимую теплоту в процессе охлаждения (q, кДж/кг с.в.).
Показать процесс охлаждения и изотерму tp в h-d- диаграмме.
Таблица 5
№ варианта
5
10
15
20
25
t1 °C
%
50
80
60
90
40
95
45
85
55
80
t2,°C
10
8
6
8
6
1
61
ЗАДАНИЕ № 4 (к.р. № 1)
Процессы компрессоров
Задача
В компрессоре сжимается газ с начальными параметрами p1=1бap, t1=20°C до
давления р2. Газ, процесс сжатия, число ступеней компрессора, конечное давление
даны в табл. 1 по вариантам. При двух- и трехступенчатом сжатии охлаждение газа
в промежуточных охладителях осуществляется до начальной температуры t1.
Рассчитать температуру газа на выходе из компрессора (Т2), работу, затрачиваемую на сжатие (£кДж/кг), и отводимую теплоту (qотв, кДж/кг).
Теплоемкость газа принять постоянной.
Представить процесс сжатия в р-v и T-s- диаграммах. Задание:
назовите типы компрессоров и укажите характер сжатия для каждого типа
(объемное или динамическое, с отводом тепла или адиабатное).
№
Газ
Сжатие
Число ступеней
р2,
Таблица 1
Показатель
1
вар.
2
Воздух
Политропное
1
Не
Политропное
1
10
бар
10
1,2
политропы
1,4
3
СО2
Политропное
1
10
1,15
4
5
6
7
8
9
10
Н2
N2
Воздух
Не
С02
Н2
N2
Политропное
Политропное
Политропное
Политропное
Политропное
Политропное
Политропное
1
1
2
2
2
2
2
10
10
18
18
18
18
18
1,3
1,25
1,2
1,4
1,15
1,3
1,25
11
Воздух
Политропное
3
27
1,2
12
13
14
15
16
17
18
19
Не
С02
Н2
N2
Воздух
Не
С02
Н2
Политропное
Политропное
Политропное
Политропное
Адиабатное
Адиабатное
Адиабатное
Адиабатное
3
3
3
3
2
2
2
2
27
27
27
27
18
18
18
18
1,4
1,15
1,3
1,25
62
1
20
21
22
23
24
25
2
N2
Воздух
Не
СО2
Н2
N2
3
Адиабатное
Адиабатное
Адиабатное
Адиабатное
Адиабатное
Адиабатное
4
2
3
3
3
3
3
5
18
27
27
27
27
27
6
-
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Сколько кг воздуха находится в комнате размерами 4x6x2,5 м3 при
атмосферном давлении р=745 мм рт. ст. и температуре 20 °С?
2.Какова плотность воздуха при нормальных физических условиях:
р=760мм рт. ст., t=0°C?
3.Какова плотность метана (CH4) при нормальных физических условиях:
р=760 мм рт.ст., t=0 °C? Сравните с плотностью воздуха при тех же условиях.
4.Каков объем 1 киломоля воздуха при р=700 мм рт. ст., t=30 °C?
5.Массовая
производительность
компрессора
G=500
кг/ч.
Параметры
сжатого воздуха р=20 бар, t=130°C. Какова объемная производительность
(V, м3/с)? Сравните с объемной производительностью при нормальных
физических условиях (р=760мм рт. ст., t=0°C).
6.Во сколько раз масса аэростата, заполненного гелием, меньше массы
аэростата, заполненного воздухом,
если давление газа
р=750 мм рт. ст.,
t=20 °C, объем аэростата V=4000м3, масса оболочки аэростата М0=700 кг,
мольные массы гелия и воздуха равны соответственно 4 кг/кмоль
и
29 кг/кмоль.
7.Если на одну чашку весов в условиях вакуума поставить килограммовую
гирю, то какой объем воздуха уравновесит весы? Давление воздуха
р=750 мм рт.ст., температура воздуха 25 °С.
8.Во сколько раз отличается плотность воздуха при атмосферном давлении
р=745мм рт.ст. и температурах t1=-20°C и t2=30°С?
9.Сравните массы воздуха
в
и летом. Объем помещения V=5 х
неотапливаемом помещении
10 х Зм3, атмосферное
зимой
давление
р=740мм рт.ст., температура: зимой t1=-20 "С, летом t2=25 °С.
63
10.Сравните плотность атмосферного воздуха при р=760 мм рт.ст. и
температурах t1=-20°C и t2=30°C?
баллона с углекислым газом V=0,5
11.Объем
м3, давление
газа
р=10 бар, температура t=20 °С. Какова масса газа в баллоне?
12.Какой объем занимают 10 киломолей азота (N2) при нормальных
физических условиях: р=760 мм рт. ст., t=0°C?
13.Какова мольная масса газовой смеси СО2 и СО, если массовая доля
g CO 2 = 0,45? Какова объемная доля rCO2 ?
14.Какова газовая постоянная смеси азота (N2) с водородом (Н2), если
давление смеси р=3 бар, парциальное давление азота p N 2 =2 бар?
15.Какова газовая постоянная смеси водорода (Н 2) и окиси углерода
(СО), если массовая доля водорода g H 2 =0,667?
16.Газовая смесь содержит 10 кг кислорода (О2) и 15кг азота (N2). Определить газовую постоянную смеси (R) и плотность р при нормальных физических условиях: р=760 мм рт. ст., t=0 °C?
17.Объемный состав воздуха: rO2 =0,21, rN2 =0,79. Каков массовый состав
воздуха ( g O g N )?
2
2
18.Объемный
rCO =0,005,
состав
продуктов
rN2 =0,705, rН 2O = 0,1
сгорания:
rCO2 =0,12,
rO2 =0,07,
давление р=10 бар, температура t=1000°C.
Какова плотность продуктов сгорания?
19.Газовая смесь состоит из двух киломолей углекислого газа (СО2) и
трех киломолей гелия (Не). Какова масса газовой смеси (М, кг) и газовая постоянная (R, Дж/кг-К)? Мольная масса гелия μ=4кг/кмоль.
20.В смеси содержится 5кг углекислого газа (СО2) и 2кг окиси углерода
(СО). Давление смеси р=2 бар. Какова газовая постоянная смеси (R,
Дж/кг-К) и парциальное давление рСО2 ?
21.Газовая смесь состоит из четырех киломолей аммиака (NН3) и одного
киломоля азота (N2). Какова газовая постоянная смеси (R, Дж/кг-К)?
22.В газовой смеси содержится метан
(СН 4) и азот (N2).
Массы
64
компонентов одинаковы. Чему равна газовая постоянная смеси (R, Дж/кг-К)?
23.В газовой смеси содержатся аммиак (NH3) и азот (N2), парциальные
объемы компонентов одинаковы.
Чему равна газовая постоянная смеси
(R, Дж/кг-К)?
24.Газовая смесь состоит из углекислого газа (СО2) и двуокиси серы
(SO2). Число киломолей компонентов одинаково. Чему равна мольная масса
газовой смеси?
25.Для воздуха и углекислого газа (СО 2) оцените отклонение в %
мольных теплоемкостей μCv при температурах 100 °С и 1000 °С от постоянных
значений μсv (20,8кДж/кмоль-К для двухатомных газов и 29,1 - для
трех- и многоатомных газов). Воспользуйтесь таблицами 1 и 3 ПРИЛОЖЕНИЯ
в учебном пособии. Сделайте выводы.
26.При нагреве воздуха от t1=50°C до t2=250°С определите изменение
внутренней энергии (∆u) тремя способами:
• используя табличные значения u,
• используя средне-арифметическое значение теплоемкости сv для данного
интервала температур,
• приняв
теплоемкость
постоянной,
согласно
молекулярно-
кинетической теории газов.
Воспользуйтесь табл.1 ПРИЛОЖЕНИЯ учебного пособия [7]. Сравните
полученные результаты. Какое значение
u и является наиболее точным и
почему?
27.Выполните задание вопроса № 26 для углекислого газа (СО2).
28.Определите изменение
энтальпии ( h )
при
нагреве
воздуха
от
t1=100°C до 800°С тремя способами:
• используя табличные значения h,
• используя средне-арифметическое значение теплоемкости ср для данного
интервала температур,
• приняв
теплоемкость
постоянной,
согласно
молекулярно-
кинетической теории газов.
65
Воспользуйтесь табл. 1 ПРИЛОЖЕНИЯ учебного пособия [7]. Сравните
полученные результаты. Какое значение
h является наиболее точным и
почему?
29.Выполните задание вопроса № 28 для углекислого газа (СО2).
30.Определите изменение энтропии ( s ) при нагреве воздуха в изобар
ном (p=const) процессе от t1=0 °C до t2=500 °С тремя способами:
• используя табличные значения s°,
• используя средне-арифметическое значение теплоемкости ср для данного
интервала температур,
• приняв
теплоемкость
постоянной,
согласно
молекулярно-
кинетической теории газов.
Воспользуйтесь табл. 1 ПРИЛОЖЕНИЯ учебного пособия [7]. Сравните
полученные результаты. Какое значение ∆s является наиболее точным и почему?
31.Выполните задание вопроса № 30 для углекислого газа (СО2).
32.Для воздуха в интервале температур 100-600 °С найдите среднюю
изобарную теплоемкость ср, кДж/кг-К тремя способами:
• используя истинные значения теплоемкостей μср при данных температурах
(средне-арифметическое значение),
• используя табличные значения энтальпий h,
• используя постоянное значение теплоемкости для двухатомных газов
μcv =20,8 кДж/кмоль-К. Воспользуйтесь табл. 1 ПРИЛОЖЕНИЯ учебного
пособия [7]. Сравните полученные значения. Какое значение теплоемкости является наиболее точным и почему?
33.Выполните задание вопроса № 32 для углекислого газа (СО2).
Рассчитайте изохорную теплоемкость ср, кДж/кг-К смеси газов СО2
и N2 при t=500 0С, если rCO2 =0,28. Воспользуйтесь таблицами 2 и 3 ПРИЛОЖЕНИЯ учебного пособия [7].
35.Рассчитайте изохорную теплоемкость cv, кДж/кг-К смеси газов СО2
66
и N2 при t=500 °С, если g N 2 =0,46. Воспользуйтесь таблицами 2 и 3 ПРИЛОЖЕНИЯ учебного пособия [7].
36.Определите энтропию газовой смеси СО2
и N2
при t=300 °C, р=5
бар, если g CO 2 =0,35. Воспользуйтесь таблицами 2 и 3 ПРИЛОЖЕНИЯ учебного пособия [7].
37.10 кг воды с температурой t=10°C нагревается при давлении р=1бар
до температуры кипения (ts). Сколько тепла (Q, кДж) требуется для нагрева?
Покажите процесс нагрева воды в T-s- диаграмме.
38.Сколько тепла необходимо сообщить, чтобы испарить 2кг кипящей
воды при давлении 5 бар? Покажите процесс испарения воды в р-υ и
T-s- диаграммах.
39.Чему равна плотность (ρ, кг/м3) и внутренняя энергия (u, кДж/кг)
мокрого пара с давлением р=5 бар и степенью сухости х=0,8? Как изменится
плотность, если пар станет сухим насыщенным при р=5бар? Покажите оба
состояния в h-s- диаграмме.
40.Как изменяется теплота парообразования (r, кДж/кг) с увеличением
давления пара? При каком давлении теплота парообразования равна 0? Какой
площадью характеризуется теплота парообразования в T-s- диаграмме?
41.Объем мокрого пара с параметрами р=2 бар, х=0,725 равен V=2м3.
Чему равна масса мокрого пара? Покажите состояние мокрого пара в р-v и
T-s- диаграммах.
42.Приведите значения параметров критического состояния для воды и
водяного пара: ркр , υкр, tKp, hкр , sKp .Определите параметры (х, h, υ) для со
стояния при р=1 бар и s=sKp. Покажите в диаграмме T-s это состояние.
43.Определите, в каком состоянии находится Н2О при давлении р=80
бар и температуре t=320C. Рассчитайте внутреннюю энергию (u, кДж/кг).
Покажите состояние в T-s- диаграмме.
Сколько теплоты надо затратить, чтобы нагреть и испарить 1кг воды с
температурой t=10 °C при постоянном давлении р=5 бар? Покажите
процесс в р-υ и T-s- диаграммах
67
45.При каком давлении (р) изохора υ=0,37481м3/кг пересекает нижнюю
пограничную кривую? Рассчитайте внутреннюю энергию в этом состоянии (u,
кДж/кг). Покажите изохору и состояние в р-υ -диаграмме.
46.При каком давлении (р) изохора υ=0,37481м3/кг пересекает верхнюю
пограничную кривую? Определите параметры в этом состоянии (h, u, s)
Покажите изохору и состояние в р-υ - диаграмме.
47.При
каком
давлении
(р)
адиабата
s=5,8878
кДж/кг-К
пересекает
верхнюю пограничную кривую? Определите параметры в этом состоянии (h,
t, u). Покажите адиабату и состояние в T-s- диаграмме.
48.При
какой
температуре
(t)адиабата
s=1,4185кДж/кг-К
пересекает
нижнюю пограничную кривую? Определите параметры в этом состоянии (р,u).
Покажите адиабату и состояние в T-s- диаграмме.
КОНТРОЛЬНАЯ РАБОТА № 2
ЗАДАНИЕ № 1 (к.р. № 2)
Расчет обратимого цикла газового двигателя
Задача
Рассчитать цикл газового двигателя: двигателя вyутреннего сгорания (ДВС)
или газотурбинного двигателя (ГТД), рис. 2.1.
Номер цикла, а также исходные данные для расчета приведены в табл. 1 по
вариантам. Размерность величин, приведенных в табл. 1: р[бар], υ[м3/кт] t[oC].
Принять, что рабочее тело обладает свойствами воздуха.
Рассчитать параметры (р, υ, Т) в узловых точках цикла, подведенную (q1),
отведенную (q2) теплоту, работу (ℓ) и термический КПД (
t
) цикла.
Теплоемкость воздуха принять постоянной. Показать цикл в T-s- диаграмме. Результаты расчета представить в виде табл.2.
Ответить на вопросы:
• для вариантов с расчетом цикла ДВС:
1) чем отличается обратимый цикл ДВС от реального?
68
2)Как влияет степень сжатия
и начальные параметры рабочего тела
1
2
(р1 Т1) на термический КПД цикла?
• Для вариантов с расчетом цикла ГТД:
1)приведите схему ГТД для Вашего варианта.
2)В чем состоят преимущества и недостатки газотурбинных двигателей
по сравнению с ДВС?
Рис. 2.1
Таблица 1
№
№
вар. цикла
1
5 р1=0,8
2
2 р1=1,0
3
1 р1=1,0
4
5 р1=1,0
5
4 р1=1,0
6
5 t1=37
7
1 р1=1,0
8
5 t1=60
9
5 р1=1,0
t1=-12
t1=30
υ1=l,09
t1=27
t1=20
t3=950
t1=20
р2=8
t3=950
2/p,=7
υ=p
2=0,124
р2=12,3
р2=10
t2=220
р1=5
υ2=0,233
t2=320
р2=7
p3=30,5 υ4=0,149
t3=952
t3=1000
t3=1350
p2=25
р3=20
υ4=2,4
Исходные данные
p 2 / p1
7
3
3
/
/
10
1
р1=1,0
υ1=0,84
р2=6
t3=1355
11
12
13
14
15
16
17
18
5
4
5
2
5
2
3
1
р1=1,2
р1=1,0
р1=1,0
р1=1,0
t1=60
р1=1,0
р1=1,0
р1=1,0
t1=20
t1=27
t1=17
υ1=0,861
t4=1800
t1=20
tu1=70,
3=0,1322
р2=50
р2=6
p2=10
t3=600
t3=700
р1=1,0
υ3=0,1322
t3=1000
t3=1000
p2=8
p2=10
V1 / V2
p4=70
1
/
2
2
2
2.8
2,2
15,
р3 / р2
1,5
u2=0,0661
12
V3 / V 2
1,67
p5=3,8 t1=0
69
1
19
20
2
3
2
3
р1=1,0
р1=0,9
4
t1=15
t1=10
5
t2=220
t3=800
21
22
23
3
1
5
р1=1,0
р1=1,0
р1=1,0
υ=0,87
t1=15
t1=15
р2=15,2
t3=780
p2=5,5
t3=1047 υ4=0,149
p2=4,8
24
3
р1=1,0
υ1=0,84
р1=35,l
t3=1345
υ2=0,17
t3=1000
5 υ1=0,879 р1=1,0
25
6
t4=400
p2=6
р3 / р2
3,5
Таблица 2
Точки
р
бар
υ
м /кг
3
Т
К
q1
q2
кДж/кг
ℓ
t
-
1
2
3
4
5
ЗАДАНИЕ № 1* (к. р. № 2)
Термодинамический анализ цикла энергетической газотурбинной
установки ГТУ - 50 – 800.
При решении данной задачи представляется возможность познакомиться с
системой КПД для оценки степени необратимости реальных циклов и
способами повышения КПД газотурбинных установок.
Решение данной задачи не обязательно, но желательно в целях повышения
уровня знаний по данной дисциплине.
Задача
На рис. 2.2 и 2.3 приведены схема и цикл ГТУ -50-800, предназначенной для
выработки электроэнергии, электрическая мощность Nэ=50MBx, максимальная
температура газов t=800°C.
70
Рис. 2.2
Обозначения: К1 , К2. К3 - ступени трехступенчатого компрессора, Т1 , Т2 ступени двухступенчатой турбины, ПО1 , ПО2: - промежуточные охладители,
КС1, KC2 - камеры сгорания, Р - регенератор, ЭГ - электрический генератор.
Цифры на схеме соответствуют узловым точкам действительного цикла.
Рис. 2.3
Установка представляет собой двухвальный агрегат с тремя ступенями
сжатия, двумя ступенями расширения и регенерацией тепла. Цикл состоит из
адиабатных процессов сжатия и расширения рабочего тела и изобарных процессов подвода и отвода тепла.
В действительных (необратимых адиабатных) процессах сжатия и расширения рабочего тела энтропия увеличивается (процессы 1-2, 3-4, 5-6, 8-9,
10-11). Конечные точки обратимых адиабатных (s=const) и изобарных
процессов обозначены одним штрихом (2', 4', 6', 9', 11', 7', 12').
71
Дано:
• параметры воздуха на входе в первую ступень компрессора р1=1бар,
t1=20°C;
• температуры воздуха на входе во вторую и третью ступени компрессора
t3=t5=tl=20°C;
• степени повышения давления в ступенях компрессора β1= β2= β3=2,62;
• температуры продуктов сгорания на входе в ступени турбины
t8=t10=800°C;
• степени понижения давления в ступенях турбины одинаковы β4= β5;
• коэффициент регенерации ζ=0,75;
• внутренний относительный КПД ступеней компрессора ηoiк=0,8;
• внутренний относительный КПД ступеней турбины ηoiт =0,85;
• КПД камеры сгорания ηkc =0,96;
• механический КПД ступеней турбины ηмт=0,98;
• механический КПД ступеней компрессора ηмк =0,97;
• КПД регенератора ηp=0,96;
КПД генератора электрического тока ηr=0,99;
Рассчитать:
• температуры в узловых точках обратимого цикла (2’, 4', 6', 7', 9',11',
12');
• подводимую (q1 кДж/кг) отводимую (q2 кДж/кг) теплоту и термический
КПД (ηt) обратимого цикла;
• температуры в узловых точках действительного цикла (2, 4, 6, 7, 9,11,
12);
• подводимую (q1д, кДж/кг), отводимую (q2д, кДж/кг) теплоту и внутренний
КПД (ηi) действительного цикла;
• эффективную работу (ℓе ,кДж/кг) газотурбинной установки;
• электрическую работу (ℓэ ,кДж/кг) ГТУ;
• теплоту, выделившуюся при сгорании топлива (q', кДж/кг);
• электрический КПД (ηэ) газотурбинной установки.
Принять, что рабочее тело обладает свойствами воздуха. Расчеты произвести
72
при постоянной теплоемкости μсv=20.8 кДж/кмоль-К.
• Сравните полученные значения термического (ηt), внутреннего (ηi) и
электрического (ηэ) коэффициентов полезного действия и сделайте выводы.
• Сравните электрический КПД газотурбинной установки с эффективным
КПД газотурбинного двигателя с циклом Брайтона и сделайте выводы.
Ответы выделите. Найденные значения температур в узловых точках
обратимого и необратимого циклов представьте в виде таблицы. Приведите
ответы по всем величинам, которые требуется рассчитать.
ЗАДАНИЕ № 2 (к. р. № 2)
Расчет обратимого цикла паротурбинной установки
Задача
Рассчитать обратимый цикл Ренкина (рис. 2.4). Параметры пара на входе в
турбину р1, t1 и давление пара на выходе из турбины р 2 даны в табл. 1 по
вариантам.
Порядок решения задачи:
1. Представить цикл в T-s- и h-s- диаграммах.
Привести схему установки и нанести узловые точки цикла на схему.
Указать назначение каждого процесса (1-2, 2-3 и т.д.), его характер (адиабатный,
изобарно - изотермический) и т.д.).
Рис. 2.4.
3. Определить параметры р, t, h, s, x в узловых точках цикла с использованием
таблиц [3] и занести в табл. 2.
4. Рассчитать подводимую теплоту (q1), отводимую теплоту (q2), работу турбины (ℓт), работу насоса (ℓи), работу цикла (ℓ), термический КПД цикла (ηt)
73
5. Показать цикл Карно в р-υ и T-s- диаграммах для интервала давлений
р1 ÷ р2. Сравнить термический КПД цикла Ренкина (ηt,) с термическим КПД
цикла Карно (ηtк).
6.Ответить на вопросы:
• Почему нецелесообразно осуществление цикла Карно в паротурбинной
установке?
• Как зависит термический КПД цикла Ренкина (ηt) от параметров пара на
входе в турбину p1, t1, от давления в конденсаторе р2?
Таблица 1
№ вар.
1
2
3
4
5
6
7
8
9
10
р1, бар
100
120
140
160
200
100
120
140
160
200
t1, 0С
360
ti,
С
400
440
480
520
400
440
480
520
560
р2, бар
0,04
0,04
0,04
0,04
0,04
0,03
0,03
0,03
0,03
0,03
11
12
13
14
15
100
120
140
160
200
440
480
520
560
600
0,05
0,05
0,05
0,05
0,05
16
17
18
19
20
21
22
23
24
25
100
120
140
160
200
100
120
140
160
200
440
400
520
480
560
360
400
440
480
520
0,04
0,04
0,04
0,04
0,04
0,03
0,03
0,03
0,03
0,03
74
Таблица 2
Точки
1
2
3
4
5
р, бар
t,°C
h, кДж/кг
s, кДж/кг-К
х
ЗАДАНИЕ №2'(к. р. № 2)
Способы повышения КПД паротурбинных установок
Такими способами являются: применение промежуточного перегрева пара
(задача № 1), регенерации тепла (задача № 2), а также совместная выработка
электроэнергии и тепла на теплофикационных паротурбинных установках
(задача № 3). При решении данных задач представляется возможность
разобраться с системой КПД для оценки эффективности реальных циклов
паротурбинных установок.
Решение данных задач не обязательно, но желательно в целях повышения
уровня знаний по дисциплине.
Задача № 1
На рис. 2.5 и 2.6 представлены схема и цикл паротурбинной установки с
промежуточным перегревом пара.
Дано: параметры пара перед СВД: р1=100 бар, t1=550°C; параметры пара на
входе в СНД: р 3 =30 бар, t3 =t1 давление пара в конденсаторе р4=0,04 бар;
КПД парового котла ηпк=0,9, внутренний относительный КПД обеих ступеней
турбины одинаков ηоiт =0,85, механический КПД ηм=0,98, КПД электрического
генератора ηr=0,99.
75
Рис.2.5
Рис. 2.6
Обозначения: ПК - паровой котел, П - пароперегреватель, ПП промежуточный пароперегреватель, СВД, СНД - ступени высокого и низкого
давлений турбины, К- конденсатор, ЭГ - электрический генератор, Н - насос.
Цифры на схеме соответствуют узловым точкам действительного цикла (рис. 2.6).
76
Рассчитать:
• значения энтальпий (h) в узловых точках обратимого и действительного
циклов;
• термический КПД обратимого цикла (ηt), внутренний КПД действительного цикла (ηi), электрический КПД ηэ турбогенераторной установки;
• потери тепла в паровом котле (qпотпк), в конденсаторе (qпотк);
• механические потери в ступенях турбины (ℓ тпoт. мех);
•
потери в генераторе электрического тока (ℓ гпот).
Записать уравнение теплового баланса и проверить тождество.
Проанализировать полученные результаты и сделать выводы.
Задача № 2
На рис. 2.7 и 2.8 представлены схема и регенеративный цикл паротурбинной установки с одним отбором пара в смешивающий подогреватель.
Рис.2.7.
Рис.2.8.
Обозначения: ПК - паровой котел, П - пароперегреватель, Т- паровая
турбина, ЭГ - электрогенератор, К - конденсатор, ПB - подогреватель воды,
Н - насос.
Цифры на схеме соответствуют узловым точкам обратимого цикла, представленного в T-s- диаграмме.
Дано: параметры пара перед турбиной: p1=140 бар, t1=550°C; давление пара
в конденсаторе р 3=0,04бар; давление отбора пара из турбины р2=р5=6 бар.
77
Рассчитать: подводимую теплоту (q1), отводимую теплоту (q2), термический
КПД обратимого регенеративного цикла (ηtрег).
Рассчитать термический КПД (ηt) цикла без регенерации (1-3-4), сравнить с
термическим КПД регенеративного цикла (ηtрег).сделать выводы.
Задача № 3
На рис. 2.9. и 2.10 представлены схема и цикл теплофикационной
паротурбинной установки с регулируемым отбором пара.
Рис. 2.9
Рис. 2.10
Обозначения: ПК - паровой котел, П - пароперегреватель, Т - паровая
турбина, ЭГ - электрогенератор, ПТ - потребитель тепла, К - конденсатор, ПБ
- питательный бак, Н - насос.
Цифры на схеме соответствуют узловым точкам обратимого цикла,
представленного в T-s- диаграмме.
Дано: параметры пара перед турбиной: p1=180 бар, t1=550°C; давление
отбора пара р2=9 бар; давление пара в конденсаторе р3=0,04 бар; расход пара,
поступающего на турбину, G=280 кг/с; расход пара, направляемого потребителю
Gотб=160 кг/с; температура возвращаемого потребителем конденсата tK=100°C
при давлении р2=9 бар.
Рассчитать:
• значения энтальпий в узловых точках цикла;
• теоретическую мощность обратимого цикла (Nt, кВт);
• теплоту, переданную потребителю (Qпотр, кВт);
78
• подводимую теплоту в обратимом цикле (Q1, кВт);
• коэффициент использования тепла (К) обратимого цикла теплофикационной паротурбинной установки;
• термический КПД обратимого цикла без теплофикационного отбора
пара (ηt).
Рассчитать:
• значения энтальпий в узловых точках цикла;
• теоретическую мощность обратимого цикла (Nt, кВт);
• теплоту, переданную потребителю (Qпотр, кВт);
• подводимую теплоту в обратимом цикле (Q1, кВт);
• коэффициент использования тепла (К) обратимого цикла
теплофикационной паротурбинной установки;
• термический КПД обратимого цикла без теплофикационного отбора
пара (ηt).
Сравнить коэффициент использования тепла (К) теплофикационного цикла с
термическим КПД (ηt). цикла без теплофикационного отбора пара и сделать
выводы.
ЗАДАНИЕ № 2 " (к.р. № 2)
Термодинамический анализ циклов холодильных установок
Предлагается выполнить термодинамический анализ для двух наиболее
распространенных типов холодильных установок: газовых (задача № 1) и
парокомпрессионных (задача № 2).
Решение данных задач не обязательно, но желательно в целях повышения
уровня знаний по дисциплине.
Задача № 1
На рис. 2.11, 2.12 и 2.13 представлены схема и обратимый цикл в р-υ и T-sдиаграммах газовой холодильной машины.
79
Рис. 2.11
Цифры на схеме соответствуют узловым точкам обратимого цикла,
представленного в р-υ и T-s- диаграммах.
Обозначения: К - компрессор, П - привод компрессора, D - детандер, ТО теплообменник-охладитель, ХК - холодильная камера
Рис. 2.12
Дано: хладоагент (ХА)- воздух; параметры ХА на входе в компрессор:
p1=16ap, t1=-20°C; давление ХА на выходе из компрессора р2=6 бар; температура
ХА на выходе теплообменника-охладителя t3=20°С.
Рассчитать:
• температуры воздуха в узловых точках цикла;
• работу, затрачиваемую на компрессор (ℓ к ,кДж/кг);
• работу, получаемую в детандере (ℓD ,кДж/кг);
• работу обратимого цикла (ℓ,кДж/кг);
• удельную холодопроизводительность обратимого цикла (qx, кДж/кг);
• удельную теплоту, передаваемую в окружающую среду (q0, кДж/кг);
• холодильный коэффициент обратимого цикла (ε);
• холодильный коэффициент идеального цикла Карно (εк) для интервала
80
температур (ТОС ÷ТХ);
• эксергетический КПД обратимого цикла холодильной машины (ηэкс).
Теплоемкость воздуха принять постоянной (μсv=20,8кДж/кмоль-К).
Ответы выделить и на основании полученных результатов расчета сделать
выводы.
Задача № 2
На рис. 2.14 и 2.15 представлены схема и обратимый цикл
парокомпрессионной холодильной установки.
Рис.2.14
Рис. 2.15
81
Обозначения: К - компрессор, КОН - конденсатор, охлаждаемый водой, ОБ охлаждающая вода, ДВ - дроссельный вентиль, И - испаритель, ХЛ хладоноситель, П - привод компрессора.
Цифры на схеме соответствуют узловым точкам обратимого цикла,
представленного в T-s- диаграмме.
Дано: хладоагент - фреон-12, температура хладоагента на входе в компрессор t1=-20°C, на выходе из компрессора: t2=20°C, x2=l.
Рассчитать:
• значения энтальпий (h) в узловых точках обратимого цикла;
• затрачиваемую работу в цикле (ℓ)
• удельную холодопроизводительность цикла (qx);
• холодильные коэффициенты для обратимого цикла 1-2-3-4 (Е) и цикла
Карно 1-2-3- га (εк) в интервале температур Тос - Тх;
• эксергетический КПД обратимого цикла (ηэкс).
На основании полученных результатов расчета сделать выводы относительно
термодинамического совершенства обратимых циклов парокомпрессионных
холодильных машин.
При
расчете
энтальпий
воспользоваться
табл.8
(термодинамические
свойства фреона-12 в состоянии насыщения), приведенной в ПРИЛОЖЕНИИ
учебного пособия [7].
ЗАДАНИЕ № 3 (к. р. № 2)
Расчет стационарной теплопроводности и теплопередачи
Задание № 3 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Через кирпичную стену передается теплота. Постоянные температуры на
поверхностях стены t1 и t2, коэффициент теплопроводности кирпича (λ),
толщина стены ( ), площадь изотермической поверхности (F) даны в табл. 1 по
вариантам.
82
Рассчитать:
• плотность теплового потока (q, Вт/м ),
• теплоту, переданную через стену за сутки (Q, Дж),
•
координату изотермической поверхности (Х0) с температурой t=0°C.
Ответы выделить. Изобразить схематично график распределения температур по
толщине стены.
Таблица 1
№ вар.
1
6
11
16
21
, см
40
35
45
50
40
15
0,14
20
-10
20
0,2
25
-15
25
0,3
18
-20
30
0,8
23
-25
35
0,5
22
-30
F,м2
λ, Вт/м К
t1,°C
t2,°C
Задача № 2
Теплота передается через стенку трубы толщиной δ=50мм. Постоянные
температуры на внутренней поверхности трубы (t1) и на наружной (t2), a также
коэффициент теплопроводности стенки (λ), внутренний диаметр (d1) и длина (ℓ)
трубы даны в табл.2.
Рассчитать:
• линейную плотность теплового потока (qℓ, Вт/м),
количество теплоты, передаваемой через стенку трубы за одни сутки (Q,ДЖ),
• температуру изотермической поверхности в середине стенки трубы (t), т.е.
при r
r1
r2
2
. Сравнить полученную температуру с t ср
t1
t2
2
, объяснить
причину несовпадения температур t и tcp , показать t и tcp на графике
распределения температур по толщине стенки.
83
Таблица 2
№ вар.
2
7
12
17
22
d1|, мм
50
100
150
200
250
ℓ,м
10
15
20
25
30
λ, Вт/м К
0,2
0,1
0,2
0,1
0,2
t1,.°C
100
150
200
250
300
t2,°C
80
120
160
200
260
Задача № 3
Теплота передается через плоскую стальную стенку с коэффициентом
теплопроводности λc=40 Вт/м-К от дымовых газов к кипящей воде. Толщина
стенки (δc), температура дымовых газов (tж1,), температура воды (tж2), коэффициент теплоотдачи от газов к стенке (а1) и от стенки к воде (а2) даны в табл.3
по вариантам.
Определить:
• коэффициент теплопередачи (К, Вт/м2 ·К) от газов к воде,
• плотность теплового потока, передаваемого через стенку (q, Вт/м2),
• температуры на поверхностях стенки со стороны газов (t1) и со стороны
воды (t2).
Построить график распределения температур по толщине стенки. Нанести на
график температуры tЖ1, и tЖ2 .
В процессе эксплуатации стенка со стороны воды покрылась слоем накипи
толщиной δн коэффициент теплопроводности накипи λн=1,0 Вт/м·К.
Рассчитать для этого случая К, q, t1, t2, температуру на поверхности накипи
(tн). Построить график распределения температур по толщине стенки и накипи.
Дать сравнительный анализ двух графиков.
Данные, необходимые для решения задачи, содержатся в табл.3.
84
Таблица 3
№ вар.
3
8
13
18
23
δс, мм
25
20
15
16
18
δн, мм
1,4
2,6
1,8
1,0
0,8
α1, Вт/м2 К
30
35
40
45
50
а2 , Вт/м2 К
4000
3000
3500
4500
2500
tж1 , °С
1200
1100
1000
960
900
t ж 2 , °С
180
160
150
140
190
Задача № 4
Теплота передается через стенку стальной трубы толщиной δс=3мм
(λс=50 Вт/м·К) от дымовых газов к кипящей воде. Внутренний диаметр трубы
(d1), температура дымовых газов (tж1), температура кипящей воды (tж2),
коэффициент теплоотдачи от дымовых газов к наружной поверхности трубы
(α2), коэффициент теплоотдачи от внутренней поверхности трубы к воде (α2)
даны в табл.4.
Рассчитать:
• коэффициент теплопередачи (К, Вт/ м 2·К) от газов к воде,
• линейную плотность теплового потока (qℓ, Вт/м),
• температуры на внутренней поверхности трубы (t1) и на наружной
поверхности (t2).
Построить график распределения температур по толщине стенки. Нанести на
график температуры t ж1, и t Ж2.
В процессе эксплуатации на внутренней поверхности образовался слой
накипи толщиной (δн).
Рассчитать для этого случая К, qℓ, t1, t2, температуру на поверхности накипи
(tH).
85
Принять коэффициент теплопроводности накипи λн=0,8 Вт/м·К.
Построить график распределения температур по толщине стенки и накипи.
Дать сравнительный анализ двух графиков.
Таблица 4
№ вар.
4
9
14
19
24
d1, мм
0,05
0,1
0,15
0,20
0,25
tж1 ,°С
1200
1100
1000
960
900
tж2 ,°С
180
160
150
140
190
α1, Вт/м2·К
70
80
90
100
85
α2, Вт/м2·К
4000
3000
3500
4500
2500
δн, мм
1,4
2
1,8
1,6
1,5
Задача № 5
По стальному теплоизолированному трубопроводу, расположенному на
открытом воздухе, передается горячий теплоноситель.
Толщина стенки трубы δ=3мм, коэффициент теплопроводности стали
λ=50 Вт/мК. Температура окружающего воздуха tЖ=20°С, коэффициент
теплоотдачи от поверхности изоляции к окружающему воздуху α=10 Вт/м ·К.
Остальные данные, необходимые для расчета: внутренний диаметр трубы
(d1), температура на внутренней поверхности стальной трубы (t1), толщина слоя
изоляции (δиз) и коэффициент теплопроводности изоляции (λиз) даны в табл.5 по
вариантам.
Рассчитать:
• температуру на поверхности изоляции (tИЗ),
• температуру наружной поверхности стальной трубы (t2),
• суточную потерю тепла на участке трубы длиной 100м (Q, Дж).
Ответы выделить. Изобразить схематически график распределения температур
по толщине стенки трубы и по толщине изоляции.
86
Таблица 5
№ вар.
5
10
15
20
25
d|1, мм
150
200
250
300
350
t1 ,°С
180
175
170
165
160
δиз ,мм
40
60
70
80
90
λиз , Вт/м ·К
0,07
0,14
0,1
0,09
0,12
ЗАДАНИЕ № 4 (к. р. № 2)
Расчет нестационарной теплопроводности
Задание № 4 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача №1
Тонкая пластина из пластика толщиной 2δ=6 мм с размерами 2х3м2, с
начальной температурой tН погружается в горячую среду с температурой
tЖ=100°С.
Коэффициент теплопроводности (λ,), теплоемкость (с), плотность (ρ) для
материала пластины, а также постоянный коэффициент теплоотдачи в процессе
нагрева (α) и другие данные, необходимые для расчета, приведены в табл.1 по
вариантам.
Определить температуру в центре (tц) и на поверхности (tп) пластины через
время η1 после погружения пластины в горячую среду.
Изобразить график распределения температуры по толщине пластины для
моментов времени η = 0, η = η1, η = ∞.
Определить полное количество тепла, воспринятого пластиной в процессе
нагрева (Qп, Дж). Ответы выделить.
87
Таблица 1
№ вар.
λ, Вт/мК
1
1
6
1,2
11
1,4
16
1,6
21
1,8
с, Дж/кгК
714
1091
1167
1231
1200
ρ, кг/м3
1400
1100
1200
1300
1500
α,Вт/м К
100
400
187
107
180
tн °С
1 Н ,1 , ^С
10
18
15
27
20
54
25
36
30
45
2
Задача № 2
Длинный стальной вал диаметром d=40 мм с начальной температурой tH
погружается в воду с температурой tЖ.
Свойства стали: теплопроводность λ=40 Вт/мК, теплоемкость
с=460 Дж/кгК, плотность ρ=7900 кг/м3.
Коэффициент теплоотдачи в процессе охлаждения (а) и другие данные,
необходимые для расчета, приведены в табл.2 по вариантам.
Определить температуры в центре (tц) и на поверхности (tп) вала через время
(η1) после его погружения в холодную воду.
Изобразить график распределения температуры по диаметру вала для
моментов времени η=0, η=η1’ η=∞.
Определить полное количество тепла Q п, Дж/м), отданное валом в процессе
охлаждения, в расчете на ℓ = 1м его длины. Ответы выделить.
Таблица 2
№ вар.
2
7
12
17
22
tн , °С
tж,°С
800
5
750
8
600
10
650
12
700
14
α, Вт/м2К
80
120
100
400
440
η1 , мин
5
4
3
2
1,8
88
Задача №3
Длинный металлический стержень диаметром d=50мм с начальной температурой tH помещен в печь с температурой tЖ для термической обработки.
Коэффициент теплопроводности (λ), удельная теплоемкость (с), плотность
(ρ) материала стержня, коэффициент теплоотдачи (α) и другие исходные
данные, необходимые для расчета, приведены в табл.3 по вариантам.
Сколько времени (η1,сек) стержень должен оставаться в печи, чтобы
температура в центре стержня (ηц) достигла заданной величины? Какую температуру в этот момент времени будет иметь поверхность стержня (tп)?
Изобразить график распределения температуры по диаметру вала для
моментов времени η=0, η=η1, η=∞.
Определить полное количество тепла (Qп, Дж/'м), отданное валом в процессе
охлаждения, в расчете на ℓ = 1м его длины. Ответы выделить.
Таблица 3
№ вар.
3
8
13
18
23
tн, °С
20
25
30
35
40
tж , °С
600
655
680
750
800
λ, Вт/мК
45
40
50
45
40
с, Дж/кгК
281
267
320
285
263
ρ, кг/м3
8000
7500
7800
7900
7600
α, Вт/м 2 К
900
1440
1200
720
320
tц, ,°С
513
592
628
607
610
Задача № 4
Нагретый шаровой калориметр из меди диаметром d=50 мм с начальной
температурой tH помещен в воду с температурой tЖ.
Свойства меди: коэффициент теплопроводности λ=384 Вт/мК, удельная
теплоемкость с=381 Дж/кгК, плотность ρ=8800 кг/м3.
Коэффициент теплоотдачи поверхности шара в процессе охлаждения (α) и
другие исходные данные приведены в табл.4 по вариантам.
89
Определить температуры в центре (tu ) и на поверхности шара (tn) через время
(η1) после погружения его в воду.
Изобразить график распределения температуры по диаметру шара для
моментов времени η=0, η= η1, η=∞.
Определить полное количество тепла (Qп, Дж), отданное шаровым калориметром в процессе его охлаждения. Ответы выделить.
Таблица 4
№ вар.
tН ,°С
tж , °С
4
65
5
9
70
10
14
75
15
19
80
20
24
85
18
α, Вт/м2К
η1,с
2300
8,2
3072
10,9
1229
13,6
4608
5,5
614
27,3
Задача № 5
Шаровой калориметр из мрамора диаметром d=50мм с начальной температурой tн охлаждается на открытом воздухе с температурой tЖ.
Свойства мрамора: коэффициент теплопроводности λ,=3,5 Вт/мК, удельная
теплоемкость с=920 Дж/кгК, плотность ρ=2800 кг/м3.
Постоянный коэффициент теплоотдачи в процессе охлаждения (α) и другие
исходные данные приведены в табл.5 по вариантам.
Определить, через какое время (η1 , с) температура в центре шарового
калориметра (tц) достигнет заданного значения. Какая температура в этот
момент времени будет на поверхности шарового калориметра (tп)?
Изобразить график распределения температуры по диаметру шара для
моментов времени η=0, η= η1, η=∞.
Определить полное количество тепла (Qп, Дж), отданное шаровым калориметром в процессе его охлаждения.
90
Таблица 5
№ варианта
tн , °С
tж, °С
α, Вт/м2К
tц,°C
5
90
15
9,8
30
10
95
15
80
20
85
18
8,4
20
14
22
5,6
25,7
24,2
37,7
25
75
25
21
31
КОНТРОЛЬНЫЕ ВОПРОСЫ (к. р. № 2)
1. Поясните, почему циклы в тепловых двигателях совершаются в на
правлении по часовой стрелке, а в холодильных машинах - против часовой
стрелки?
2. Покажите идеальный цикл Карно холодильной машины в T-s - диаграмме. Дайте понятие холодильного коэффициента. Как рассчитать
холодильный коэффициент цикла Карно?
3. Приведите схему и цикл в р-υ
- диаграмме воздушной холодильной
установки. Нанесите на схему узловые точки цикла. Какими площадями
в р-υ -диаграмме характеризуются: а) работа, затрачиваемая на компрессор
(ℓк)>
б) работа, получаемая в детандере (ℓD),
в) результирующая работа
цикла (ℓ)?
4. Приведите цикл воздушной холодильной установки в T-s- диаграмме.
Укажите, в каких узлах установки совершаются процессы цикла. Поясните
физический смысл холодильного коэффициента цикла (ε), приведите
формулу для его расчета.
5. Приведите цикл воздушной холодильной установки в T-s- диаграмме.
Обозначьте температуру вырабатываемого холода (Тх) и температуру
окружающей среды (Тос). Покажите цикл Карно для данного интервала
температур.
Сравните
по
удельной
холодопроизводительности
(qx)
и
затрачиваемой работе (ℓ) обратимый цикл воздушной холодильной установки и
цикл Карно, сделайте выводы.
6. Приведите схему и цикл парокомпрессионной холодильной установки
в T-s- диаграмме. Нанесите узловые точки цикла на схему. Какими
площадями в T-s- диаграмме характеризуются: а) удельная холодопроизво91
дительность (qx), б) теплота, отводимая в конденсаторе (q0)?
7. Приведите
цикл
парокомпрессионной
холодильной
установки
в
T-s- диаграмме. Укажите, в каких узлах установки совершаются процессы
цикла. Поясните физический смысл холодильного коэффициента цикла (е),
приведите формулу для его расчета.
8. В учебнике [1] на рис. 3-10, с. 378 приведен цикл парокомпрессионной
холодильной установки. Как изменится удельная холодопроизводительность
цикла (qx), если хладоагент испарять полностью до х3=1? Приведите
такой цикл в T-s -диаграмме. Сделайте выводы.
9. В учебнике [1] на рис. 3-10, с. 378 приведен цикл парокомпрессионной
холодильной установки.
Сравните
по удельной
холодопроизводитель-
ности (qx) обратимый цикл этой установки и идеальный цикл Карно для
данного интервала температур. Покажите площади, которыми характеризуется удельная холодопроизводительность (qx) этих циклов.
10. Возможно ли осуществить изотермические процессы подвода и от
вода тепла в циклах:
а) парокомпрессионной холодильной установки,
б) воздушной холодильной установки?
11.Каково назначение теплового насоса? Дайте понятие отопительного
коэффициента. Как вычислить отопительный коэффициент идеального цикла
Карно?
12. На рис. 2. приведены три идеальных цикла Карно. Для каких устройств даны
эти циклы?
Рис. 2.16
Обозначения:
Тх – температура охлаждаемого тела;
Тт – температура нагреваемого тела;
Тос – температура окружающей среды.
92
13.Каков механизм передачи тепла теплопроводностью в газах? От каких
факторов зависит коэффициент теплопроводности газов? Сравните коэффициенты теплопроводности легких и тяжелых газов.
14.Каков механизм передачи тепла теплопроводностью в металлах?
Как зависит коэффициент теплопроводности от температуры для чистых металлов, для сплавов?
15.От каких факторов зависит коэффициент теплопроводности строительных и теплоизоляционных материалов? В каких пределах он изменяется? Приведите значения коэффициентов теплопроводности для кирпича,
стекловаты, асбеста [4], табл.3, с. 401.
16.Каков механизм передачи тепла теплопроводностью в жидкостях?
От каких факторов зависит коэффициент теплопроводности жидкостей?
Приведите пределы изменения λ для жидкостей.
17.Дайте понятие коэффициента температуропроводности. Как он обозначается, какую имеет размерность, что характеризует, от каких факторов
зависит? Рассчитайте коэффициент температуропроводности для шлакобетона и льда при t=0°C. Воспользуйтесь [4], табл. 3, с. 401-402.
18.Дайте
понятие
температурного
поля.
Приведите
практические
примеры температурных полей: 1) стационарного одномерного, 2) нестационарного одномерного,
3) стационарного трехмерного, 4) нестационарного
двухмерного.
19.Дайте
полную
характеристику
дифференциального
уравнения
1.27 [4, с. 19], поясните все величины, входящие в уравнение; укажите, какие
процессы передачи тепла и в каких телах описывает данное уравнение.
20.Какие процессы передачи тепла и в каких телах описывает уравнение
1.27 [4, с. 19]? Запишите это уравнение для стационарной теплопроводности в телах:
а) с внутренними источниками тепла, б) без внутренних ис-
точников тепла. Приведите примеры таких процессов.
21.Что включают в себя условия однозначности? Для чего они нужны?
22.Как формулируются граничные условия первого, второго и третьего
рода? Для чего они присоединяются к дифференциальному уравнению?
93
23.Приведите математическое выражение закона Фурье: а) для тепло
вого потока Q, Вт, б) для плотности теплового потока q, Вт/м2. Какой способ
передачи тепла описывает закон Фурье? Чем объяснить знак (-) в правой
части уравнения Фурье?
24.Дайте
понятие
изотермической
поверхности.
Могут
ли
две
изотермические поверхности пересекаться? Какое направление называется
нормалью к изотермической поверхности? Сравните между собой градиенты
температуры
по
нормали
и
по любому другому
направлению
к
изотермической поверхности.
25.Что описывают уравнения (2.3)
и
(2.4), приведенные в [4, с.25]?
Что рассчитывается по уравнениям (2.7) и (2.9.)? Запишите указанные уравнения, дайте все пояснения, приведите рисунок.
26.Что рассчитывается по уравнению (2.22), приведенному в [4, с.30]?
Как называются слагаемые знаменателя этого уравнения и как они связаны с
перепадами температур (tж1 - tc1), (t c1 - tc2), (tc2- tж2)? Дайте понятие коэффициента теплопередачи плоской стенки. Запишите все - tc уравнения с пояснениями, приведите рисунок.
27.Запишите уравнение, по которому можно рассчитать плотность теплового потока q, Вт/м2, передаваемого от среды с температурой tж1 в среду с
температурой tж2 через трехслойную плоскую стенку. Приведите график перепадов температур для условия: a 1 »a2, λ 1 » λ2, λ 1 »λ3, λ2 >λ3.
28.Что описывают уравнения (2.35) и (2.36), приведенные в [4], с.33?
Что рассчитывается по уравнениям (2.39)
и (2.40)? Запишите указанные
уравнения, дайте все пояснения, приведите рисунок.
29.Что рассчитывается по уравнению (2.49), приведенному в [4], с.36?
Запишите уравнение с пояснением, приведите рисунок. Можно ли расчет теплопередачи через цилиндрическую стенку производить по уравнению для
плоской стенки?
30.Запишите уравнение, по которому можно рассчитать линейную
плотность теплового потока (qℓ, Вт/м), передаваемого от горячей воды с
температурой tж1, к окружающему воздуху с температурой tж2 через стенку
94
трубы, покрытой одним слоем тепловой изоляции. Приведите график перепадов температур для условия: a 1 »а 2 , λ ТР »λ из .
31. Дайте понятие критического диаметра изоляции. Как изменятся теплопотери (Q, Вт), если наложить изоляцию на трубу, наружный диаметр
которой: a) d2<dKp,
б) d2=dKp,
в) d2>dKp?
32.Что описывают уравнения (2.61) и (2.62), приведенные в [4], с.40?
Что рассчитывается по уравнениям (2.64) и (2.65)? Запишите указанные
уравнения, дайте все пояснения, приведите рисунок.
33.Что рассчитывается по уравнению (2.66), приведенному в [4], с.41?
Запишите уравнение с пояснением, приведите рисунок.
34.Что рассчитывается по уравнениям (2.90) и (2.87), приведенным в
[4], с.49-50? Поясните все величины, входящие в уравнения, приведите
рисунок.
35.Что рассчитывается по уравнению (2.85), приведенному в [4], с.41?
Запишите это уравнение и поясните все величины его правой части. Дайте
рисунок с расстановкой размеров.
36.Какими способами можно увеличить тепловой поток Q, Вт, переда
ваемый через стенку от среды с температурой tж1 среде с температурой tж2
при условии, что a 1 » а 2 ?
37.Приведите примеры тел и систем с внутренними источниками тепла. Поясните смысл величины qv, Вт/м3. Рассчитайте значение qv для про
водника электрического тока диаметром d=5мм, длиной ℓ=10м при напряжении U=220B и силе тока І=2А.
38.Что описывают уравнения (2.133) и
(2.134), приведенные в [4],
с.59? Что рассчитывается по уравнениям (2.137), (2.138), (2.141)? Запишите
указанные уравнения, дайте необходимые пояснения, приведите рисунок.
39.Что описывают уравнения (2.143) и
(2.144), приведенные в [4],
с.61? Что рассчитывается по уравнениям (2.147), (2.147'), (2.148)? Запишите
указанные уравнения, дайте необходимые пояснения, приведите рисунок.
40.Что рассчитывается по уравнению (2.153), приведенному в [4], с.64?
Запишите уравнение, приведите рисунок. Найдите ошибки в уравнении
95
(2.158) и запишите его правильно.
41. Что рассчитывается по уравнению (2.159), приведенному в [4], с.64?
Запишите уравнение, приведите рисунок. Запишите уравнения для расчета
температур на поверхностях стенки t c1 и tc2.
42. В учебнике [4] рассматриваются следующие классические задачи
стационарной теплопроводности с внутренним тепловыделением: 1. Пластина при симметричных условиях охлаждения. Перечислите еще 4 задачи.
43.Стационарное температурное поле цилиндрического стержня и тру
бы с внутренними источниками тепла описывается одинаковым дифференциальным уравнением. Запишите это уравнение. На примере цилиндрического стержня поясните физический смысл граничных условий.
44.В учебнике [4] на рис. 2.24, с.59 показано температурное поле пластины с
внутренним тепловыделением при симметричных условиях охлаждения (а, tЖ).
Покажите график изменения температуры по толщине пластины для условия:
a 1 >a,tж1=tж2.
45. При
математическом
описании
процессов
теплопроводности
цилиндрического стержня и трубы с внутренними источниками тепла
применяются уравнения:
dt
dr
r
=0,
0
dt
dr
r
=0,
r1
dt
dr
r
=0,
r2
dt
dr
r r0
=0.
Поясните физический смысл уравнений.
46.Для цилиндрического стержня с внутренним тепловыделением да
но: qv, ℓ, d. Как рассчитать:
а) тепловой поток (Q, Вт), рассеиваемый
поверхностью охлаждения стержня,
б) плотность теплового потока
(q, Вт/м2), рассеиваемого с 1 м2 поверхности охлаждения?
47.Для цилиндрической стенки (трубы) с внутренним тепловыделением
и охлаждением только по наружной поверхности дано: qv, r 1 ,
рассчитать:
r 2 , ℓ. Как
а) тепловой поток (Q, Вт), рассеиваемый поверхностью
охлаждения трубы,
б) плотность теплового потока (q, Вт/м2), рассеиваемого
с 1м2 поверхности охлаждения?
48.Для цилиндрической стенки (трубы) с внутренним тепловыделением и
96
охлаждением только по внутренней поверхности дано: qv, r1, r 2 , ℓ.
Как
рассчитать: а) тепловой поток (Q, Вт), рассеиваемый поверхностью охлаждения трубы, б) плотность теплового потока (q, Вт/м2), рассеиваемого с 1 м2
поверхности охлаждения?
КОНТРОЛЬНАЯ РАБОТА №3
ЗАДАНИЕ № 1 (к. р. № 3)
Расчет теплоотдачи при естественной конвекции жидкости
Задание № 1 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Горячий горизонтальный трубопровод находится на открытом воздухе.
Рассчитать линейную плотность теплового потока (qℓ, Вт/м), передаваемого с
поверхности трубы к спокойному воздуху. Учесть теплоотдачу излучением.
Степень черноты поверхности принять εс=0,95.
Наружный диаметр трубы (d), температура наружной поверхности (tс) и
температура воздуха (tж) даны в табл. 1 по вариантам.
Таблица 1
№ варианта
1
160
6
180
11
200
16
220
21
240
d, мм
tс,°C
80
90
70
85
75
20
10
15
5
0
tж, °с
Примечание. Таблица теплофизических свойств воздуха дана в учебнике [4]
на с.402-403.
Задача № 2
Рассчитать тепловой поток (Q, Вт), передаваемый от нагретой вертикальной
трубы к спокойному окружающему воздуху с температурой tЖ=10°С. Наружный
диаметр трубы d=160 мм, температура поверхности трубы tс=90°С. Длина
трубы (ℓ) дана в табл.2 по вариантам.
Учесть теплоотдачу излучением от наружной поверхности трубы. Степень
черноты поверхности принять εс=0,95.
97
Таблица 2
№ варианта
2
7
12
17
22
ℓ, м
0,3
0,45
2
5
6
Примечание. Таблица теплофизических свойств воздуха дана в учебнике [4]
нас.402-403.
Задача № 3
Рассчитать тепловой поток (Q, Вт), передаваемый в окружающую среду от
плоской круглой горизонтальной крышки нагревательного прибора. Диаметр
крышки d=0,5м.
Учесть теплоотдачу излучением от поверхности крышки, степень черноты
принять εс=0,9.
Температура поверхности крышки (t с ) и температура воздуха (tж)даны в
табл. 3 по вариантам.
Таблица 3
№ варианта
3
8
13
18
23
t с , °С
60
65
70
75
80
t ж 1 , °С
10
15
20
25
30
Примечание.
Таблица теплофизических свойств воздуха дана в учебнике [4]
'жъ *"
на с.402-403.
Задача № 4
Через плоскую прослойку теплоносителя передается теплота от поверхности
с температурой t 1 к поверхности с температурой t2. Толщина прослойки
δ=100мм.
Рассчитать плотность теплового потока (q, Вт/м2). Теплоноситель, температуры поверхностей t 1 и t2 даны в табл.4 по вариантам.
Для воздушной прослойки учесть лучистый теплообмен между поверхностями, приняв, что расстояние между ними мало по сравнению с их размерами.
Степени черноты поверхностей ε 1 =0,85, ε2=0,55.
98
Таблица 4
№ варианта
Теплоноситель
4
Воздух
9
14
19
24
Масло
Вода Трансформаторное Масло МК
МС-20
масло
100
90
70
80
60
t 1 , °C
t2, °C
30
70
60
60
40
Примечание. Таблицы теплофизических свойств воздуха, воды и транс-
форматорного масла имеются в учебнике [4] на с.402-404. Таблицы для масел
МС-20 и МК даны в ПРИЛОЖЕНИИ учебного пособия [7] табл.4 и табл.5.
Задача № 5
Труба
горячего
воздуховода
наружным
диаметром
d 1 =160мм
для
уменьшения теплопотерь помещена в цилиндрический кожух внутренним
диаметром d 2 =200 мм. Между трубой и кожухом находится спокойный воздух.
Температура наружной поверхности воздуховода t 1 и температура внутренней
поверхности кожуха t 2 даны в табл. 5 по вариантам.
Рассчитать теплопотери через цилиндрическую прослойку воздуха для 1м
длины воздуховода (qℓ, Вт/м). Учесть теплообмен излучением между поверхностями воздуховода и кожуха, приняв степени черноты ε 1 =0,94,
ε 2 =0,532.
Таблица 5
варианта
5
10
15
20
25
t 1 , °С
90
100
110
120
130
t2, °C
30
40
30
40
50
Примечание. Таблица теплофизических свойств воздуха дана в учебнике [4]
на с.402-403.
99
ЗАДАНИЕ№ 2 (к. р. № 3)
Расчет теплоотдачи при вынужденной конвекции жидкости
Задание № 2 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Труба длиной ℓ наружным диаметром d, с температурой на наружной
поверхности t с омывается продольным потоком теплоносителя со средней
температурой t ж и скоростью w.
Рассчитать конвективную теплоотдачу (Q, Вт) между наружной поверхностью трубы и теплоносителем. Исходные данные для расчета приведены в
табл. 1 по вариантам.
Таблица 1
№ варианта
1
Теплоноситель
Воздух
w, м/с
tc,°C
t ж ,°C
15
60
10
Дымовые
газы
10
100
600
ℓ, м
d, мм
3
38
4
40
6
11
16
0,5
50
60
Трансформаторное масло
0,2
80
20
5
42
1,5
20
Вода
21
Масло МК
0,1
60
30
2
18
Примечание. Таблицы теплофизических свойств воздуха, дымовых газов,
воды и трансформаторного масла имеются в учебнике [4] на с.402-404. Таблица
для масла МК дана в ПРИЛОЖЕНИИ учебного пособия [7], табл.5.
Задача № 2
Труба длиной ℓ наружным диаметром d, с температурой на наружной
поверхности t с омывается поперечным потоком теплоносителя со средней
температурой t ж и скоростью w.
Рассчитать конвективную теплоотдачу (Q, Вт) между наружной поверхностью трубы и теплоносителем.
Исходные данные для расчета приведены в табл. 2 по вариантам.
100
Таблица 2
№ варианта
2
Теплоноситель
Воздух
w, М/С
tc, °С
15
60
7
Дымовые
газы
10
100
t ж , °С
ℓ, м
10
3
d, мм
38
12
2
50
17
Трансформаторное масло
0,2
80
600
4
60
5
20
1,5
30
2
40
100
20
36
Вода
22
Масло МК
0,5
60
Примечание. Таблицы теплофизических свойств воздуха, дымовых газов, воды
и трансформаторного масла имеются в учебнике [4] на с.402-404. Таблица для
масла МК дана в ПРИЛОЖЕНИИ учебного пособия [7], табл.5.
Задача № 3
По трубе с внутренним диаметром d длиной ℓ= 5 м со скоростью w течет
теплоноситель, имеющий среднюю температуру t ж . Температура внутренней
поверхности трубы t с .
Рассчитать конвективную теплоотдачу (Q, Вт) между внутренней поверхностью трубы и теплоносителем.
Исходные данные для расчета приведены в табл. 3 по вариантам.
Таблица 3
№ варианта
3
8
13
18
23
Дымовые
ТрансформаТеплоноситель Воздух
Вода
Масло МК
газы
торное масло
d, мм
40
38
36
28
26
w, м/с
15
10
0,5
0,1
0,5
80
400
70
30
40
tж
tc, °C
150
100
75
40
30
Примечание. Таблицы теплофизических свойств воздуха, дымовых газов,
воды и трансформаторного масла имеются в учебнике [4] на с.402-404. Таблица
для масла МК дана в ПРИЛОЖЕНИИ учебного пособия [7], табл. 5.
101
Задача № 4
Трубный пучок с шахматным расположением стальных труб омывается
поперечным потоком воздуха. Скорость (w) и средняя температура воздуха
(t ж ), наружный диаметр труб (d) и температура наружной поверхности труб (t с )
даны в табл. 4 по вариантам. Продольный и поперечный шаги трубного пучка
s 1 = s2 = 2d.
Определить средние коэффициенты теплоотдачи ( ) и линейные плотности
конвективного теплового потока (qℓ, Вт/м) для труб 1, 2 и 3 рядов трубного
пучка, если в каждом ряду находится 8 труб.
Таблица 4
№ варианта
4
9
14
19
24
d, мм
30
32
38
40
42
w, м/с
10
12
14
15
16
120
140
160
180
200
tж
tc,°C
400
450
500
550
600
Примечание. Таблица теплофизических свойств воздуха дана в учебнике [4] на
с.402-403.
Задача № 5
Трубный пучок с коридорным расположением стальных труб омывается
поперечным потоком дымовых газов. Наружный диаметр труб (d), скорость (w)
и средняя температура дымовых газов (tж) даны в табл. 5 по вариантам.
Температура наружной поверхности труб tc=90°C. Продольный и поперечный
шаги трубного пучка s1=s2=2d. Число рядов п=10, число труб в ряду т=20,
длина труб ℓ = 6м.
Определить средний коэффициент теплоотдачи для коридорного пучка
( пучка) и конвективный тепловой поток (Q, Вт), передаваемый от газов к поверхности труб.
Таблица 5
№ варианта
5
10
15
20
25
d, мм
30
32
38
40
42
w, м/с
10
12
14
15
16
t ж ,°С
400
450
500
550
600
1 ж, \_Примечание.
Таблица теплофизических свойств дымовых газов дана в
учебнике [4] на с.404.
102
ЗАДАНИЕ №3 (к.р.№3)
Расчет теплоотдачи при фазовых превращениях
Задание № 3 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Сухой насыщенный пар с давлением р конденсируется на наружной поверхности вертикальной трубы. Температура поверхности (tс), длина (ℓ) и
диаметр (d) трубы, а также давление пара (р) приведены в табл. 1 по вариантам.
Рассчитать средний коэффициент теплоотдачи ( ) и количество конденсата, стекающего с трубы за 1 час (G, кг/ч).
Таблица 1
№ варианта
р, бар
d, мм
ℓ, м
tc, 0С
1
0,0424
20
2
20
6
0,0737
24
2,5
30
11
0,123
26
3
40
16
0,701
22
4,5
75
21
1,013
28
5
90
Примечание. Таблицы теплофизических свойств воды и водяного пара на
линии насыщения даны в ПРИЛОЖЕНИИ учебного пособия [7], табл.6 и 7
Задача № 2
Сухой насыщенный пар с давлением р конденсируется на наружной поверхности горизонтальной трубы. Температура поверхности (tc), длина (ℓ) и
диаметр (d) трубы, а также давление пара (р) приведены в табл.2 по вариантам.
Рассчитать средний коэффициент теплоотдачи ( )и количество конденсата,
стекающего с трубы за 1 час (G, кг/ч).
Таблица 2
№ Варианта
2
7
12
17
22
р, бар
0,0424
0,0737
0,123
0,701
13
d, мм
20
24
26
22
28
ℓ, м
2
2,5
3
4,5
5
tc, 0C
20
30
40
75
90
Примечание. Таблицы теплофизических свойств воды и водяного пара на
линии насыщения даны в ПРИЛОЖЕНИИ учебного пособия [7], табл.6 и 7.
103
Задача № 3
Сухой насыщенный пар, движущийся со скоростью wn= 10м/с, конденсируется на наружной поверхности горизонтальной трубы. Температура наружной поверхности трубы (tc), длина ее (ℓ) и диаметр (d), а также давление
пара (р) приведены в табл.3 по вариантам.
Таблица 3
№ варианта
р, бар
d, мм
ℓ, м
3
0,0424
20
2
8
0,0737
24
2,5
13
0,123
26
3
18
0,701
22
4,5
23
1,013
28
5
tc, °C
20
30
40
75
90
Примечание. Таблицы теплофизических свойств воды и водяного пара на
линии насыщения даны в ПРИЛОЖЕНИИ учебного пособия [7], табл.6 и 7.
Задача № 4
При пузырьковом кипении воды в условиях естественной конвекции известны давление воды (р) и плотность теплового потока, подводимого к поверхности нагрева (qc).
Рассчитать коэффициент теплоотдачи (а), используя:
а)
уравнение Кружилина,
б)
эмпирическую формулу a=f (p, qc).
Оценить (в процентах) отклонение полученных результатов.
Рассчитать температуру на поверхности нагрева (tс) и количество испаряющейся жидкости с 1м 2 поверхности нагрева за 1час (G, кг/ч). Исходные
данные приведены в табл.4 по вариантам.
Таблица 4
№ варианта
4
9
14
19
24
р, бар
1,013
1,985
4,76
10,03
15,55
2
4
4
4
4
qc, Вт/м
210
310
510
710
9104
Примечание. Таблицы теплофизических свойств воды и водяного пара на
линии насыщения даны в ПРИЛОЖЕНИИ учебного пособия [7], табл.6 и 7.
104
Задача № 5
Кипящая вода движется по трубе со скоростью w. Температура внутренней поверхности трубы (tc) давление (р), скорость воды (w), внутренний
диаметр трубы (d) приведены в табл.5 по вариантам.
Рассчитать средний коэффициент теплоотдачи ( ) от поверхности трубы
к кипящей воде.
Таблица 5
№ варианта
5
10
15
20
25
p, бар
1,013
1,985
4,76
10,03
12,55
d, мм
30
32
36
40
42
w, м/с
1
0,5
0,8
0,3
0,1
0
tc, С
110
130
155
185
200
Примечание. Таблицы теплофизических свойств воды и водяного пара на
линии насыщения даны в ПРИЛОЖЕНИИ учебного пособия [7] табл.6 и 7.
ЗАДАНИЕ № 4 (к. р. № 3)
Теплообмен излучением
Задание № 4 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
Рассчитать плотность потока излучения (q, Вт/м2) между двумя плоскими
параллельными поверхностями с температурами t1 и t2, степенями черноты ε1 и
ε2. Расстояние между поверхностями мало по сравнению с их размерами.
Как изменится плотность лучистого теплового потока (q', Вт/м2), если между
двумя поверхностями установить экран со степенью черноты εэ?
Исходные данные для расчета приведены в табл. 1 по вариантам.
Таблица 2
№ варианта
1
6
11
16
21
t1,°C
150
170
190
210
230
t2,°C
57
67
87
60
70
ε1
0,4
0,5
0,6
0,4
0,5
ε2
0,8
0,9
0,85
0,9
0,95
ε3
ОД
0,2
0,3
0,2
0,15
105
Задача № 2
Рассчитать потерю тепла излучением с 1м длины горячей трубы (q, Вт/м),
расположенной на открытом воздухе.
Наружный диаметр трубы (d), температура наружной поверхности (tс),
температура воздуха (tж) даны в табл.2 по вариантам. Степень черноты поверхности трубы εс=0,9.
Как изменится потеря тепла излучением (q', Вт/м), если трубу заключить в
кожух из жести со степенью черноты εк=0,4?
Размеры и форма кожуха даны в табл.2.
Таблица 2
№
варианта
2
7
12
17
22
d, мм
200
240
300
350
400
tc, °C
70
75
60
65
60
tж,°C
20
15
5
25
30
Форма и Круглого Квадратного Прямоуголь- Квадратного Прямоугольразмеры сечения
сечения
ного сечения со сечения со ного сечения
кожуха в dK=260 со стороной
сторонами
стороной
со сторонами
мм
а = 300
a×в = 340×360
а = 410
a×в=400×460
Задача № 3
Рассчитать теплообмен излучением между дымовыми газами и внутренней
поверхностью дымовой трубы для 1м длины трубы (q, Вт/м).
Степень черноты поверхности трубы εс=0,95.
Дымовые газы содержат 11% водяных паров (Н2О) и 13% углекислого газа
(СО2) по объему. Общее давление газов р0=1ат.
Средняя температура газов (tг), диаметр (d) и температура внутренней
поверхности трубы (tc) даны в табл.3 по вариантам.
106
Таблица 3
№ варианта
d, мм
tc, °С
tг , oС
3
800
400
600
8
700
300
500
13
600
350
550
18
650
200
400
23
750
250
450
Задача № 4
Рассчитать теплообмен излучением между дымовыми газами и внутренней
поверхностью газохода для 1 м длины его (q, Вт/м). Канал газохода в поперечном
сечении имеет форму прямоугольника со сторонами axe. Степень черноты
поверхности газохода εс=0,95.
Дымовые газы содержат 15% водяных паров (Н2O) и 13% углекислого газа
(СО2) по объему. Общее давление газов ро=1 ат.
Размеры газохода, температура его внутренней поверхности (tc), средняя
температура газов (tг) даны в табл.4 по вариантам.
Таблица 4
№ варианта
4
9
14
19
24
a×в, м2
0,5×1,5
0,7×1,5
0,6×1,2
0,8×1,4
0,9×1,7
tс, оС
300
400
600
650
700
tг, ОС
500
600
850
900
950
Задача № 5
Рассчитать плотность потока тепла (q, Вт/м2), передаваемого излучением, от
дымовых газов к поверхности труб пароперегревателя парового котла.
Трубы расположены в шахматном порядке, наружный диаметр труб d,
продольный и поперечный шаги s1=s2=2d. Дымовые газы содержат 4% водяных
паров (Н2О) и 10% углекислого газа (СО2) по объему. Общее давление газов рo=1ат.
Степень черноты поверхности труб εс=0,8.
Наружный диаметр труб (d), температура их поверхности (tc), средняя температура
дымовых газов(«г) даны в табл.5 по вариантам
107
Таблица 5
№ варианта
5
10
15
20
25
d, мм
38
40
42
44
46
t г , °С
1100
1000
900
950
1050
tc, °C
700
600
500
550
650
ЗАДАНИЕ № 5 (к. р. № 3)
Теплообменные аппараты
Задание № 5 содержит 5 задач для 25 вариантов. Каждый студент решает
одну задачу в соответствии со своим вариантом.
Задача № 1
В кожухотрубном пароводяном теплообменнике производится подогрев
воды, движущейся в трубах, за счет тепла конденсации сухого насыщенного
пара на поверхности труб.
Давление воды р=1 бар, температуры воды на входе в теплообменник (t2'),
на выходе (t2"), расход воды (GB) и давление конденсирующегося пара (р) даны
в табл.1 по вариантам. Конденсат на выходе из теплообменника имеет
температуру насыщения (ts) при давлении р.
Принять средний коэффициент теплопередачи от пара к воде через стенку
трубы К=3000 Вт/м2 -К. Потерями тепла в окружающую среду пренебречь.
Рассчитать расход пара (GП, кг/с) и площадь поверхности нагрева теплообменника (F, м2).
Представить графики изменения температуры теплоносителей вдоль
поверхности нагрева по схемам прямотока и противотока. Как влияет схема
движения теплоносителей (прямоток или противоток) на результаты расчета?
108
Таблица 1
№ варианта
1
6
11
16
21
t2', °C
20
25
30
35
40
t2",оC
70
75
80
85
90
GB , кг/ч
105
5·104
104
2-104
7·104
р, бар
1,1
1,2
1,3
1,4
1,5
Задача № 2
В трубчатом воздухоподогревателе воздух нагревается за счет тепла
дымовых газов. Дымовые газы движутся по трубам, поперечный поток воздуха
омывает трубный пучок.
Расход воздуха (GB), температуры воздуха на входе (t2') и на выходе (t2"),
расход дымовых газов (Gг), температура дымовых газов на входе (t1') даны в
табл.2 по вариантам.
Принять коэффициент теплопередачи от дымовых газов к воздуху через
стенку трубы К=30 Вт/м2 ·К. Потерями тепла в окружающую среду пренебречь.
Рассчитать температуру дымовых газов на выходе (t1") и площадь поверхности нагрева воздухоподогревателя (F, м2).
Таблица 2
№ варианта
2
7
12
17
22
GB, кг/с
21
25
30
35
40
t2', °С
30
25
20
35
15
t2'', °C
250
240
270
290
250
Gr, кг/с
20
30
40
45
42
t1', oC
400
370
390
450
380
Задача № 3
В противоточном теплообменнике типа "труба в трубе" горячее трансформаторное масло охлаждается водой. Трансформаторное масло движется по
внутренней латунной трубе с диаметром d2/d1=14/12 мм. Вода движется по
кольцевому зазору. Внутренний диаметр наружной трубы d3=22 мм. Скорость
109
масла (w1) и температуры его на входе (t1') и на выходе (t1'') из теплообменника,
а также скорость воды (w2) и температура воды на входе в теплообменник (t2')
даны в табл.3 по вариантам.
Принять средний коэффициент теплопередачи от масла к воде через стенку
трубы К=230 Вт/м -К. Потерями тепла в окружающую среду пренебречь.
Определить температуру воды на выходе из теплообменника (t2"), площадь
поверхности теплообмена (F, м2) и общую длину теплообменной поверхности
(ℓ м).
Представить график изменения температуры теплоносителей вдоль поверхности
теплообмена.
Таблица 3
№ варианта
3
8
13
18
23
w1, м/с
4
3
3,5
2
2,5
t1', °С
100
110
90
80
120
t1", °C
60
70
50
40
70
t2', °С
20
10
15
25
20
w2 , м/с
2,5
2
2,2
1,7
1,9
Задача № 4
В трубчатом испарителе воды горячим теплоносителем является технологический сухой насыщенный пар, подаваемый в межтрубное пространство
при давлении р1. За счет тепла конденсации пара в трубах кипит и испаряется
вода при давлении р2. На вход испарителя подается сухой насыщенный пар при
давлении p1 и кипящая вода при давлении р2, на выходе из испарителя конденсат с температурой насыщения (ts1) при давлении p1 и сухой насыщенный
пар с температурой (ts2) при давлении р2. Давления p1, p2 и расход воды (G2) даны
в табл.4 по вариантам.
Принять средний коэффициент теплопередачи от пара к воде через стенку
трубы К=2200 Вт/м2 -К. Потерями тепла в окружающую среду пренебречь.
Определить расход пара (G1, кг/ч) и площадь поверхности теплообмена
испарителя (F, м2).
110
Представить график изменения температур теплоносителей вдоль поверхности теплообмена.
Таблица 4
№ варианта
p1, бар
р2, бар
G2, кг/ч
4
2
1
1000
9
3
1,5
800
14
3,6
2
1200
19
4
2,2
1300
24
5
3
900
Задача № 5
Трубчатый испаритель воды обогревается дымовыми газами. Давление воды
р, температура воды на входе в испаритель равна температуре насыщения (ts)
при давлении р, на выходе - сухой насыщенный пар.
Давление воды (р), температура дымовых газов на входе (t1') и на выходе из
испарителя (t1''), а также расход газов (G1) даны в табл.5 по вариантам.
Принять средний коэффициент теплопередачи от пара к воде через стенку
трубы К=70 Вт/м2 -К. Потерями тепла в окружающую среду пренебречь.
Определить расход воды (G2, кг/с) и площадь поверхности теплообмена
испарителя (F, м2).
Представить график изменения температур теплоносителей вдоль поверхности теплообмена.
Таблица 5
№ варианта
5
10
15
20
25
p1, бар
2,7
3,4
4,4
5,6
6,5
t1’, °С
600
650
700
750
800
t1", °C
320
340
380
420
460
G1, кг/с
38
40
43
45
50
111
ЗАДАНИЕ №6 (к. р.№3)
Расчет теплопередачи со сложным теплообменом на поверхностях
Рекомендуется разобраться с данной темой на примере задач № 1 и № 2. В
учебном пособии [7] приводится метод решения задач со сложным теплообменом на поверхностях стенки, когда необходимо учитывать одновременную
передачу теплоты двумя или тремя способами (теплопроводностью, конвекцией,
излучением).
Решение данных задач необязательно, но желательно в целях повышения
уровня знаний по данной дисциплине.
Задача № 1
Рассчитать теплопотери (Q, Вт/м) через стенку горячей горизонтальной
трубы в окружающую среду (к спокойному воздуху).
Диаметр трубы d2/d1=150/140 мм, коэффициент теплопроводности стали λс=50
Вт/м-К, температура на внутренней поверхности трубы t1=90°C, степень
черноты наружной поверхности трубы εc=0,9, температура воздуха tЖ = 10°С.
Задача № 2
Рассчитать теплопотери (Q, Вт/м) из помещения в окружающую среду через
оконный проем с двойным стеклом (рис.3.1).
Рис. 3.1
Температуры на поверхностях стекла: t1=10°C, t4=-20°C; толщина стекла
δс=3мм, ширина воздушного зазора между стеклами δ=15см. Площадь
поверхности оконного проема F=2×1,5м2. Степень черноты стекла εс=0,937,
коэффициент теплопроводности стекла λc=0,74 Вт/м-К.
112
КОНТРОЛЬНЫЕ ВОПРОСЫ (к.р. № 3)
1. Сформулируйте
практическое
условия
подобия
физических
применение теории подобия и
процессов.
моделирования
Каково
процессов
конвективного теплообмена?
2. Дайте краткую характеристику теплофизических свойств теплоносителей:
коэффициентов
динамической
и
кинематической
вязкостей,
коэффициента сжимаемости, температурного коэффициента объемного расширения.
3. Запишите число Грасгофа, поясните его физический смысл. Назовите все
величины, входящие в число Грасгофа, укажите их размерность.
4. Запишите числа Рейнольдса и Прандтля, дайте их характеристику.
Поясните физический смысл и размерность величин, входящих в эти числа.
5. Приведите примеры определяемых и определяющих чисел подобия.
Дайте понятие определяющей температуры и определяющего размера в
уравнениях подобия.
6. Приведите уравнение подобия для расчета среднего коэффициента
теплоотдачи при вынужденном турбулентном течении жидкости в трубе.
Проанализируйте зависимость коэффициента теплоотдачи от диаметра трубы
(d), вязкости (v), скорости (w), теплопроводности (λ), теплоемкости (с) и
плотности (ρ) жидкости.
7. Что характеризует коэффициент
t
Prж
Рrc
0, 25
? Рассчитайте коэффициент
εt для следующих случаев:
а)нагрев воды с температурой tЖ=60 °С у поверхности с температурой
tc=80 °C;
б)охлаждение воды с температурой tЖ=80 °С у поверхности с температурой
tc=60 oС;
в)нагрев и охлаждение воздуха при тех же условиях.
Сделайте выводы. Таблицы теплофизических свойств воды и воздуха
имеются в учебнике [4] на с. 402-403.
113
8. Ниже перечислены величины, влияющие на коэффициенты
теплоотдачи:
λ[Вт/м -К], ℓ [м], ζ=tc-tж [oС], g[м/c2], β[1/K], v[м2/c], а[м2/с], с[Дж/кг-К],
ρ[кг/м3], w[м/c].
Укажите величины, влияющие на теплоотдачу при естественной конвекции.
9. Ниже перечислены величины, влияющие на коэффициенты теплоотдачи:
λ[Вт/м-К], ℓ [м], ζ=tc-tж [oС], g[м/c2], β [1/K], v[м2/c], а[м2/с], с[Дж/кг-К],
р[кг/м3], w[м/c].
Укажите величины, влияющие на теплоотдачу при смывании поверхности
вынужденным продольным потоком жидкости.
10.Ниже перечислены величины, влияющие на коэффициент теплоотдачи:
λ[Вт/м-К],
ℓ [м],
d[м],
ζ=tc-tж [oС],
g[м/c2],
l/к],
v[M2/c],
а[м2/с],
с[Дж/кг-К], р[кг/м3], w[м/c].
Укажите величины, влияющие на теплоотдачу при вынужденном турбулентном течении жидкости в трубах.
11.Какие режимы могут иметь место при вынужденном течении жидкости в трубах? Как определить режим течения?
12.Какие режимы течения в пограничном слое могут иметь место при
естественной конвекции жидкости около вертикальной поверхности в большом
объеме? Как определить режим течения?
13.Укажите
величины,
характеризующие
теплофизические
свойства
жидкостей, которые влияют на коэффициент теплоотдачи при пузырьковом
кипении жидкости в условиях естественной конвекции. Приведите их раз
мерность.
14.Укажите
величины,
характеризующие
теплофизические
свойства
пара или пленки конденсата, которые влияют на коэффициент теплоотдачи
при пленочной конденсации неподвижного пара на вертикальной поверхности.
Приведите их размерность.
15.Приведите
кривую
кипения
при
паровом
обогреве
и
дайте
характеристику ее отдельных участков.
16.Приведите кривую кипения при электрическом обогреве. При каком
114
условии возможен пережог поверхности нагрева в теплообменниках с
кипением?
Перечислите микро- и макрохарактеристики, влияющие на интенсивность
пузырькового
кипения
жидкости.
Как
зависит
коэффициент
тепло
отдачи от этих характеристик?
18. Как влияет скорость вынужденного течения жидкости в испарительных трубах теплообменников на процесс кипения?
19. При каких условиях наблюдается
а) пленочная конденсация пара;
б) капельная конденсация пара?
Сравните их по коэффициенту теплоотдачи. Какой тип конденсации
имеет место в промышленных конденсаторах?
20.Укажите
особенности
расчета
коэффициента
теплоотдачи
при
пленочной конденсации перегретого или мокрого пара по сравнению с
конденсацией сухого насыщенного пара.
21.Как влияет на коэффициент теплоотдачи при конденсации пара
а) состояние поверхности (гладкая, шероховатая),
б) содержание воздуха в паре?
22.Ниже
записаны
два
уравнения
теплового
баланса:
a) G ·r = a (ts - tc) F,
6)G ·r = a (tc- ts) F.
Для каких процессов записаны уравнения? Поясните их смысл. Укажите
размерность всех величин.
23.Для процесса пленочной конденсации неподвижного сухого насыщенного пара на горизонтальной трубе проанализируйте:
а)зависимость коэффициента теплоотдачи от разности температур (ts-tc),
б)зависимость теплового потока (q, Вт/м2 ) от разности температур (ts-tc).
Сделайте выводы.
24.Какие режимы течения стекающей пленки конденсата могут иметь
место при пленочной конденсации неподвижного сухого насыщенного пара
на вертикальной поверхности? Как определить режим течения и какими
115
уравнениями воспользоваться для расчета среднего коэффициента теплоотдачи?
25.Дайте понятие степени черноты твердого тела. Как рассчитать по
ток собственного излучения тела с известной температурой Т и площадью
излучающей поверхности F?
26.Известно, что уменьшить передачу тепла излучением между телами
можно, если поставить между ними экран.
Как влияет расстояние от излучающей поверхности до экрана на лучистый поток для системы тел:
а) две параллельные плоские поверхности,
б) труба в цилиндрическом кожухе?
27.Назовите, какой имеет спектр излучения (сплошной или дискретный)
и от каких факторов зависит излучательная способность твердых тел.
б) излучающих газов.
28.Приведите уравнение для расчета теплообмена излучением между
двумя телами, произвольно расположенными в пространстве. Дайте понятие
угловых коэффициентов
1, 2 ,
2 ,1 .
В каких пределах изменяются угловые
коэффициенты и от чего они зависят?
29.Дайте понятие коэффициентов поглощения, отражения и пропускания.
Назовите пределы их изменения. Запишите связь между ними.
30.Какие газы излучают и поглощают лучистую энергию? Как определяется степень черноты излучающих газов?
31.Запишите связи между потоками излучения:
а) падающим, поглощенным, отраженным, пропущенным;
б)эффективным, собственным, отраженным;
в) результирующим, собственным, поглощенным;
г) результирующим, падающим, эффективным.
32.Как рассчитывается длина пути луча для замкнутых объемов излучающего газа и как она используется в расчетах теплообмена излучением
между газом и оболочкой?
116
33.Дайте понятие для излучающего газа:
а)степени черноты εг,
б)предельной степени черноты
Г
.
Как определяются Г и Г ?
34.Сравните излучательную способность углекислого газа (СО2) и водяных
паров (Н2О). Сделайте выводы.
35.Дайте формулировку и математическую запись закона Стефана Больцмана. Приведите формулы для расчета собственного излучения
а)твердых тел,
б) излучающих газов.
36.Какой закон теплового излучения устанавливает равенство между
степенью черноты тела (ε) и коэффициентом поглощения (А)? Приведите
доказательство равенства ε=А.
37.Запишите уравнение теплового баланса для расчета теплообменников.
Дайте понятие расходных теплоемкостей теплоносителей. Какова связь
между расходными теплоемкостями и изменением температур теплоносителей?
38.Чему равны расходные теплоемкости теплоносителей для испарителя,
в котором происходит испарение холодного теплоносителя за счет тепла
конденсации горячего теплоносителя? Приведите график изменения температур вдоль поверхности нагрева такого испарителя.
39.Какова цель конструкторского расчета теплообменника? Как рассчитывается коэффициент теплопередачи?
40. Какова роль поверочного расчета теплообменников? Приведите
уравнения для расчета конечных температур теплоносителей t1", t2".
41. Сравните
по
эффективности
теплообмена
схемы
движения
теплоносителей: прямоток и противоток. В каких случаях прямоток и
противоток равнозначны? Приведите примеры таких теплообменников.
42. Перечислите виды теплообменников. К каким видам можно
отнести:
конденсатор,
паровой
котел,
градирню,
подогреватель
питательной воды поверхностного типа, электрокотел, ядерный реактор?
43. Приведите графики изменения температуры теплоносителей для
117
следующих соотношений между расходными теплоносителями:
а) с,>с2;
б) c 1 >>с 2 ;
с1 ∞ .
44.Приведите графики изменения температуры теплоносителей для
следующих соотношений между расходными теплоносителями:
а) с2>с1;
б) c 2 >>с 1 ;
с2 ∞ .
45. Запишите уравнение теплового баланса теплообменника с учетом
потерь тепла в окружающую среду.
46. Как вычислить средний температурный напор для прямотока,
противотока, перекрестного тока? Приведите примеры теплообменников с
указанными схемами движения теплоносителей.
47. В каком случае среднелогарифмический температурный напор
можно заменить среднеарифметическим? Приведите график изменения
температур теплоносителей вдоль поверхности теплообмена и поясните
ответы, используя график.
48. Какие теплообменники называются рекуперативными? Приведите
примеры таких теплообменников.
5. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
5.1. Литература обязательная
1. Кириллин В.А., Сычев В.В, Шейндлин А.Е. Техническая
термодинамика. -М.: Энергоатомиздат, 1983.
2. Ривкин
С.Л.
Термодинамические
свойства
газов.
-М.: Энергоиздат, 1987.
3. Вукалович М.П., Ривкин С.Л., Александров А.А. Таблицы
теплофизических свойств воды и водяного пара. - М.: Издательство
стандартов, 1969.
4. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. -М.:
Энергоиздат, 1981.
5. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче
-М.: Энергия, 1980.
6. Сборник задач по технической термодинамике. / Андрианова Т.Н. и
д р. -М.: Энергоиздат, 1981.
118