Решение задач типа С2 при подготовке к ЕГЭ. №1.В
реклама
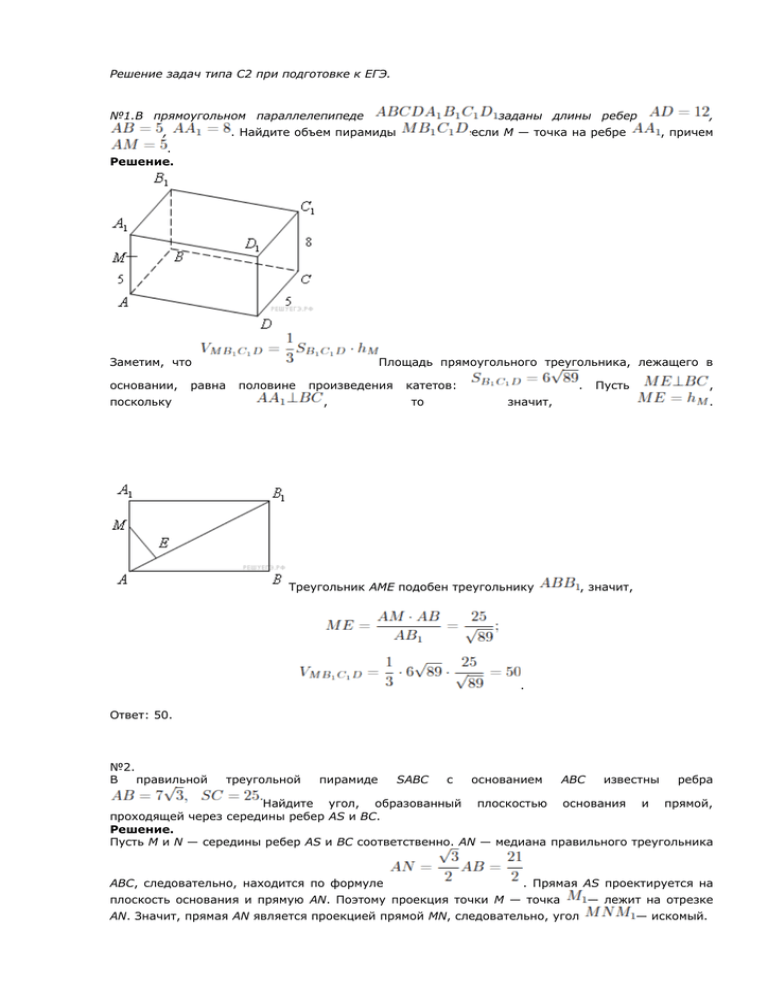
Решение задач типа С2 при подготовке к ЕГЭ. №1.В прямоугольном параллелепипеде , заданы длины ребер . Найдите объем пирамиды если M — точка на ребре , , причем . Решение. Заметим, что основании, равна Площадь прямоугольного треугольника, лежащего в половине поскольку произведения , катетов: то . Пусть , значит, . Треугольник AME подобен треугольнику , значит, . Ответ: 50. №2. В правильной треугольной пирамиде SABC с основанием ABC известны ребра Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC. Решение. Пусть M и N — середины ребер AS и BC соответственно. AN — медиана правильного треугольника ABC, следовательно, находится по формуле . Прямая AS проектируется на плоскость основания и прямую AN. Поэтому проекция точки M — точка AN. Значит, прямая AN является проекцией прямой MN, следовательно, угол — лежит на отрезке — искомый. где O — центр основания, значит, — средняя линия треугольника ASO потому — Тогда находим: AO. и Из прямоугольного треугольника Значит, искомый Из прямоугольного треугольника находим: угол равен Ответ: №3. В правильной треугольной SABC пирамиде с основанием ABC известны ребра . Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC. Решение. Пусть N — середина ребра BC, а M — середина AS. Прямая AS проецируется на плоскость основания в прямую AN. Поэтому проекция точки M — точка прямая AN является проекцией прямой AM, следовательно, угол , где O — центр основания, — лежит на отрезке AN. Значит, — искомый. Поскольку — средняя линяя треугольника SAO. Тогда Кроме того, Из прямоугольного треугольника находим: . Ответ: . №4. В прямоугольном параллелепипеде . Найдите угол между плоскостями ABC и известны ребра: , , . Решение. Плоскости ABC и о трех перпендикулярах ABC и — это угол имеют общую прямую BD. Проведем перпендикуляр AH к BD. По теореме . Значит, угол двугранного угла, образованного плоскостями . Из прямоугольного треугольника BAD находим: . Из прямоугольного треугольника находим: . Значит, искомый Ответ: угол равен . . №5. В кубе Решение. найдите косинус угла между плоскостями Пусть точка O — центр куба, а M — середина треугольника , поэтому . . стороны треугольника треугольника . Из . , а MO — средняя линия Треугольник , следовательно, искомый угол равен углу Найдем и — равносторонний, . треугольника , находим из находим . поскольку O — середина диагонали косинусов: , . Теперь применим к треугольнику теорему . Ответ: . №6. В правильном тетраэдре ABCD найдите угол между высотой тетраэдра DH и медианой BM боковой грани BCD. Решение. Пусть и MK — средняя линия треугольника CDH. Тогда следовательно, , значит, и, . Кроме того, . Далее имеем: ; ; ; Ответ: . . №7. В правильном тетраэдре ABCD найдите угол между медианой BM грани ABD и плоскостью BCD. Решение. Пусть, DN — высота грани BCD, O — центр треугольника BCD, MK — средняя линия треугольника ADO. Тогда искомый. , Кроме того, Далее имеем: , значит, и, следовательно, , откуда — . ; . Ответ: . №8. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между плоскостью SAD и плоскостью, проходящей через точку A перпендикулярно прямой BD. Решение. Пусть точка O — центр основания, а M — середина ребра AS. Поскольку и плоскость SAC перпендикулярна прямой BD. Это значит, что плоскость SAC и есть плоскость, проходящая через точку A перпендикулярно BD. Проведем отрезки MD и MO. Так как треугольник SAD правильный, треугольник ASO — равнобедренный, Найдем стороны треугольника OMD: Так как Следовательно, искомый угол равен углу OMD. . По теореме косинусов: . Отсюда . Ответ: . №9. В правильной шестиугольной призме все ребра которой равны 1 найдите расстояние от точки Bдо прямой Решение. Проведем отрезки BF и проекция . , поскольку образом искмое расстояние — длина отрезка Рассмотрим а на плоскость основания. По теореме о трех перпендикулярах треугольник . Он . BF — Таким . прямоугольный, По теореме Пифагора находим: . . Ответ: 2. №10. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD. Решение. Вместо прямой CD рассмотрим параллельную ей прямую BE. Искомый угол равен углу SBE. Треугольник SBE равносторонний, поскольку большая диагональ правильного шестиугольника вдвое больше Ответ: . его стороны: . Следовательно, Литература: Использован образовательный портал для подготовки к ЕГЭ. Решу ЕГЭ .



