У Е. С. Воробьёва*, Р. Р. Сафаров, Е. В. Гусева,...
реклама
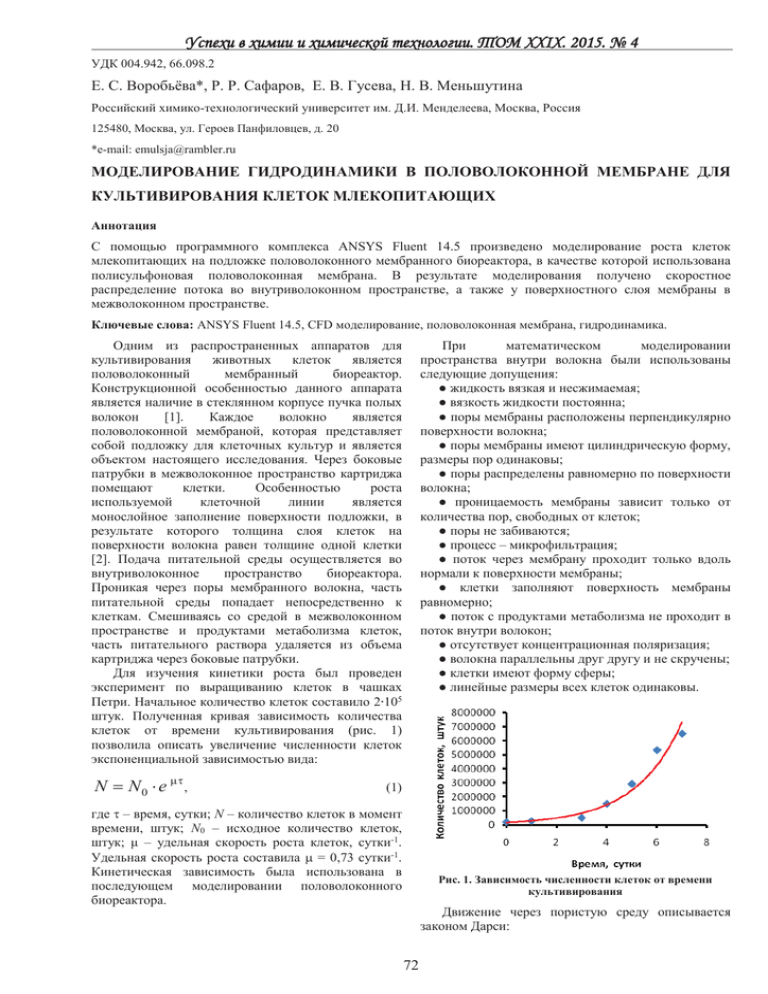
Успехи в химии и химической технологии. ТОМ XXIX. 2015. № 4 УДК 004.942, 66.098.2 Е. С. Воробьёва*, Р. Р. Сафаров, Е. В. Гусева, Н. В. Меньшутина Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия 125480, Москва, ул. Героев Панфиловцев, д. 20 *e-mail: emulsja@rambler.ru МОДЕЛИРОВАНИЕ ГИДРОДИНАМИКИ В ПОЛОВОЛОКОННОЙ МЕМБРАНЕ ДЛЯ КУЛЬТИВИРОВАНИЯ КЛЕТОК МЛЕКОПИТАЮЩИХ Аннотация С помощью программного комплекса ANSYS Fluent 14.5 произведено моделирование роста клеток млекопитающих на подложке половолоконного мембранного биореактора, в качестве которой использована полисульфоновая половолоконная мембрана. В результате моделирования получено скоростное распределение потока во внутриволоконном пространстве, а также у поверхностного слоя мембраны в межволоконном пространстве. Ключевые слова: ANSYS Fluent 14.5, CFD моделирование, половолоконная мембрана, гидродинамика. Одним из распространенных аппаратов для культивирования животных клеток является половолоконный мембранный биореактор. Конструкционной особенностью данного аппарата является наличие в стеклянном корпусе пучка полых волокон [1]. Каждое волокно является половолоконной мембраной, которая представляет собой подложку для клеточных культур и является объектом настоящего исследования. Через боковые патрубки в межволоконное пространство картриджа помещают клетки. Особенностью роста используемой клеточной линии является монослойное заполнение поверхности подложки, в результате которого толщина слоя клеток на поверхности волокна равен толщине одной клетки [2]. Подача питательной среды осуществляется во внутриволоконное пространство биореактора. Проникая через поры мембранного волокна, часть питательной среды попадает непосредственно к клеткам. Смешиваясь со средой в межволоконном пространстве и продуктами метаболизма клеток, часть питательного раствора удаляется из объема картриджа через боковые патрубки. Для изучения кинетики роста был проведен эксперимент по выращиванию клеток в чашках Петри. Начальное количество клеток составило 2ή105 штук. Полученная кривая зависимость количества клеток от времени культивирования (рис. 1) позволила описать увеличение численности клеток экспоненциальной зависимостью вида: N N 0 e PW , При математическом моделировании пространства внутри волокна были использованы следующие допущения: ● жидкость вязкая и несжимаемая; ● вязкость жидкости постоянна; ● поры мембраны расположены перпендикулярно поверхности волокна; ● поры мембраны имеют цилиндрическую форму, размеры пор одинаковы; ● поры распределены равномерно по поверхности волокна; ● проницаемость мембраны зависит только от количества пор, свободных от клеток; ● поры не забиваются; ● процесс – микрофильтрация; ● поток через мембрану проходит только вдоль нормали к поверхности мембраны; ● клетки заполняют поверхность мембраны равномерно; ● поток с продуктами метаболизма не проходит в поток внутри волокон; ● отсутствует концентрационная поляризация; ● волокна параллельны друг другу и не скручены; ● клетки имеют форму сферы; ● линейные размеры всех клеток одинаковы. (1) где W – время, сутки; N – количество клеток в момент времени, штук; N0 – исходное количество клеток, штук; μ – удельная скорость роста клеток, сутки-1. Удельная скорость роста составила P = 0,73 сутки-1. Кинетическая зависимость была использована в последующем моделировании половолоконного биореактора. Рис. 1. Зависимость численности клеток от времени культивирования Движение через пористую среду описывается законом Дарси: 72 Успехи в химии и химической технологии. ТОМ XXIX. 2015. № 4 μ& 䌛p = v , α распределение потока во внутриволоконном пространстве, а также у поверхностного слоя мембраны в межволоконном пространстве (рис. 3). С течением времени культивирования клетки будут заполнять поверхность волокна монослоем, уменьшая проницаемость мембраны на несколько порядков, поэтому на рисунке 2 продемонстрировано моделирование потока питательной среды через половолоконную мембрану для случаев максимальной проницаемости (отсутствие клеток) и на начальных стадиях образования монослоя клеток. Таким образом, проницаемость мембраны, рассчитанная по зависимостям (2)–(4) составила 81012 2 м . С учетом принятых допущений и рассчитанных параметров произведено моделирование движения потоков через половолоконную мембрану в программном комплексе ANSYS Fluent (рис. 2, 3). (2) где μ – динамическая вязкость; α – проницаемость пористого тела. В данном случае поры мембраны можно считать прямыми тонкими капиллярами, поэтому верно будет соотношение Хагена–Пуазейля: Q= ε S r 2 ΔP , 8ηW ΔL (3) где ε – пористость поверхности, ∆P – разница давлений через мембрану, ∆L – толщина мембраны, r – радиус поры, η – вязкость проникающей жидкости, W – фактор извилистости пор. Величина ε представляет собой пористость поверхности, которая характеризует удельную поверхность пор, и равна отношению поверхности поры к поверхности мембраны: ε= n pS r Am 2 , (4) где np – число пор, r – радиус поры, Am – площадь поверхности мембраны. а Рис. 2. Расчетная сетка для половолоконной мембраны и окружающей ее культуральной жидкости б В результате моделирования спроектирована расчетная сетка мембранного волокна и культуральной жидкости, прилегающей к внешней части волокна (рис. 2). Получено скоростное Рис. 3. Распределение скоростей потока питательной среды в половолоконной мембране и окружающей ее культуральной жидкости: а) проницаемость мембраны максимальна; б) снижение проницаемости мембраны Воробьёва Екатерина Сергеевна, студентка 5 курса факультета Информационных технологий и управления РХТУ им. Д.И. Менделеева, Россия, Москва. Сафаров Руслан Рафигович, соискатель кафедры Кибернетики химико-технологических процессов РХТУ им. Д.И. Менделеева, Россия, Москва. Гусева Елена Владимировна, к.т.н., доцент кафедры Кибернетики химико-технологических процессов РХТУ им. Д.И. Менделеева, Россия, Москва. Меньшутина Наталья Васильевна, д.т.н., профессор кафедры Кибернетики химико-технологических процессов РХТУ им. Д.И. Менделеева, Россия, Москва. 73 Успехи в химии и химической технологии. ТОМ XXIX. 2015. № 4 Литература 1. CFD simulations of membrane filtration zone in a submerged hollow fibre membrane bioreactor using a porous media approach / Wang Y. [et al.]. Journal of Membrane Science. – 2010. V. 3. № 63. – P. 57-66. 2. Safarov R., Guseva E., Menshutina N. Application of CFD to model batch and membrane bioreactors// Proceedings of 21st International Congress of Chemical and Process Engineering CHISA 2014 Prague 17th Conference on Process Integration, Modelling and Optimisation for Energy Saving and Pollution Reduction, 2014, Prague, Czech Republic. Vorobiova Ekaterina Sergeevna*, Safarov Ruslan Rafigovich, Guseva Elena Vladimirovna, Menshutina Natalia Vasilevna D. Mendeleev University of Chemical Technology of Russia, Moscow, Russia. * e-mail: emulsja@rambler.ru SIMULATION OF HYDRODINAMICS IN THE HOLLOW FIBER MEMBRANE FOR CULTIVATION OF MAMMALIAN CELLS Abstract Using the software ANSYS Fluent 14.5 the simulation of mammalian cells growth in the hollow fiber membrane bioreactor has been done. Hollow fiber membrane is made from polysulfone. As the simulation results the flowrates distribution in inside membrane space and near membrane surface in interfibrillar space have been received. Key words: ANSYS Fluent 14.5, CFD simulation, hollow fiber membrane, hydrodinamics. 74






