1. УГОЛ НАКЛОНА прямОЙ
реклама
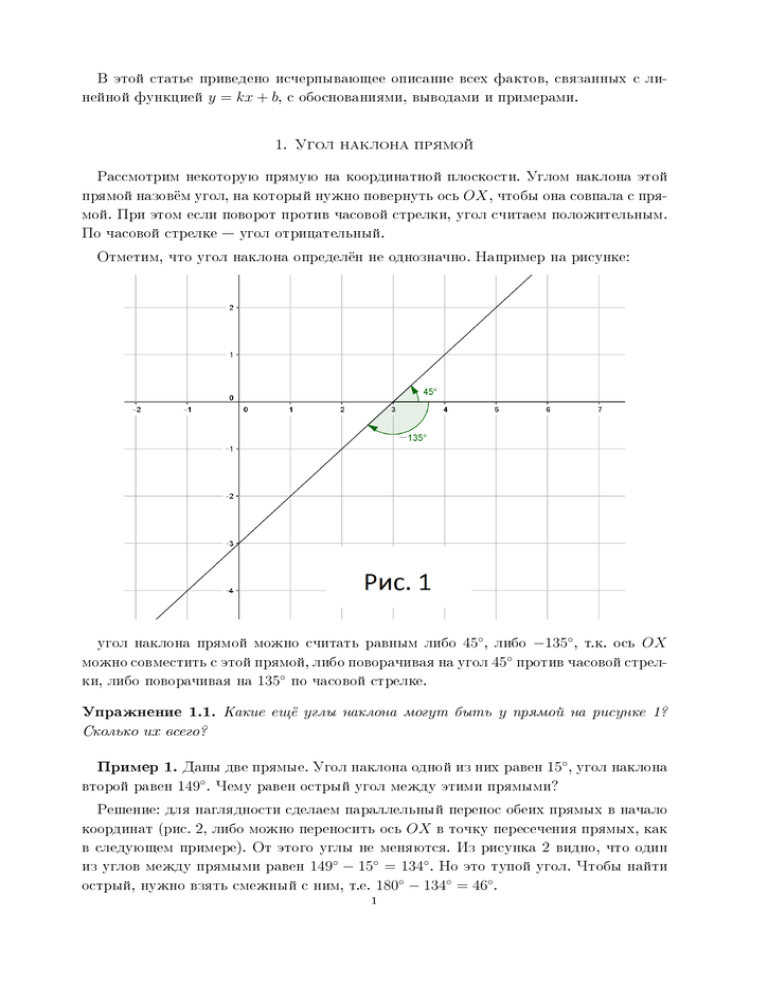
 ýòîé ñòàòüå ïðèâåäåíî èñ÷åðïûâàþùåå îïèñàíèå âñåõ ôàêòîâ, ñâÿçàííûõ ñ ëèíåéíîé ôóíêöèåé y = kx + b, ñ îáîñíîâàíèÿìè, âûâîäàìè è ïðèìåðàìè. 1. Óãîë íàêëîíà ïðÿìîé Ðàññìîòðèì íåêîòîðóþ ïðÿìóþ íà êîîðäèíàòíîé ïëîñêîñòè. Óãëîì íàêëîíà ýòîé ïðÿìîé íàçîâ¼ì óãîë, íà êîòîðûé íóæíî ïîâåðíóòü îñü OX , ÷òîáû îíà ñîâïàëà ñ ïðÿ- ìîé. Ïðè ýòîì åñëè ïîâîðîò ïðîòèâ ÷àñîâîé ñòðåëêè, óãîë ñ÷èòàåì ïîëîæèòåëüíûì. Ïî ÷àñîâîé ñòðåëêå óãîë îòðèöàòåëüíûé. Îòìåòèì, ÷òî óãîë íàêëîíà îïðåäåë¼í íå îäíîçíà÷íî. Íàïðèìåð íà ðèñóíêå: ◦ ëèáî −135 , ò.ê. îñü OX ◦ ìîæíî ñîâìåñòèòü ñ ýòîé ïðÿìîé, ëèáî ïîâîðà÷èâàÿ íà óãîë 45 ïðîòèâ ÷àñîâîé ñòðåë◦ êè, ëèáî ïîâîðà÷èâàÿ íà 135 ïî ÷àñîâîé ñòðåëêå. óãîë íàêëîíà ïðÿìîé ìîæíî ñ÷èòàòü ðàâíûì ëèáî Óïðàæíåíèå 1.1. 45◦ , Êàêèå åù¼ óãëû íàêëîíà ìîãóò áûòü ó ïðÿìîé íà ðèñóíêå 1? Ñêîëüêî èõ âñåãî? Ïðèìåð 1. ◦ Äàíû äâå ïðÿìûå. Óãîë íàêëîíà îäíîé èç íèõ ðàâåí 15 , óãîë íàêëîíà ◦ âòîðîé ðàâåí 149 . ×åìó ðàâåí îñòðûé óãîë ìåæäó ýòèìè ïðÿìûìè? Ðåøåíèå: äëÿ íàãëÿäíîñòè ñäåëàåì ïàðàëëåëüíûé ïåðåíîñ îáåèõ ïðÿìûõ â íà÷àëî êîîðäèíàò (ðèñ. 2, ëèáî ìîæíî ïåðåíîñèòü îñü OX â òî÷êó ïåðåñå÷åíèÿ ïðÿìûõ, êàê â ñëåäóþùåì ïðèìåðå). Îò ýòîãî óãëû íå ìåíÿþòñÿ. Èç ðèñóíêà 2 âèäíî, ÷òî îäèí ◦ ◦ ◦ èç óãëîâ ìåæäó ïðÿìûìè ðàâåí 149 − 15 = 134 . Íî ýòî òóïîé óãîë. ×òîáû íàéòè ◦ ◦ ◦ îñòðûé, íóæíî âçÿòü ñìåæíûé ñ íèì, ò.å. 180 − 134 = 46 . 1 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí +79265460671 www.UnderMath.ru Ýòó çàäà÷ó ìîæíî ðåøèòü è áåç ðèñóíêà, òîëüêî àáñòðàêòíûìè ðàññóæäåíèÿìè. Íà÷◦ í¼ì ïîâîðà÷èâàòü îñü OX . Âíà÷àëå ìû å¼ ïîâîðà÷èâàåì íà 15 , è îíà îêàæåòñÿ ïàðàëëåëüíà ïåðâîé ïðÿìîé. Çàòåì ìû å¼ äîâîðà÷èâàåì åù¼ íà êàêîé-òî óãîë α, òàê ÷òî ◦ â èòîãå îíà îêàçûâàåòñÿ ïîâ¼ðíóòîé íà 149 è ïàðàëëåëüíà âòîðîé ïðÿìîé. Çíà÷èò 15◦ + α = 149◦ , ò.å. α = 134◦ . Ýòîò óãîë α ýòî óãîë, íà êîòîðûé íóæíî äîâåðíóòü ïåðâóþ ïðÿìóþ, ÷òîáû îíà îêàçàëàñü ïàðàëëåëüíà âòîðîé. Ò.å. ýòî îäèí èç óãëîâ ìåæäó ïðÿìûìè. Äàëüøå òî æå, ÷òî â ïðåäûäóùåì ðàññóæäåíèè: óãîë òóïîé, ïîýòîìó áåð¼ì ñìåæíûé ñ íèì îñòðûé. Ïðèìåð 2. ◦ Äàíû äâå ïðÿìûå. Óãîë íàêëîíà îäíîé èç íèõ ðàâåí 39 , óãîë íàêëîíà ◦ âòîðîé ðàâåí −18 . ×åìó ðàâåí îñòðûé óãîë ìåæäó ýòèìè ïðÿìûìè? Ðàññóæäåíèå òàêîå æå, ÷òî â ïðåäûäóùåì ïðèìåðå. Åñëè ðåøàòü ïî ðèñóíêó: îòâåò 39◦ + 18◦ = 57◦ . Åñëè ðåøàòü ñ ïîìîùüþ ïîâîðîòîâ, òî Ïîñêîëüêó óãîë Ïðèìåð 3. 57◦ −18◦ + α = 39◦ ⇒ α = 57◦ . îñòðûé, áðàòü ñìåæíûé ñ íèì óãîë íå òðåáóåòñÿ. ◦ Äàíû äâå ïðÿìûå. Óãîë íàêëîíà îäíîé èç íèõ ðàâåí 156 , óãîë íàêëîíà ◦ âòîðîé ðàâåí −148 . ×åìó ðàâåí îñòðûé óãîë ìåæäó ýòèìè ïðÿìûìè? Ðåøåíèå ñ ïîìîùüþ ðèñóíêà ïðîâåäèòå ñàìîñòîÿòåëüíî. ◦ Ðåøåíèå ñ ïîìîùüþ ïîâîðîòîâ: −148 + α = 180◦ , ïîýòîìó ðåàëüíûé óãîë ìåæäó ïðÿìûìè 2 156◦ ⇒ α = 304◦ . Íî ýòîò óãîë áîëüøå 360◦ − 304◦ = 56◦ . Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí Óïðàæíåíèå 1.2. +79265460671 www.UnderMath.ru Çàïîëíèòå òàáëèöó: Óãîë íàêëîíà ïåðâîé ïðÿìîé ◦ −144 260◦ 175◦ 91◦ 139◦ Óïðàæíåíèå 1.3. Óãîë íàêëîíà âòîðîé ïðÿìîé ◦ Îñòðûé óãîë ìåæäó ïðÿìûìè 11 −80◦ −150◦ 125◦ 16◦ Íàïèøèòå îáùåå ïðàâèëî âû÷èñëåíèÿ óãëà ìåæäó ïðÿìûìè, îäíà èç êîòîðûõ íàêëîíåíà ïîä óãëîì Óïðàæíåíèå 1.4. α, âòîðàÿ ïîä óãëîì β. (1) Ìîæåò ëè áûòü ó îäíîé è òîé æå ïðÿìîé äâà ðàçíûõ óãëà íàêëîíà? (2) Ìîæåò ëè áûòü ó äâóõ ðàçëè÷íûõ ïðÿìûõ îäèí è òîò æå óãîë íàêëîíà? (3) Ìîæåò ëè áûòü ó äâóõ íåïàðàëëåëüíûõ ïðÿìûõ îäèí è òîò æå óãîë íàêëî- íà? 2. Òàíãåíñ óãëà íàêëîíà, óãëîâîé êîýôôèöèåíò Èç ïðåäûäóùåãî ïóíêòà ìû óâèäåëè, ÷òî ó îäíîé è òîé æå ïðÿìîé ìîæåò áûòü ◦ ìíîãî óãëîâ íàêëîíà âèäà α + 180 · n, ãäå n = 0, ±1, ±2 . . . ×òîáû èçáåæàòü ïóòàíèöû (à òàêæå è ïî äðóãèì ïðè÷èíàì, ñì. äàëåå), ïðèíÿòî èñïîëüçîâàòü íå ñàì óãîë íàêëîíà, à åãî òàíãåíñ. Åñëè ïðÿìàÿ íàêëîíåíà ïîä óãëîì α, òî âåëè÷èíà tg α íàçûâàåòñÿ óãëîâûì êîýôôèöèåíòîì ïðÿìîé. Ïðè òàêîì îïðåäåëåíèè ïðîáëåìà ìíîãîçíà÷íîñòè èñ÷åçàåò, ò.å. ó êàæäîé ïðÿìîé ðîâíî îäèí óãëîâîé êîýôôèöèåíò. Äåéñòâèòåëüíî, âîçüì¼ì ïðÿìóþ íà ðèñ.1. Ïî◦ ◦ ◦ ◦ ñêîëüêó tg 45 = tg(−135 ) = 1, è âîîáùå tg(45 + 180 · n) = 1 ïðè ëþáîì öåëîì n, óãëîâîé êîýôôèöèåíò ýòîé ïðÿìîé ðàâåí 1 íåçàâèñèìî îò òîãî, êàêîé èç óãëîâ ñ÷èòàòü óãëîì íàêëîíà. Óïðàæíåíèå 2.1. Ìîæåò ëè áûòü ó äâóõ íåïàðàëëåëüíûõ ïðÿìûõ îäèí è òîò æå óãëîâîé êîýôôèöèåíò? Óïðàæíåíèå 2.2. ×åìó ðàâåí óãëîâîé êîýôôèöèåíò áèññåêòðèñû ïåðâîãî êîîðäè- íàòíîãî óãëà (ò.å. áèññåêòðèñû óãëà ìåæäó îñÿìè êîîðäèíàò, ïðîõîäÿùåé â ïåðâîé è òðåòåé ÷åòâåðòÿõ)? Òîò æå âîïðîñ äëÿ áèññåêòðèñû âòîðîãî êîîðäèíàòíîãî óãëà. Óïðàæíåíèå√2.3. ðàâåí à) 0, á) ×åìó ðàâåí óãîë íàêëîíà ïðÿìîé, óãëîâîé êîýôôèöèåíò êîòîðîé √ 3, â) - 3, ã) √13 , ä) − √13 , å) 2, æ) 12 ? Óïðàæíåíèå 2.4. ×åìó ðàâåí óãëîâîé êîýôôèöèåíò ïðÿìîé, ïàðàëëåëüíîé îñè îð- äèíàò? Óïðàæíåíèå 2.5. (1) ×åìó ðàâåí îñòðûé óãîë ìåæäó äâóìÿ ïðÿìûìè, óãëîâûå êîýôôèöèåíòû êîòîðûõ ðàâíû 3 è 2? (2) ×åìó ðàâåí îñòðûé óãîë ìåæäó äâóìÿ ïðÿìûìè, óãëîâûå êîýôôèöèåíòû êî- òîðûõ ðàâíû -3 è -2? 3 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí +79265460671 www.UnderMath.ru (3) ×åìó ðàâåí îñòðûé óãîë ìåæäó ïðÿìûìè, óãëîâûå êîýôôèöèåíòû êîòîðûõ ðàâíû 3 è -2? (Íåçàâèñèìî îò òîãî, ðåøèëè âû ýòî óïðàæíåíèå èëè íåò, ðåêîìåíäóþ î÷åíü âíèìàòåëüíî ïðî÷èòàòü ðåøåíèå) Óïðàæíåíèå 2.6. Çàïîëíèòå òàáëèöó (ïåðâàÿ ñòðîêà îáðàçåö): Óãë. êîýôô. ïåðâîé ïðÿìîé Óãë. êîýôô. âòîðîé ïðÿìîé 2 1 -0.5 3 0.6 1.5 1 -2 1 -1 Óïðàæíåíèå 2.7. Âûâåäèòå îáùóþ ôîðìóëó îñòðîãî óãëà ìåæäó ïðÿìûìè, óãëî- âûå êîýôôèöèåíòû êîòîðûõ ðàâíû Óïðàæíåíèå 2.8. Îñòðûé óãîë ìåæäó ïðÿìûìè arctg 13 k1 è k2 . Êàêîé îñîáûé ñëó÷àé íå ðàçîáðàí â ðåøåíèè ïðåäûäóùåãî óïðàæ- íåíèÿ? ×åìó ðàâåí óãîë ìåæäó ïðÿìûìè â ýòîì ñëó÷àå? 3. Ïðÿìàÿ è òî÷êè íà íåé Ïóñòü íà êîîðäèíàòíîé ïëîñêîñòè äàíû äâå òî÷êè â òî÷êó B, è B(4, 5) (ðèñ 4). Ïóñòü AB , à âíà÷àëå ïî ãîðèçîíòàëè (âäîëü îñè OX ), çàòåì ïî âåðòèêàëè (âäîëü îñè OY ). Ïî ãîðèçîíòàëè åìó íóæíî áóäåò ïðîéòè ðàññòîÿíèå 4 − 1 = 3, à ïî âåðòèêàëè 5 − 3 = 2. Áóäåì íàçûâàòü ýòè ðàññòîÿíèÿ ñìåùåíèÿìè ïî x è ïî y è îáîçíà÷àòü 4x è 4y . Òàêèì îáðàçîì, â äàííîì ñëó÷àå 4x = 3, 4y = 2. íåêòî ïåðåìåùàåòñÿ èç òî÷êè A A(1, 3) ïðè÷¼ì äåëàåò ýòî íå ïî ïðÿìîé Åñëè ïåðåìåùåíèå ïðîèñõîäèò îò áîëüøåé êîîðäèíàòû ê ìåíüøåé, òî çíàê ïåðåìåùåíèÿ áóäåò îòðèöàòåëüíûì. Íàïðèìåð íà ðèñ 5 4x = −3, 4y = −2, íà ïðîèñõîäèò èç A â B ). ðèñ 7 4x = −2, 4y = +7 4 4x = 2, 4y = −7, íà ðèñ 6 (íà âñåõ ðèñóíêàõ ïåðåìåùåíèå Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí Óïðàæíåíèå 3.1. +79265460671 Çàïèøèòå âûðàæåíèÿ äëÿ ùåíèå ïðîèñõîäèò îò òî÷êè A(x1 , y1 ) ê òî÷êå 4x, 4y â B(x2 , y2 ). www.UnderMath.ru îáùåì âèäå, åñëè ïåðåìå- Âåðí¼ìñÿ ê ðèñ. 4. Çàìåòèì, ÷òî â ïîëó÷èâøåìñÿ òàêèì îáðàçîì ïðÿìîóãîëüíîì òðåóãîëüíèêå ABC ∠BAC â òî÷íîñòè ðàâåí óãëó íàêëîíà ïðÿìîé 4y BC óãëà ðàâåí = 4x . AC AB , à òàíãåíñ ýòîãî Òåïåðü îáðàòèìñÿ ê ðèñ. 5. Ïîíÿòíî, ÷òî ñèòóàöèÿ ïî÷òè àíàëîãè÷íà, íî íóæíî ïðîñëåäèòü çà çíàêàìè. Ïðÿìàÿ íàêëîíåíà âíèç, óãîë íàêëîíà îòðèöàòåëüíûé ◦ (åñëè áûòü òî÷íûì, íóæíî ñêàçàòü, ÷òî îí èç èíòåðâàëà (−90 , 0)), ïîýòîìó óãëîâîé êîýôôèöèåíò äîëæåí áûòü îòðèöàòåëüíûì. Ýòî ñîãëàñóåòñÿ ñ ôîðìóëîé: 4y = − 72 . 2, 4y = −7, 4x 4x = Èòàê, ìû ïîëó÷èëè, ÷òî â îáîèõ ñëó÷àÿõ (1) Óãëîâîé êîýôôèöèåíò ïðÿìîé Óïðàæíåíèå 3.2. AB = 4y 4x Óáåäèòåñü, ÷òî â îñòàâøèõñÿ äâóõ ñëó÷àÿõ (ðèñ.6 è ðèñ.7) ýòà ôîðìóëà òîæå âåðíà. Ãëàâíîå, ÷òî íóæíî ïðîâåðèòü ñîâïàäåíèå çíàêîâ.  ìàòåìàòèêå ðàçáîð ïðèìåðà ñ êîíêðåòíûìè ÷èñëàìè íå ñ÷èòàåòñÿ äîêàçàòåëüñòâîì, ïîýòîìó Óïðàæíåíèå 3.3. Ïîâòîðèòå ðàññóæäåíèå â îáùåì âèäå: äîêàæèòå ôîðìóëó (1) äëÿ òî÷åê ñ ïðîèçâîëüíûìè êîîðäèíàòàìè Óïðàæíåíèå 3.4. Çàïîëíèòå òàáëèöó: Êîîðäèíàòû òî÷êè 1.5. A Êîîðäèíàòû òî÷êè (1,2) (3,-5) (0,0) (5,3) (-7,1) (4,1) (1,3) (1,4) (-1,2) (3,5) Ïðèìåð 4. A(x1 , y1 ), B(x2 , y2 ). Óãëîâîé êîýôôèöèåíò ïðÿìîé AB A(3, −7) ïðîâåäåíà ïðÿìàÿ l ñ óãëîâûì êîýôôèöèåíòîì òî÷åê B(6, 1), C(7, −1), D(13, 8) ëåæàò íà ýòîé ïðÿìîé. ×åðåç òî÷êó Îïðåäåëèòå, êàêèå èç B 5 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí +79265460671 www.UnderMath.ru Ðåøåíèå. Âû÷èñëÿåì óãëîâîé êîýôôèöèåíò ïðÿìîé AB . 4x = 6 − 3 = 3, 4y = 4y = 83 6= 1.5, ò.å. ïðÿìàÿ AB íå ñîâïàäàåò ñ ïðÿìîé l, à çíà÷èò òî÷êà − (−7) = 8, 4x 1 B íå ëåæèò íà l . C Äëÿ òî÷åê è D âû÷èñëÿåì, ÷òî óãëîâûå êîýôôèöèåíòû ïðÿìûõ 1.5. Ýòî çíà÷èò, ÷òî òî÷êè ÷åðåç òî÷êó A C è D ëåæàò íà ïðÿìîé l, AC è AD ðàâíû ò.ê. èíà÷å ïîëó÷èëîñü áû, ÷òî ïðîõîäÿò ðàçëè÷íûå ïðÿìûå ñ îäèíàêîâûì óãëîâûì êîýôôèöèåíòîì, ÷òî íåâîçìîæíî. Óïðàæíåíèå 3.5. ôèöèåíòàìè 3 è ×åðåç òî÷êó −2. A(1, 2) ïðîâåäåíû ïðÿìûå l1 è l2 ñ óãëîâûìè êîýô- Äëÿ êàæäîé èç òî÷åê B(3, 7), C(4, 11), D(0, 4), E(111, −218), F (221, 663) îïðåäåëèòå, ëåæèò ëè îíà íà êàêîé-íèáóäü èç ïðÿìûõ l1 , Óïðàæíåíèå 3.6. Âåðíî ëè, ÷òî òðè òî÷êè l2 ? A(−17, −41), B(3, −11), C(25, 22) ëå- æàò íà îäíîé ïðÿìîé? Çàäà÷ó íóæíî ðåøèòü, íå äåëàÿ ðèñóíêîâ. Óïðàæíåíèå 3.7. Âûâåäèòå â îáùåì âèäå óñëîâèå ðàñïîëîæåíèÿ òî÷åê A(x1 , y1 ), B(x2 , y2 ), C(x3 , y3 ) íà îäíîé ïðÿìîé. Çàïîëíèòå òàáëèöó: A, B, C (1, 2); (5, 6); (139, 140) (7, 2); (13, −10); (100, −140) (−3, 19); (0, 14); (30, −36) (8, 2); (8, 11); (8, 129) (−100, 100); (−20, 96); (0, 95) Êîîðäèíàòû òî÷åê Ïðèìåð 5. Ëåæàò íà îäíîé ïðÿìîé (äà/íåò) A(3, 4)) ïðîâåäåíà ïðÿìàÿ ñ óãëîâûì êîýôôèöèåíòîì 1.5. Íà íåé âûáðàíà òî÷êà B . Çíàÿ, ÷òî àáñöèññà òî÷êè B ðàâíà 17, íàéäèòå å¼ îðäèíàòó. ×åðåç òî÷êó Ðåøåíèå. Ïåðâûé ñïîñîá: óãëîâîé êîýôôèöèåíò 1.5 îçíà÷àåò, ÷òî ïåðåìåùàÿñü íà a åäèíèö âäîëü OX , ìû ïåðåìåùàåìñÿ íà 1.5a åäèíèö âäîëü OY . ×òîáû ïîïàñòü èç A â B , íóæíî ïåðåìåñòèòüñÿ íà 17 − 3 = 14 åäèíèö âïðàâî, è çíà÷èò íà 1.5 · 14 = 21 åäèíèö ââåðõ, ò.å. îðäèíàòà òî÷êè B ðàâíà 4 + 21 = 25. Çàïèøåì ïåðåìåùåíèÿ èç A â 4y B : 4x = 17 − 3 = 14, 4y = y − 4. Âû÷èñëÿåì 4x è ïðèðàâíèâàåì ê óãëîâîìó êîýôôèöèåíòó. Ïîëó÷àåì óðàâíåíèå: Âòîðîé ñïîñîá: ïóñòü îðäèíàòà òî÷êè Óïðàæíåíèå 3.8. B ðàâíà y. y−4 = 1.5 ⇒ y = 25. 14 ×åðåç òî÷êó Íà ïðÿìîé âçÿòà òî÷êà B, A ïðîâåäåíà ïðÿìàÿ ñ óãëîâûì êîýôôèöèåíòîì k. ó êîòîðîé èçâåñòíà òîëüêî îäíà êîîðäèíàòà. Íàéäèòå 6 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí âòîðóþ êîîðäèíàòó òî÷êè B +79265460671 www.UnderMath.ru ïî äàííûì òàáëèöû: A è êîýôôèöèåíò k A(2, 3), k = −1 A(1, −2), k = 34 A(−2, 6), k = −3 A(−1, 4), k = 1 A(11, 3), k = −2 A(0, 2), k = 12 Êîîðäèíàòû êîîðäèíàòû B íåäîñòàþùàÿÿ êîîðäèíàòà B B(19, ...) B(11, ...) B(−10, ...) B(..., 11) B(..., 1) B(..., 30) 4. Óðàâíåíèå ïðÿìîé Èç øêîëüíîãî êóðñà õîðîøî èçâåñòíî, ÷òî ãðàôèêîì ôóíêöèè y = kx + b ÿâëÿåòñÿ ïðÿìàÿ. Òåîðåìà. Óãëîâîé êîýôôèöèåíò ïðÿìîé, çàäàâàåìîé óðàâíåíèåì y = kx + b, ðàâåí k. Äîêàçàòåëüñòâî. Âûáåðåì íà ïðÿìîé äâå ïðîèçâîëüíûå òî÷êè öèññû ðàâíû x1 è x2 A è B, ïóñòü èõ àáñ- (ðèñ. 8). Îðäèíàòû ýòèõ òî÷åê âûðàçèì ÷åðåç óðàâíåíèå ïðÿìîé: y1 = kx1 + b, y2 = kx2 + b. Âû÷èñëÿåì óãëîâîé êîýôôèöèåíò: 4x = x2 − x1 , 4y = y2 − y1 = kx2 + b − (kx1 + b) = k(x2 − x1 ), 4y = k. 4x ×òî è òðåáîâàëîñü. 7 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí Ïðèìåð 6. +79265460671 www.UnderMath.ru Ñîñòàâèòü óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êó A(2; 3) ñ óãëî- 5. Ðåøåíèå. Ïóñòü B(x; y) ïðîèçâîëüíàÿ òî÷êà íà ïðÿìîé. Çàïèøåì óãëîâîé êîýôôèöèåíò ÷åðåç òî÷êè A, B : y−3 =5 k= x−2 îòêóäà y = 5x − 7 èñêîìîå óðàâíåíèå. âûì êîýôôèöèåíòîì Ïðèìåð 7. Çàïèñàòü îáùåå óðàâíåíèå ïðîèçâîëüíîé ïðÿìîé, ïðîõîäÿùåé ÷åðåç A(2; 3). òî÷êó Ðåøåíèå.  ïðåäûäóùåì ïðèìåðå íóæíî ïîäñòàâèòü k= Ïðè èçìåíåíèè êè k k âìåñòî 5: y−3 ⇒ y = k(x − 2) + 3. x−2 ïðÿìàÿ, çàäàâàåìàÿ ýòèì óðàâíåíèåì, áóäåò âðàùàòüñÿ âîêðóã òî÷- A(2; 3). Óïðàæíåíèå 4.1. A òî÷êà Çàïîëíèòå òàáëèöó (ïåðâàÿ ñòðîêà îáðàçåö): óãë.êîýôô (2;3) 5 (1;5) -2 (3;3) 0 (-3;-8) k t (0;0) k Añ 5x − y − 7 = 0 óð. ïðÿìîé, ïðîõ. ÷åðåç óãë. êîýô k Ýòî æå óðàâíåíèå ìîæíî ïîëó÷èòü èç äðóãèõ ðàññóæäåíèé: ïðÿìàÿ ëþáîì k ïðîõîäèò ÷åðåç íà÷àëî êîîðäèíàò O. íå¼ ñäâèãîì íà 2 âïðàâî è íà 3 ââåðõ, ò.å. ïðîõîäèò Ïðèìåð 8. èçìåíåíèè y = k(x − 2) + 3 ÷åðåç (2; 3). Ïðÿìàÿ y = kx ïîëó÷åíà èç y = ax − 2a − 4 Íàéòè òî÷êó, âîêðóã êîòîðîé âðàùàåòñÿ ïðÿìàÿ ïðè ïðè a. y+4 y + 4 = a(x − 2) ⇒ a = x−2 . Îòñþäà âèäíî, ÷òî ýòî óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êó (2; −4) ñ óãëîâûì êîýôôèöèåíòîì a. Ðåøåíèå. Çàïèøåì óðàâíåíèå â âèäå Ïðèìåð 9. èçìåíåíèè Íàéòè òî÷êó, âîêðóã êîòîðîé âðàùàåòñÿ ïðÿìàÿ y = 3ax + 2x − 4 ïðè a. y + 4 = x(3a + 2) ⇒ 3a + 2 = y+4 . Îòñþäà âèäíî, x ÷òî ýòî óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êó (0; −4) ñ óãëîâûì êîýôôèöèåíòîì 3a + 2. Ðåøåíèå. Çàïèøåì óðàâíåíèå â âèäå Ïðèìåð 10. ïðè èçìåíåíèè Íàéòè òî÷êó, âîêðóã êîòîðîé âðàùàåòñÿ ïðÿìàÿ y = 3ax + 2x − 4 − a a. Ðåøåíèå. Çäåñü ñëîæíåå. Äëÿ íà÷àëà çàïèøåì êàê â ïðåäûäóùåì ïðèìåðå: y + 4 = x(3a + 2) − a. Âû÷òåì 2 èç îáåèõ ÷àñòåé: 3 2 1 1 y + 4 = x(3a + 2) − a + = x(3a + 2) − (3a + 2) = x − (3a + 2). 3 3 3 8 Ãåîðãèé Ñåìåíîâè÷ Ìóòàôÿí +79265460671 Îòñþäà âèäíî, ÷òî ýòî ïðÿìàÿ, ïðîõîäÿùàÿ ÷åðåç Óïðàæíåíèå 4.2. www.UnderMath.ru 1 ; −4 . 3 Íàéòè òî÷êó, âîêðóã êîòîðîé âðàùàåòñÿ êàæäàÿ èç ïåðå÷èñ- ëåííûõ íèæå ïðÿìûõ ïðè èçìåíåíèè a: y = a(x − 2) + 1; y = (a + 1)(x − 2) + 1; y = 5ax + 4 − 3a − x; ay = 2x + 4a − 3 + y; 3y = 2ax − x − 3a; (a − 1)x − 2y + 3a − 2 = 0. Ïðèìåð 11. Ñîñòàâèòü óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êè Ðåøåíèå. Ðàññóæäåíèå àíàëîãè÷íî óïð. 3.7. Ïóñòü ïðÿìîé. Çàïèñûâàåì óñëîâèå ðàñïîëîæåíèÿ òî÷åê A(2; 3) è B(6; 4). C(x; y) ïðîèçâîëüíàÿ òî÷êà A, B, C íà îäíîé ïðÿìîé: íà y−3 4−3 = x−2 6−2 îòêóäà 4y = x + 10 Óïðàæíåíèå 4.3. òî÷êà A òî÷êà èñêîìîå óðàâíåíèå. B (2;3) (6;4) (1;5) (0;-7) (3;3) (6;3) (-3;-8) (-4;-9) (3;4) (3;7) Óïðàæíåíèå 4.4. Çàïîëíèòå òàáëèöó (ïåðâàÿ ñòðîêà îáðàçåö): AB x − 4y + 10 = 0 óð. ïðÿìîé Ñîñòàâüòå óðàâíåíèå ïðÿìîé, ïðîõîäÿùåé ÷åðåç òî÷êó ïåðïåíäèêóëÿðíî ïðÿìîé 3x − 2y + 5 = 0. Óêàçàíèå: âñïîìíèòå óïð. 2.8. 9 A(2; 3)