Предмет: геометрия

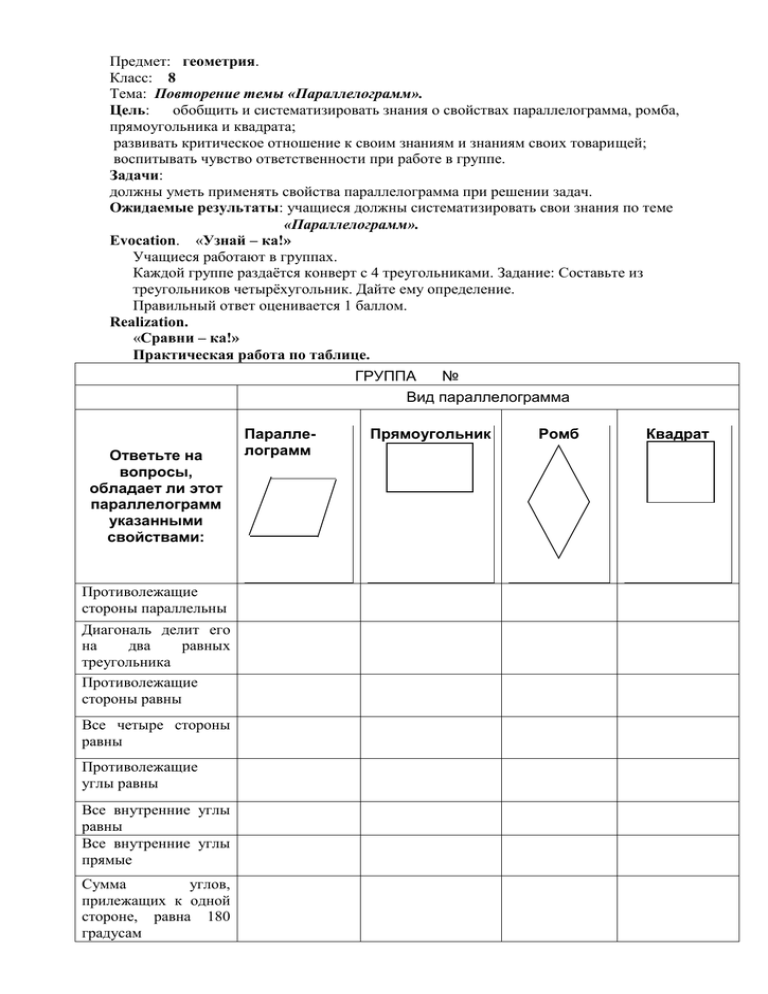
Предмет: геометрия.
Класс: 8
Тема: Повторение темы «Параллелограмм».
Цель:
обобщить и систематизировать знания о свойствах параллелограмма, ромба,
прямоугольника и квадрата;
развивать критическое отношение к своим знаниям и знаниям своих товарищей;
воспитывать чувство ответственности при работе в группе.
Задачи:
должны уметь применять свойства параллелограмма при решении задач.
Ожидаемые результаты: учащиеся должны систематизировать свои знания по теме
«Параллелограмм».
Evocation. «Узнай – ка!»
Учащиеся работают в группах.
Каждой группе раздаётся конверт с 4 треугольниками. Задание: Составьте из
треугольников четырёхугольник. Дайте ему определение.
Правильный ответ оценивается 1 баллом.
Realization.
«Сравни – ка!»
Практическая работа по таблице.
ГРУППА
№
Вид параллелограмма
Ответьте на
вопросы,
обладает ли этот
параллелограмм
указанными
свойствами:
Противолежащие
стороны параллельны
Диагональ делит его
на
два
равных
треугольника
Противолежащие
стороны равны
Все четыре стороны
равны
Противолежащие
углы равны
Все внутренние углы
равны
Все внутренние углы
прямые
Сумма
углов,
прилежащих к одной
стороне, равна 180
градусам
Параллелограмм
Прямоугольник
Ромб
Квадрат
Диагонали
пересекаются
и
точкой пересечения
делятся пополам
Диагонали равны
Диагонали
пересекаются
под
прямым углом
Диагонали
делят
противолежащие
углы пополам
Если четырехугольник облает указанным свойством, то в соответствующей клеточке
ставим +, если нет, то -.
Даётся время для обсуждения в группах.
Потом группы меняются работами для взаимопроверки.
Вопросы для взаимопроверки:
1. Какими свойствами обладают и параллелограмм, и прямоугольник, и ромб, и
квадрат? Почему?
2. Какими свойствами обладают и прямоугольник, и квадрат? Почему?
3. Какими свойствами обладают и ромб, и квадрат? Почему?
Правильные ответы оценивается 1 баллом.
Reflection.
«Решай – ка!»
Калейдоскоп задач «Ромашка»: по одной задаче на группу. Возможные ответы на
сердцевине цветка.
1. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр и
углы треугольника AOB , если CAD =30; АС =12cм.
2. На стороне BC параллелограмма ABCD взята точка M , так что
AB =BM .
а) найдите периметр параллелограмма, если CD =8 см ; CM =4 см.
б) докажите, что AM –биссектриса BAD .
3. Периметр ромба равен 56 см , высота, проведённая из вершины тупого угла , делит
сторону ромба пополам.
Определите углы ромба, длину диагонали, проведённой из этой же вершины.
4. Найдите углы ромба , если диагонали составляют с его стороной углы , один из
которых на 20  меньше другого.
5. Меньшая сторона АВ прямоугольника ABCD равна 5 см. и образует с диагональю угол
60. Найдите диагонали прямоугольника и периметр треугольника COD ( О – точка
пересечения его диагоналей), и его углы.
6. Углы, образованные диагоналями ромба с одной из его сторон, относятся как 1:4.
Найдите углы ромба.
7. Биссектриса угла А параллелограммаABCD образует со стороной АВ угол в 35 и
делит сторону ВС на части, равные 2 см. и 6 см. Найдите периметр параллелограмма
и его углы.
8. Диагональ ромба образует с одной из его сторон угол в 60  и равна 10 см. Найдите
периметр ромба и его углы.
Каждая группа должна письменно разобрать задачу. Правильное решение оценивается
1 баллом. За правильный ответ на дополнительный вопрос группа оценивается ещё
одним баллом. Дополнительный вопрос к задаче: Какие свойства параллелограмма
были использованы при решении?
Итог урока: Группа, набравшая большее количество баллов, награждается званием
«Знаток параллелограмма».