Аналитическая справка Анализ результатов выполнения городской диагностической контрольной работы

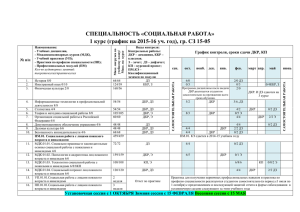
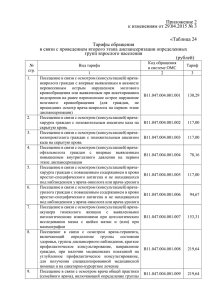
Аналитическая справка
Анализ результатов
выполнения городской диагностической контрольной работы
по математике в 9 классе (10.04.2012)
I.
Формат и особенности ДКР
1.
2.
3.
На выполнение работы отводилось 4 часа (240 минут).
В содержание работы 2012 года были включены 6 задач по геометрии.
Для записи решений и ответов учащимся выдавались 1 бланк ответов АВ и 1-2 бланка ответов С.
4.
5.
Работа состояла из двух частей.
В первой части 18 заданий: А1 – А4, В1 – В11 и С1 – С3. Во второй части 5 заданий: С4 – С8.
При выполнении заданий первой части нужно было указывать только ответы. При этом:
 при выполнении заданий А1 – А4 ответы необходимо было занести в бланк ответов АВ под номером
выполняемого задания.
К каждому заданию А1 – А4 были приведены 4 варианта ответа, из которых только один верный.
 ответом на задания В1 – В10 было целое число или конечная десятичная дробь. Ответ следовало записать в бланк
ответов АВ справа от номера выполняемого задания, начиная с первой клеточки.
 ответом к заданию В11 являлась возрастающая последовательность номеров верных утверждений, записанных без
пробелов и использования других символов, например, 235.
 при исправлении неверного ответа в заданиях В1 – В11 необходимо было зачеркнуть старый ответ и справа без
пробела записать новый.
 при выполнении заданий С1 – С3 ответы необходимо было занести в бланк ответов С без решения. В случае
записи неверного ответа в заданиях следовало зачеркнуть его и написать новый.
Пользоваться калькуляторами и справочными таблицами не разрешалось.
1
II. Анализ результатов выполнения заданий ДКР по I части
При выполнении заданий I части учащиеся должны были продемонстрировать определенную системность знаний и широту
представлений. В ней проверялось не только владение базовыми алгоритмами, но и знание и понимание важнейших элементов содержания
(понятий, их свойств, приемов решения задач и пр.), умение пользоваться различными математическими языками, умение применять знания к
решению математических задач, не сводящихся к прямому применению алгоритмов, а также применение знаний в простейших практических
ситуациях.
2.1.
Результаты выполнения заданий
Процент правильных ответов
№ п/п
Обозначен
ие задания
в работе
Требования (умения), проверяемые заданиями
экзаменационной работы
Лицеи
Гимназии
Ууглубленное
изучение
предметов
СОШ
Др.учебн.
заведения
Итого
Выполнять разложение многочленов на множители
1
А1
79%
73%
75%
66%
65%
72%
92%
89%
87%
83%
82%
87%
80%
76%
73%
69%
63%
72%
63%
57%
56%
52%
52%
56%
80%
69%
67%
64%
70%
70%
93%
76%
90%
72%
89%
73%
86%
65%
86%
55%
89%
68%
Определять принадлежность точки графику функции
2
А2
Применять свойства арифметических квадратных корней для
преобразования
числовых
выражений,
содержащих
квадратные корни
3
А3
Применения теоремы
квадратного трехчлена
4
Виета
для
нахождения
корней
А4
Выполнять арифметические действия с рациональными
числами, находить в несложных случаях значения степеней с
целыми показателями; вычислять значения числовых
выражений; переходить от одной формы записи чисел к
другой
5
В1
Решать линейные уравнения
6
В2
В3
Определять значение функции по значению аргумента при
2
различных способах задания функции; интерпретировать
графики реальных зависимостей
7
Решать несложные практические
связанные с отношением, процентами
8
расчетные
задачи,
В4
76%
72%
70%
64%
58%
68%
84%
80%
76%
67%
68%
75%
71%
66%
60%
56%
61%
63%
85%
80%
77%
69%
56%
73%
63%
59%
57%
50%
62%
58%
76%
67%
66%
50%
62%
64%
71%
68%
64%
53%
49%
61%
10%
7%
12%
7%
9%
9%
66%
59%
57%
44%
39%
53%
72%
67%
62%
51%
52%
61%
67%
60%
53%
46%
54%
56%
Интерпретировать графики реальных зависимостей
9
В5
Сравнивать действительные числа; изображать числа точками
на координатной прямой
10
В6
Решать
планиметрические
задачи
геометрических величин (углов)
11
на
нахождение
В7
Сравнивать шансы наступления случайных
оценивать вероятности случайного события
12
событий,
В8
Решать практические задачи, связанные с нахождением
геометрических величин
13
В9
Решать текстовые задачи алгебраическим методом,
интерпретировать полученный результат, проводить отбор
решений исходя из формулировки задачи
14
В10
Оценивать
логическую
правильность
распознавать ошибочные заключения
15
рассуждений,
В11
Определять функцию по ее графику
16
С1
17
С2
18
С3
Составлять несложные формулы, выражающие зависимости
между величинами
Применять графические представления при решении
уравнений, систем, неравенств
3
2.2. Анализ неуспешных заданий
При выполнении заданий первой части работы (см. таблицу и диаграмму), как и предыдущие годы, наибольшие затруднения у учащихся
вызывают задания, решение которых требует применить умение пользоваться различными математическими языками, умение перейти от
одного языка к другому, умение применять знания к решению математических задач, не сводящихся к прямому применению алгоритма. Т.е.
те задачи, которые относятся к первой категории познавательной области: знание/понимание. В данной работе это прежде всего задания А4,
В8, В10, В11(!), С1, С3. Главная причина их неуспешного выполнения есть следствие методических «просчетов» учителя при организации
учебного процесса на уроке. Основная цель урока математики – это не разучивание решений задач определенного типа, а работа по развитию
мышления учащихся.
4
III.
Анализ результатов выполнения заданий ДКР по II части
3.1. Результаты выполнения заданий
Процент правильных ответов
Порядковый
номер
задания
Обозначение
задания в
работе
19
С4
20
С5
21
С6
22
С7
23
С8
Содержание задания
Выполнять разложение многочленов
на
множители;
выполнять
тождественные
преобразования
рациональных выражений
Проводить
доказательные
рассуждения
при
решении
геометрических задач
Распознавать
арифметические
прогрессии;
решать
задачи
с
применением формулы общего члена
и суммы нескольких первых членов
Моделировать реальные ситуации на
языке алгебры, составлять уравнения
по условию задачи; исследовать
построенные
модели
с
использованием аппарата алгебры
Решать
практические
задачи,
связанные
с
нахождением
геометрических величин
Баллы
2
Углубленное
Итого
изучение
Др.учебн.
по
Лицеи Гимназии предметов
СОШ заведения Итого заданию
44%
32%
32%
24%
20%
30%
1
3
15%
24%
12%
18%
10%
16%
7%
10%
7%
10%
10%
16%
40%
2
3
23%
27%
20%
23%
16%
17%
11%
13%
15%
9%
17%
18%
33%
2
4
13%
5%
11%
2%
12%
1%
8%
0%
14%
1%
12%
2%
30%
3
4
2%
4%
1%
1%
1%
1%
0%
0%
0%
0%
1%
1%
3%
3
3%
1%
1%
0%
0%
1%
2%
5
3.3. Анализ выполнения II части
Задания этой части работы
являются заданиями повышенного и
высокого уровня сложности. Степень
и качество выполнения заданий II
части
дают
возможность
дифференцировать
хорошо
успевающих школьников по уровням
подготовки,
выявить
наиболее
подготовленную часть выпускников,
в
частности,
составляющих
потенциал профильных классов.
Обращает на себя внимание тот
факт, что учащиеся более или менее
успешно
справляются
с
«алгоритмической»
частью
этих
заданий (в том числе и учащиеся
лицеев и классов с углубленным
изучением математики) и весьма
незначительная их часть может
математически грамотно и ясно
записать их решения, приводя при
этом необходимые пояснения и
обоснования (что является одним из
важнейших критериев при оценке
правильности выполнения заданий
этой части работы). Это свидетельствует о том, что учителя в повседневной практике преподавания основное внимание уделяют овладению
учащимися формально-оперативным алгебраическим аппаратом, пренебрегая при этом всеми другими аспектами обучения математики.
Как видно из приведенной выше таблицы (и диаграммы), процент выполнения заданий второй части понижается пропорционально
увеличению уровня сложности задания.
6
IV.
Общие результаты выполнения ДКР
4.1 Таблица количества участников ДКР
Район
Адмиралтейский
Василеостровский
Выборгский
Калининский
Кировский
Колпинский
Красногвардейский
Красносельский
Кронштадтский
Курортный
Московский
Невский
Петроградский
Петродворцовый
Приморский
Пушкинский
Фрунзенский
Центральный
Итого
Количество
ОУ
13
18
28
40
18
16
25
28
7
11
11
30
16
13
36
17
29
17
373
Количество учащихся
399
317
836
1398
461
264
642
536
308
330
504
564
390
309
854
374
751
538
10091
7
4.2. Результаты выполнения ДКР (в процентах). Данные о средней отметке и среднем тестовом балле
количество ОУ
количество учащихся
кол-во учащихся, набравших менее 8
баллов
кол-во учащихся, набравших 8 - 15 баллов
кол-во учащихся, набравших 16 -19 баллов
кол-во учащихся, набравших 20 - 34 балла
средний балл
средняя отметка
Углубленное
Др.учебн.
Лицеи Гимназии изучение предметов
СОШ
заведения Итого
38
55
80
188
11
1189
1556
2092
2080
3852
195
10091
6%
35%
25%
34%
15,9
3,9
10%
43%
24%
23%
14,9
3,6
11%
47%
23%
19%
14,2
3,5
20%
50%
19%
11%
8,3
3,2
22%
48%
18%
12%
12,1
3,2
13%
45%
23%
20%
13,5
3,5
Результаты выполнения ДКР 2012 вполне
соответствуют их распределению по типам ОУ, а
значит по уровню подготовки учащихся и их мотивации
к обучению вообще и математике в частности.
8
V.
Методические рекомендации
На этапе подготовки к итоговой аттестации следует заниматься не столько повторением «вообще», сколько сконцентрировать внимание
на тех вопросах, которые вызывают наибольшие затруднения у учащихся. В этот период, как никогда, необходим дифференцированный
подход.
При подготовке к выполнению I части работы особое внимание следует уделить формированию навыков самоконтроля, проверке ответа
на правдоподобие, на критическую оценку результатов.
При подготовке к выполнению II части работы необходимо обращать внимание учащихся на точность и полноту приводимых
обоснований.
В кодификаторе элементов содержания и требования к уровню подготовки обучающихся, освоивших основные общеобразовательные
программы основного общего образования, для проведения в 2012 году государственной (итоговой) аттестации (в новой форме) по математике
указано, что учащийся должен умет:
 моделировать практические ситуации и исследовать построенные модели с использованием аппарата алгебры.
 уметь перейти от словесной формулировки соотношений между величинами к алгебраической.
 проводить доказательные рассуждения при решении задач, выстраивать аргументацию при доказательстве, записывать
математические рассуждения, доказательства.
Мы много говорим о необходимости развития у учащихся навыков устной и письменной математической речи, о необходимости
формирования осознанности знаний учащихся, однако, никогда ранее при выполнении аттестационной работы эти умения и навыки никак не
учитывались, не проверялись и не оценивались. Теперь же это один из важных критериев, который оказывает существенное влияние на
итоговую оценку, определяющий уровень компетентности учащихся.
Немаловажную роль играет и психологическая подготовка учащихся, их собранность, настрой на успешное выполнение каждого из
заданий работы. Не следует стремиться выполнить I часть работы за более короткое время. В первую очередь это касается «сильных»
учащихся. Каким бы легким не казалось учащимся то или иное задание, к его выполнению следует относиться предельно серьезно. Именно
поспешность наиболее часто приводит к появлению неточностей, описок и т.п., а значит, и к неверному ответу на вопрос задачи.
Зав. кафедрой ФМО СПбАППО
Лукичева Е.Ю.
9