Домашнее задание № 3.2 Определить переходную и
реклама
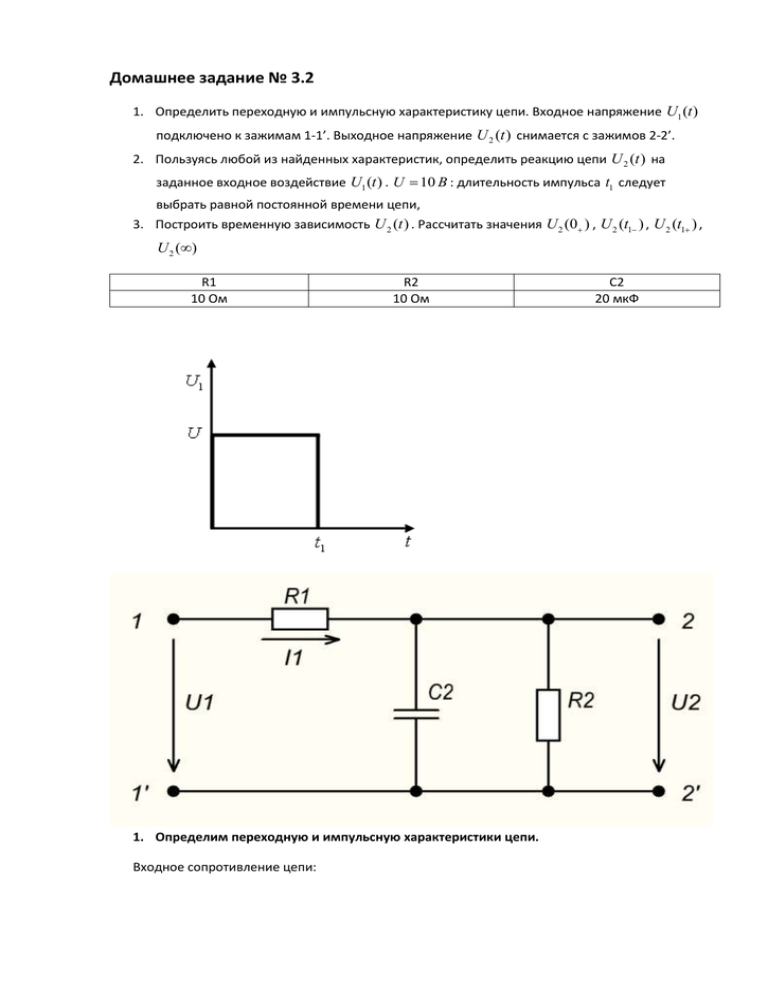
Домашнее задание № 3.2 1. Определить переходную и импульсную характеристику цепи. Входное напряжение U1 (t ) подключено к зажимам 1-1’. Выходное напряжение U 2 (t ) снимается с зажимов 2-2’. 2. Пользуясь любой из найденных характеристик, определить реакцию цепи U 2 (t ) на заданное входное воздействие U1 (t ) . U 10 В : длительность импульса t1 следует выбрать равной постоянной времени цепи, 3. Построить временную зависимость U 2 (t ) . Рассчитать значения U 2 (0 ) , U 2 (t1 ) , U 2 (t1 ) , U 2 () R1 10 Ом R2 10 Ом 1. Определим переходную и импульсную характеристики цепи. Входное сопротивление цепи: C2 20 мкФ 1 C2 p R2 R R2 R1 R2C2 p Z вх ( p) R1 R1 1 1 R2C2 p 1 R2C2 p 1 R2 C2 p R2 Ток I1 ( p ) равняется: I1 ( p ) U1 ( p ) R2C2 p 1 U1 ( p ) Z вх ( p ) R1 R2 R1 R2C2 p Выходное напряжение найдём по второму закону Кирхгофа: U 2 ( p ) U1 ( p ) I1 ( p ) R1 U1 ( p ) U1 ( p ) U1 ( p ) R2C2 p 1 R1 R1 R2 R1 R2C2 p R1 R2 R1 R2C2 p R1 R2C2 p R1 R2 U1 ( p ) R1 R2 R1 R2C2 p R1 R2 R1 R2C2 p Тогда передаточная функция цепи: W ( p) U 2 ( p) R2 U1 ( p ) R1 R2 R1 R2C2 p Подставляя числовые значения, получим: W ( p) U 2 ( p) 10 U1 ( p ) 20 0.002 p Переходная характеристика цепи h(t ) - это реакция цепи на единичное входное воздействие: 0, t 0 1(t ) 1, t 0 Изображение единичной функции 1 , поэтому мы можем найти изображение выходного p напряжение при таком воздействии на входе цепи: U 21 ( p) W ( p) 1 10 p p(20 0.002 p) Теперь найдём оригинал этого изображения выходного напряжения – это и будет переходная характеристика цепи. Изображение имеет вид дроби N ( p) , где корни уравнения M ( p ) 0 M ( p) равняются p1 0 c 1 и p2 104 c 1 . Повторяющихся корней нет. Производная знаменателя: M '( p) 20 0.004 p Так как дробь N ( p) мы можем представить в виде дроби: M ( p) N ( p) m N ( pk ) 1 M ( p) k 1 M '( pk ) p pk То в нашем случае: M '(0) 20 M ' 104 20 0.002 104 20 N (0) N 104 10 Таким образом: U 21 ( p) 10 0.5 0.5 p(20 0.002 p) p p 104 Оригинал U 21 ( p) , который и будет переходной функцией, имеет вид: h(t ) 0.5 1 e 10000t Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие, представляющее собой дельта-функцию (t ) . Изображение дельта-функции равняется 1, поэтому изображение выходного напряжения имеет вид: U 2 ( p) W ( p) 1 10 5 103 20 0.002 p p 104 Оригинал этого напряжения будет импульсной характеристикой цепи: h (t ) 5 103 e10000t Импульсная характеристика - это производная от переходной характеристики: h (t ) dh d 0.5(1 e 10000t ) 5 103 e 10000t dt dt 2. Определим реакцию цепи U 2 (t ) на заданное входное воздействие. Входное воздействие имеет вид: Где t1 - постоянная времени цепи. Постоянная времени цепи определяет время, в течении которого напряжение на выходе уменьшается в e раз. В нашем случае t1 1 104 с 4 10 Это входное воздействие можно рассматривать как 3 следующих друг за другом этапа: - скачок входного напряжения в момент времени 0 от 0 до U 10 В - постоянное значение U1 (t ) U 10 В при 0 t1 - скачок входного напряжения в момент времени t1 от U 10 В до 0 Воспользуемся для определения реакции цепи (нахождения U 2 (t ) ) интегралом Дюамеля: при 0 t 104 c : t1 U 2 (t ) (U 0)h(t ) 0 h(t )d 5 5e10 4 t 0 Первое слагаемое обусловлено скачком в момент времени 0 , второе слагаемое постоянным значением напряжения на входе цепи в период времени 0 t1 , равняется 0, так как U1 '(t ) 0 . при t 104 c t1 U 2 (t ) (U 0)h(t ) 0 h(t )d (0 U )h(t t1 ) 5e 10 t 5e 10 4 4 ( t 104 ) 0 Третье слагаемое обусловлено скачком напряжения в момент t1 . Воспользовавшись единичной функцией 1(t ) , можем записать для t 0 : U 2 (t ) 5 5e10 t 5 1 t 104 5e10 4 4 ( t 104 ) 1t 104 Входной сигнал имеет вид: 0, t 0 U1 (t ) U , 0 t t1 0, t t 1 U1 (t ) U 1(t ) 1(t t1 ) Найдём изображение входного напряжения U1 (t ) : U1 ( p) 4 U U 104 p 10 e 1 e10 p p p p Определим реакцию цепи на такое входное воздействие. Изображение выходного напряжения U 2 ( p) : 4 1 e 10 p 10 10 104 p 4 U 2 ( p ) W ( p )U1 ( p ) 1 e 5 10 20 0.002 p p p p 104 Рассмотрим дробь: N ( p) 1 M ( p ) p p 104 Корни уравнения M ( p ) 0 , откуда p1 0 и p2 104 . Первая производная M '( p) 2 p 104 . Таким образом: N (0) N (104 ) 1 M '(0) 104 M '(104 ) 104 1 104 104 p p 104 p p 104 Таким образом: 1 e U ( p) 5 10 4 2 104 p 5 p p 104 p 5 5 104 p 5 104 p e e p 104 p p 104 Оригинал выходного напряжения имеет вид: U 2 (t ) 5 5e10 t 5 1(t 104 ) 5e10 4 4 ( t 104 ) 1(t 104 ) Что совпадает с выходным напряжением, полученным с использованием переходной характеристики цепи. 3. Построим графически зависимость U 2 (t ) . Рассчитаем значения U 2 (0 ) , U 2 (t1 ) , U 2 (t1 ) , U 2 () График напряжения U 2 (t ) : Рассчитаем значения U 2 (t ) в моменты времени t 0 , t1 , t1 , . Для этого воспользуемся аналитическим выражением для U 2 (t ) . U 2 (t ) 5 5e10 t 5 1(t 104 ) 5e10 4 4 ( t 104 ) 1(t 104 ) Для t 0 : U 2 (0) 5 5 0 В Так как выходное напряжение – это напряжение на конденсаторе, поэтому согласно законам коммутации оно не может измениться скачком, а для t 0 оно было равно нулю, так как входное напряжение было равно нулю. Таким образом, U (0 ) U (0 ) 0 В . Для моментов времени t t1 и t t1 также U (t1 ) U (t1 ) , потому что выходное напряжение – это напряжение на конденсаторе, и оно не может измениться скачком, согласно законам коммутации. 4 U (t1 ) U (t1 ) U (104 ) 5 5e 10 10 5 1(104 104 ) 5e 10 4 4 (10 4 10 4 ) 1 5 1 3.16 В e Заметим, что, если бы входное напряжение представляло собой единичный скачок амплитудой U 10 В бесконечной длительности, то напряжение на конденсаторе для t равнялось бы напряжению на резисторе R2 в установившемся процессе: U Cm U R2 5 В . Но так как длительность единичного импульса ограниченно R1 R2 временем t1 , равным постоянной времени цепи, то конденсатор не успевает зарядиться до этого значения, и успевает зарядиться только до значения, на U Cm меньшее, а при t t1 e разряжается через резистор R2 . Для t : U 2 ( ) 5 5 0 В При t входное напряжение равняется нулю, поэтому при t t1 конденсатор разряжается через резистор R2 и напряжение на нем, которое равняется выходному, стремится к нулю. Ответ: Переходная характеристика цепи: h(t ) 0.5 1 e 10000t Импульсная характеристика цепи: h (t ) 5 103 e10000t Реакция цепи U 2 (t ) на заданное входное воздействие: U 2 (t ) 5 5e10 t 5 1(t 104 ) 5e10 4 U 2 (0) 0 В U (t1 ) U (t1 ) 3.16 В U 2 () 0 В 4 ( t 104 ) 1(t 104 )