Моделирование и компьютерный эксперимент

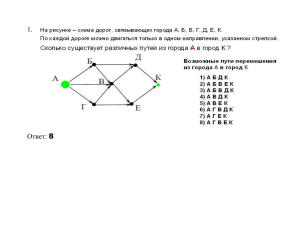
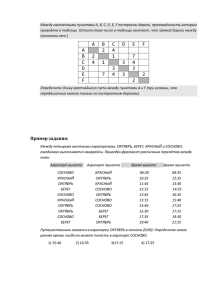
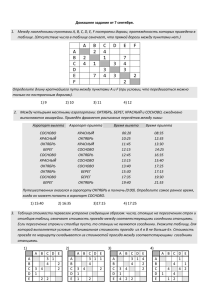
Задания для самостоятельной работы по теории и методике обучения информатике
Тема № 5
Моделирование и компьютерный эксперимент
Что нужно знать.
Модель — это упрощенное подобие реального объекта. Модель отражает лишь
некоторые свойства объекта, существенные с точки зрения цели моделирования
Модель — любой аналог, образ (изображение, описание, схема, символ, формула,
чертеж, график, план, карта, табли¬ца и т.п.) какого-либо объекта исследования.
Модель сохраняет наиболее важные и существенные для цели исследования
характеристики и свойства оригинала.
Один и тот же объект может иметь множество моделей.
Модель необходима для того, чтобы:
 понять, как устроен реальный объект;
 научиться управлять объектом или процессом;
 прогнозировать прямые или косвенные последствия реализации заданных
способов и форм воздействия на объект.
Моделирование — построение и изучение моделей с целью получения новых знаний,
научного познания объективного мира или дальнейшего совершенствования
характеристик объекта исследования.
В процессе классификации объектов часто строятся модели, которые имеют
иерархическую структуру. Группы объектов, обладающих одинаковыми общими
свойствами, называются классами объектов. Внутри класса объектов могут быть
выделены подклассы, объекты которых обладают некоторыми особенными свойствами, в
свою очередь подклассы могут делиться на еще более мелкие группы и так далее. Такой
процесс систематизации объектов называется процессом классификации.
Классификация моделей.
По области использования:
 игровые;
 имитационные;
 научно-технические;
 опытные;
 учебные.
С учетом фактора времени:
 статические;
 динамические;
 дискретные;
 непрерывные.
По области знаний:
 биологические;
 исторические;
 математические;
 социологические и т.п.
По способу представления:
 натурные (материальные);
 информационные.
В информационной модели отражаются знания человека об объекте моделирования.
Информационная модель — это описание в той или иной форме объекта моделирования.
Информационные модели делятся на описательные и формальные.
Описательные информационные модели — это модели, созданные на естественном
языке (т.е. на языке общения между людьми) в устной или письменной форме.
1
Задания для самостоятельной работы по теории и методике обучения информатике
Формальные информационные модели — это модели, созданные на формальном
языке (т.е. научном, профессиональном или программирования). Примеры формальных
моделей: все виды формул, таблицы, графы, карты, схемы и т.д.
По форме представления:
 геометрические;
 компьютерные;
 логические;
 математические;
 словесные;
 специальные;
 структурные и т.п.
Большую часть моделей, которыми пользуется человек, принято называть
системами.
Система — это целое, состоящее из элементов, взаимосвязанных между собой.
Однако связи элементов создают систему только тогда, когда образуют новый целостный
объект, обладающий свойствами, которые не были присущи просто совокупности данных
элементов.
Систематизация (классификация) — процесс превращения множества объектов в
систему.
Структура системы — определенный порядок объединения элементов системы.
Структурные информационные модели:
 алгоритмы;
 иерархические;
 сетевые;
 схемы (графы);
 табличные.
Рассмотрим подробнее самые значительные из них.
Табличной информационной моделью является прямоугольная таблица, которая
состоит из столбцов и строк. Такой тип моделей применяется для описания ряда объектов,
обладающих одинаковыми наборами свойств. Это один из наиболее используемых типов
информационных моделей.
В иерархической информационной модели объекты распределены по уровням.
Каждый элемент более высокого уровня может состоять из элементов нижнего уровня, а
элемент нижнего уровня может входить в состав только одного элемента более высокого
уровня.
Сетевые информационные модели применяются для отражения систем со сложной
структурой, в которых связи между элементами имеют произвольный характер.
Например, это различные региональные части глобальной компьютерной сети Интернет.
Компьютерные модели — это модели, реализованные на компьютере средствами
программного обеспечения.
Компьютерные модели:
 текст;
 графика;
 таблицы;
 звук;
 алгоритмы.
Основные этапы моделирования на компьютере:
 Построение модели.
 Формализация модели.
 Построение компьютерной модели.
2
Задания для самостоятельной работы по теории и методике обучения информатике
 Проведение компьютерного эксперимента.
 Анализ результатов моделирования.
В заданиях ЕГЭ встречаются задачи на сравнение табличной формы моделей и
моделей в виде схем, которые описывают один объект.
Примеры заданий.
Пример 1.
Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО,
ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов
между ними:
Аэропорт вылета Аэропорт прилета
СОСНОВО
КРАСНЫЙ
ОКТЯБРЬ
БЕРЕГ
СОСНОВО
КРАСНЫЙ
ОКТЯБРЬ
ОКТЯБРЬ
СОСНОВО
БЕРЕГ
КРАСНЫЙ
ОКТЯБРЬ
КРАСНЫЙ
СОСНОВО
ОКТЯБРЬ
СОСНОВО
СОСНОВО
БЕРЕГ
БЕРЕГ
ОКТЯБРЬ
Время вылета
Время прилета
06:20
10:25
11:45
12:15
12:45
13:15
13:40
15:30
17:35
19:40
08:35
12:35
13:30
14:25
16:35
15:40
17:25
17:15
19:30
21:55
Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите
самое раннее время, когда он может попасть в аэропорт СОСНОВО.
1) 15:40
2) 16:35
3)17:15
4) 17:25
Решение:
1) сначала заметим, что есть прямой рейс из аэропорта ОКТЯБРЬ в СОСНОВО с
прибытием в 17:25:
ОКТЯБРЬ
СОСНОВО
13:40
17:25
2) посмотрим, сможет ли путешественник оказаться в СОСНОВО раньше этого
времени, если полетит через другой аэропорт, с пересадкой
3) можно лететь, через КРАСНЫЙ, но, как следует из расписания,
ОКТЯБРЬ
КРАСНЫЙ
11:45
13:30
…
КРАСНЫЙ
СОСНОВО
13:15
15:40
путешественник не успеет на рейс КРАСНЫЙ – СОСНОВО, который улетает в
13:15, то есть на 15 минут раньше, чем в КРАСНЫЙ прилетает самолет
ОКТЯБРЬ – КРАСНЫЙ
4) можно лететь через БЕРЕГ,
БЕРЕГ
СОСНОВО
12:15
14:25
…
ОКТЯБРЬ
БЕРЕГ
15:30
17:15
но рейс БЕРЕГ – СОСНОВО вылетает даже раньше, чем рейс ОКТЯБРЬ –
БЕРЕГ, то есть, пересадка не получится
3
Задания для самостоятельной работы по теории и методике обучения информатике
5) поскольку даже перелеты с одной пересадкой не стыкуются по времени,
проверять варианты с двумя пересадками в данной задаче бессмысленно (хотя в
других задачах они теоретически могут дать правильное решение)
6) таким образом, правильный ответ – 4 (прямой рейс).
Пример 2.
В таблице приведена стоимость перевозок между соседними железнодорожными
станциями. Укажите схему, соответствующую таблице.
Решение:
Представим значения отрезков линий в виде четырех таблиц:
Анализируя полученную таблицу, можно сделать вывод, что только чертеж № 2
удовлетворяет представленной таблице.
4
Задания для самостоятельной работы по теории и методике обучения информатике
Пример 3.
Таблица стоимости перевозок устроена следующим образом: числа, стоящие на
пересечениях строк и столбцов таблиц, означают стоимость проезда между
соответствующими соседними станциями. Если пересечение строки и столбца пусто, то
станции не являются соседними.
Укажите таблицу, для которой выполняется условие: «Минимальная стоимость
проезда из А в B не больше 6».
Решение:
Стоимость проезда по маршруту складывается из стоимостей проезда между
соответствующими соседними станциями.
В этой задаче необходимо сделать модель перевозок в виде схемы для каждой из
четырех таблиц, а затем подсчитать стоимость проезда.
Рассмотрим алгоритм построения схемы на примере третьей таблицы.
Имеется станция А, которая связана со станциями C и D.
Станция D не связана ни с одной станцией, кроме A. Станция C, кроме станции A,
связана еще со станциями B и E.
Из дальнейшего анализа таблицы видно, что станции B и E связаны между собой:
Теперь подсчитаем стоимость обоих возможных путей:
ACB = 3 + 4 = 7
ACEB = 3 + 2 + 1 = 6
Второй вариант подходит под условие задачи.
5
Задания для самостоятельной работы по теории и методике обучения информатике
Аналогично можно нарисовать схему по любой таблице и наоборот.
Пример 4.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
Д
Б
А
И
Ж
В
Г
К
Е
Решение:
1) начнем считать количество путей с конца маршрута – с города К
2) будем обозначать через NX количество различных путей из города А в город X
3) общее число путей обозначим через N
4) по схеме видно, что NБ = NГ = 1
5) очевидно, что если в город X можно приехать только из Y, Z, то NX = NY + NZ,
то есть нужно сложить число путей, ведущих из A во все города, откуда можно
приехать в город X
6) поскольку в K можно приехать из Е, Д, Ж или И, поэтому
N = NК = NД + NЕ + NЖ + NИ
7) в город И можно приехать только из Д, поэтому NИ = NД
8) в город Ж можно приехать только из Е и В, поэтому
NЖ = NЕ + NВ
9) подставляем результаты пп. 6 и 7 в формулу п. 5:
N = NВ + 2NЕ + 2NД
10) в город Д можно приехать только из Б и В, поэтому
NД = NБ + NВ
так что
N = 2NБ + 3NВ + 2NЕ
11) в город Е можно приехать только из Г, поэтому NЕ = NГ так что
N = 2NБ + 3NВ + 2NГ
12) по схеме видно, что NБ = NГ = 1, кроме того, NВ = 1 + NБ + NГ = 3
13) окончательно N = 2NБ + 3NВ + 2NГ = 2·1 + 3·3 + 2·1 = 13
14) Ответ: 13.
Задания для самостоятельной работы.
1. Между четырьмя крупными аэропортами, обозначенными кодами СЕВЕРНЫЙ,
ЮЖНЫЙ, ЗАПАДНЫЙ и ВОСТОЧНЫЙ, ежедневно выполняются авиарейсы.
Приведен фрагмент расписания перелетов между этими аэропортами.
6
Задания для самостоятельной работы по теории и методике обучения информатике
Путешественник находится в аэропорту ЮЖНЫЙ в полночь (0:00). Определите
самое раннее время, когда он может оказаться в аэропорту ЗАПАДНЫЙ.
1) 18:30
2) 17:30
3) 15:20
4) 14:30.
2. Между четырьмя крупными железнодорожными станциями, обозначенными кодами
СЕРОВО, МУЛИНО, ПЕР- ВАК и ДОЛИНА, ежедневно выполняются
железнодорожные переезды. Приведен фрагмент расписания переездов между этими
станциями.
Путешественник находится на станции СЕРОВО в полночь (0:00). Определите самое
раннее время, когда он может оказаться на станции ДОЛИНА.
7
Задания для самостоятельной работы по теории и методике обучения информатике
1)
2)
3)
4)
13:20
14:40
16:20
18:30.
3. Путешественник пришел в 08:00 на автостанцию поселка ЛЕСНОЕ и увидел следующее
расписание автобусов:
Отправление из
прибытия
Прибытие в
Время отправления
Время
ЛЕСНОЕ
ОЗЕРНОЕ
07:45
08:55
ЛУГОВОЕ
ЛЕСНОЕ
08:00
09:10
ПОЛЕВОЕ
ЛЕСНОЕ
08:55
11:25
ПОЛЕВОЕ
ЛУГОВОЕ
09:10
10:10
ЛЕСНОЕ
ПОЛЕВОЕ
09:15
11:45
ОЗЕРНОЕ
ПОЛЕВОЕ
09:15
10:30
ЛЕСНОЕ
ЛУГОВОЕ
09:20
10:30
ОЗЕРНОЕ
ЛЕСНОЕ
09:25
10:35
ЛУГОВОЕ
ПОЛЕВОЕ
10:40
11:40
ПОЛЕВОЕ
ОЗЕРНОЕ
10:45
12:00
Определите самое раннее время, когда путешественник сможет оказаться в пункте
ПОЛЕВОЕ согласно этому расписанию.
1) 10:30
2) 11:25
3)11:40
4) 11:45
4. Путешественник пришел в 08:00 на автостанцию поселка КАЛИНИНО и увидел
следующее расписание автобусов:
Отправление из
прибытия
КАМЫШИ
КАЛИНИНО
РАКИТИНО
РАКИТИНО
РАКИТИНО
КАЛИНИНО
КАЛИНИНО
БУКОВОЕ
КАМЫШИ
БУКОВОЕ
Прибытие в
КАЛИНИНО
БУКОВОЕ
КАМЫШИ
КАЛИНИНО
БУКОВОЕ
РАКИТИНО
КАМЫШИ
КАЛИНИНО
РАКИТИНО
РАКИТИНО
Время отправления
08:15
09:10
10:00
10:05
10:10
10:15
10:20
10:35
11:25
11:40
Время
09:10
10:15
11:10
12:25
11:15
12:35
11:15
11:40
12:30
12:40
Определите самое раннее время, когда путешественник сможет оказаться в пункте
РАКИТИНО согласно этому расписанию.
1) 12:25
2) 12:30
3)12:35
4) 12:40
5. Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА,
ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между
ними:
Аэропорт вылета Аэропорт прилета
ВОСТОРГ
ОЗЕРНЫЙ
ГОРКА
ЗАРЯ
8
Время вылета
Время прилета
13:10
13:00
17:15
14:30
Задания для самостоятельной работы по теории и методике обучения информатике
ОЗЕРНЫЙ
ГОРКА
ВОСТОРГ
ЗАРЯ
ВОСТОРГ
ЗАРЯ
ГОРКА
ОЗЕРНЫЙ
ВОСТОРГ
ОЗЕРНЫЙ
ОЗЕРНЫЙ
ОЗЕРНЫЙ
ЗАРЯ
ГОРКА
ЗАРЯ
ГОРКА
12:10
11:15
12:35
12:30
10:30
14:40
15:15
14:30
14:20
15:30
14:50
14:20
12:15
16:45
17:20
16:20
Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите
самое раннее время, когда он может попасть в аэропорт ГОРКА.
1) 13:10
2) 16:20
3)16:45
4) 17:15
6. Путешественник пришел в 08:00 на автостанцию поселка ОЛЬГИНО и увидел
следующее расписание автобусов:
Отправление из
прибытия
САВВИНО
ОЛЬГИНО
ПАВЛИНО
ОЛЬГИНО
ПАВЛИНО
ОЛЬГИНО
ПАВЛИНО
КУЧИНО
САВВИНО
КУЧИНО
Прибытие в
ОЛЬГИНО
ПАВЛИНО
КУЧИНО
КУЧИНО
САВВИНО
САВВИНО
ОЛЬГИНО
ПАВЛИНО
ПАВЛИНО
ОЛЬГИНО
Время отправления
07:10
07:30
07:50
09:15
09:15
09:30
09:30
10:10
11:05
11:30
Время
08:25
08:40
09:00
10:20
10:25
10:30
10:45
11:20
12:15
12:40
Определите самое раннее время, когда путешественник сможет оказаться в пункте
ПАВЛИНО согласно этому расписанию.
1) 08:40
2) 10:45
3)11:20
4) 12:15
7. Путешественник пришел в 08:00 на автостанцию поселка ЧЕРНОЕ и увидел
следующее расписание автобусов:
Отправление из
прибытия
СВЕТЛОЕ
КРАСНОЕ
ЧЕРНОЕ
ЧЕРНОЕ
КРАСНОЕ
ЧЕРНОЕ
ЛАЗАРЕВО
ЛАЗАРЕВО
СВЕТЛОЕ
КРАСНОЕ
Прибытие в
ЧЕРНОЕ
ЛАЗАРЕВО
КРАСНОЕ
ЛАЗАРЕВО
СВЕТЛОЕ
СВЕТЛОЕ
КРАСНОЕ
ЧЕРНОЕ
КРАСНОЕ
ЧЕРНОЕ
Время отправления
06:15
07:15
07:30
08:25
09:05
09:10
10:30
11:05
12:10
13:10
Время
08:55
09:45
11:40
10:45
10:25
11:50
13:00
13:45
13:25
17:25
Определите самое раннее время, когда путешественник сможет оказаться в пункте
КРАСНОЕ согласно этому расписанию.
9
Задания для самостоятельной работы по теории и методике обучения информатике
1) 11:40
2) 13:00
3)13:10
4) 13:25
8. Путешественник пришел в 08:00 на автостанцию поселка ЛИСЬЕ и увидел
следующее расписание автобусов:
Отправление из
прибытия
ЛИСЬЕ
СОБОЛЕВО
ЕЖОВО
ЗАЙЦЕВО
ЛИСЬЕ
ЛИСЬЕ
ЗАЙЦЕВО
СОБОЛЕВО
ЕЖОВО
ЗАЙЦЕВО
Прибытие в
Время отправления
ЗАЙЦЕВО
ЛИСЬЕ
ЛИСЬЕ
ЕЖОВО
СОБОЛЕВО
ЕЖОВО
ЛИСЬЕ
ЗАЙЦЕВО
ЗАЙЦЕВО
СОБОЛЕВО
07:50
08:55
09:05
10:00
10:15
10:45
11:05
11:10
12:15
12:45
Время
09:05
10:05
10:15
11:10
11:30
12:00
12:15
12:15
13:25
13:55
Определите самое раннее время, когда путешественник сможет оказаться в пункте
ЗАЙЦЕВО согласно этому расписанию.
1) 9:05
2) 12:15
3)12:25
4) 13:25
9. Транспортная фирма осуществляет грузоперевозки разными видами транспорта между
четырьмя городами: ЧЕРЕПОВЕЦ, МОСКВА, КУРСК, ПЕРМЬ. Стоимость доставки
грузов и время в пути указаны в таблице:
Пункт отправления Пункт назначения
МОСКВА
МОСКВА
МОСКВА
ПЕРМЬ
ЧЕРЕПОВЕЦ
ЧЕРЕПОВЕЦ
ЧЕРЕПОВЕЦ
КУРСК
КУРСК
КУРСК
КУРСК
Стоимость (у.е.)
ПЕРМЬ
КУРСК
ЧЕРЕПОВЕЦ
МОСКВА
ПЕРМЬ
МОСКВА
КУРСК
ПЕРМЬ
МОСКВА
ЧЕРЕПОВЕЦ
ЧЕРЕПОВЕЦ
100
30
50
100
140
50
100
60
30
100
90
Время в пути
70
10
15
69
80
15
80
40
10
80
100
Определите маршрут наиболее дешевого варианта доставки груза из ЧЕРЕПОВЦА в
ПЕРМЬ. Если таких маршрутов несколько, в ответе укажите наиболее выгодный по
времени вариант.
1) ЧЕРЕПОВЕЦ – ПЕРМЬ
2) ЧЕРЕПОВЕЦ – КУРСК – ПЕРМЬ
3) ЧЕРЕПОВЕЦ – МОСКВА – ПЕРМЬ
4) ЧЕРЕПОВЕЦ – МОСКВА – КУРСК – ПЕРМЬ
10. Турист-паломник должен добраться из МУРМАНСКА в КИЕВ. Автобусная компания
предложила ему следующий список маршрутов, которые проходят через города:
МУРМАНСК, КИЕВ, МОСКВУ и СМОЛЕНСК.
10
Задания для самостоятельной работы по теории и методике обучения информатике
Пункт отправления Пункт прибытия
монастырей
МУРМАНСК
МУРМАНСК
МУРМАНСК
МОСКВА
МОСКВА
МОСКВА
СМОЛЕНСК
СМОЛЕНСК
КИЕВ
КИЕВ
КИЕВ
Стоимость (у.е.)
КИЕВ
МОСКВА
СМОЛЕНСК
КИЕВ
МУРМАНСК
СМОЛЕНСК
КИЕВ
МОСКВА
МОСКВА
СМОЛЕНСК
МУРМАНСК
200
100
110
60
100
20
40
30
60
35
190
Число
81
10
30
7
9
15
15
15
7
10
37
В таблице путешественник указал для себя количество монастырей, мимо которых
будет проезжать автобус. Помогите путешественнику добраться в пункт назначения,
затратив на дорогу не более 190 у.е. и увидев максимальное количество
монастырей. В ответе укажите маршрут паломника:
1) МУРМАНСК – СМОЛЕНСК – КИЕВ
2) МУРМАНСК – МОСКВА – КИЕВ
3) МУРМАНСК – МОСКВА – СМОЛЕНСК – КИЕВ
4) МУРМАНСК – СМОЛЕНСК – МОСКВА – КИЕВ
11. В таблице приведена стоимость перевозок между соседними железнодорожными
станциями. Укажите схему, соответствующую таблице.
11
Задания для самостоятельной работы по теории и методике обучения информатике
12. В таблице приведена стоимость перевозок между соседними железнодорожными
станциями. Укажите схему, соответствующую таблице.
13. В таблице приведена стоимость
станциями. Укажите схему,
A
A
B 4
C
D 5
1)
2)
перевозок между соседними железнодорожными
соответствующую таблице.
B C D
4
5
3 6
3
6
3)
4)
14. В таблице приведена стоимость перевозки пассажиров между соседними населенными
пунктами. Укажите схему, соответствующую таблице.
A
B
C
D
1)
A
B
1
2
2
3
2)
12
C
1
2
5
3)
D
2
3
5
4)
Задания для самостоятельной работы по теории и методике обучения информатике
3
5
D
2
B
2
1
A
1
С
B
C
A
5
3
D
1
2
1
2
B
5
D
3
C
5
A
2
A
С
2
3
1
B
D
15.
В таблице приведена стоимость перевозки пассажиров между соседними
населенными пунктами. Укажите схему, соответствующую таблице.
A
A
B
C
D
1)
B
3
C
3
2
2
1
1
4
2)
2
D
B
1
1
4
A
3)
4)
C
A
1
С
D
1
1
4
4
3
D
1
1
2
B
A
С
B
B
3
2
3
2
1
4
C
1
A
4
D
D
16.
В таблице приведена стоимость перевозки пассажиров между соседними
населенными
пунктами.
Укажите схему, соответствующую
таблице.
A B C D E
A
1 4
1
B 1
2
C 4 2
3
D
3
E 1
1)
2)
4
3
E
1
A
4
B
1
3
D
1
3
1
2
C
B
2
B
E
B
1
E
С
4
D
С
4)
A
1
A
3)
2
D
2
1
A
D
1
4
C
3
E
17. В таблице приведена стоимость перевозки пассажиров между соседними населенными
пунктами. Укажите схему, соответствующую таблице.
A
A
B
B
2
C
4
2
13
D
1
E
Задания для самостоятельной работы по теории и методике обучения информатике
C
D
E
1)
4
1
5
4
5
2)
2
A
4
1
D
B
C
5
4
3)
4
4
E
C
E
5
A
1
4)
5
D
B
4
E
2
4
D
C
E
4
5
C
A
4
1
2
B
4
A
2
D
1
B
18. В таблице приведена стоимость перевозки пассажиров между соседними населенными
пунктами. Укажите схему, соответствующую таблице.
19.
В таблице приведена стоимость перевозки пассажиров между соседними
населенными пунктами. Укажите схему, соответствующую таблице.
14
Задания для самостоятельной работы по теории и методике обучения информатике
20. В таблице приведена стоимость перевозки пассажиров между соседними населенными
пунктами. Укажите схему, соответствующую таблице.
A
A
B
C
D
1)
1
B
1
A
4
C
3
С
1
4
3)
C
A
1
D
D
1
1
4
2
2
1
2)
2
D
B
3
4
3
1
B
3
1
2
С
A
4)
2
4
B
B
2
3
1
A
1
D
C
4
D
21. Таблица стоимости перевозок устроена следующим обра¬зом: числа, стоящие на пресечениях
строк и столбцов таблиц, означают стоимость проезда между соответству¬ющими соседними
станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в
В не больше 6». Стоимость проезда по маршруту складывается из стои¬мостей проезда между
соответствующими соседними станциями.
Стоимость проезда по маршруту складывается из стоимостей проезда между
соответствующими соседними станциями.
15
Задания для самостоятельной работы по теории и методике обучения информатике
22. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях
строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними
станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в
B не больше 6».
Стоимость проезда по маршруту складывается из сто¬имостей проезда между
соответствующими соседними станциями.
23. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях
строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними
станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в
B не больше 6».
Стоимость проезда по маршруту складывается из стоимостей проезда между
соответствующими соседними станциями.
16
Задания для самостоятельной работы по теории и методике обучения информатике
24. В таблицах приведена протяженность автомагистралей между соседними
населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие
населенные пункты не соединены автомагистралями. Укажите номер таблицы, для
которой выполняется условие «Максимальная протяженность маршрута от пункта А до
пункта С не больше 5». Протяженность маршрута складывается из протяженности
автомагистралей между соответствующими соседними населенными пунктами. При
этом любой населенный пункт должен встречаться на маршруте не более одного раза.
1)
2)
A
B
C
D
A B C D
2
2
2
1 3
1
3
2 3 3
3)
A
B
C
D
A B
2
2
2 1
1
C D
2
1 1
3
3
4)
A
B
C
D
A B C D
2 3 2
2
2 2
3 2
2 2
A
B
C
D
A B
3
3
2 2
1
C D
2 1
2
1
1
25. В таблице приведена стоимость перевозки грузов между соседними станциями. Если
пересечение строки и столбца пусто, то соответствующие станции не являются
соседними. Укажите таблицу, для которой выполняется условие «Минимальная
стоимость перевозки грузов от пункта А до пункта В не больше 3».
1)
2)
3)
4)
A B C D Е
A B C D Е
A B C D Е
A B C D Е
A
1
A
5 1
A
3 1 1
A
2 1 3
B
4
3
B
4
2
B
2 1
B
2
2
C
4
4
C 5 4
C 3 2
C 2 2
D 1
4
D 1
D 1 1
D 1
Е
3
Е
2
Е 1
Е 3 2
26. В таблицах приведена стоимость перевозки грузов между соседними станциями. Если
пересечение строки и столбца пусто, то соответствующие станции не являются
соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная
17
Задания для самостоятельной работы по теории и методике обучения информатике
стоимость перевозки грузов от пункта В до пункта D не больше 6».
1)
2)
3)
A B C D
A B C D
A B C D
A
2
2
A
2 1 1
A
1 3 6
B 2
4 3
B 2
4
B 1
2 4
C
4
4
C 1 4
1
C 3 2
D 2 3 4
D 1
1
D 6 4
4)
A
B
C
D
A B
3
3
2 2
1
C D
2 1
2
4
4
27. В таблицах приведена протяженность автомагистралей между соседними
населенными пунктами. Если пересечение строки и столбца пусто, то
соответствующие населенные пункты не являются соседними. Укажите номер
таблицы, для которой выполняется условие «Максимальная протяженность маршрута
от пункта А до пункта С не больше 6». Протяженность маршрута складывается из
протяженности автомагистралей между соответствующими соседними населенными
пунктами. При этом через любой насеченный пункт маршрут должен проходить не
более одного раза.
1)
2)
3)
4)
A B C D
A B C D
A B C D
A B C D
A
1
2
A
1 2
A
3 3 2
A
3 2 1
B 1
4 3
B 1
4 2
B 3
4 3
B 3
4
C
4
3
C 2 4
3
C 3 4
C 2 4
1
D 2 3 3
D
2 3
D 2 3
D 1
1
28. В таблицах приведена протяженность автомагистралей между соседними
населенными пунктами. Если пересечение строки и столбца пусто, то
соответствующие населенные пункты не являются соседними. Укажите номер
таблицы, для которой выполняется условие «Максимальная протяженность маршрута
от пункта C до пункта B не больше 6». Протяженность маршрута складывается из
протяженности автомагистралей между соответствующими соседними населенными
пунктами. При этом через любой насеченный пункт маршрут должен проходить не
более одного раза.
1)
2)
3)
4)
A B C D E
A B C D E
A B C D E
A B C D E
A
4 3
7
A
2 5
6
A
2 2 6
A
5 2
6
B 4
2
B 2
3
B
2
B 5
5
C 3
6
C 5
C 2
2
C 2
2
D
2 6
1
D
3
1
D 2 2 2
D
5 2
3
E 7
1
E 6
1
E 6
E 6
3
29. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги
между пунктами нет.)
A
A
B
C
D
E
B
5
5
9
3
8
C
D
E
9
3
8
4
2
4
2
18
F
7
Задания для самостоятельной работы по теории и методике обучения информатике
F
7
Определите длину кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
1) 11
2) 13
3) 15
4) 17
30. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость
которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги
между пунктами нет.)
A
A
B
C
D
E
F
B
4
4
6
3
6
C
D
E
6
3
6
4
2
4
2
F
5
5
Определите длину кратчайшего пути между пунктами A и F (при условии, что
передвигаться можно только по построенным дорогам).
1) 9
2) 13
3) 14
4) 15
31. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
Е
Б
А
Ж
В
К
З
Г
И
Д
32. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город З?
Д
Б
А
Е
В
З
Г
Ж
19
Задания для самостоятельной работы по теории и методике обучения информатике
33. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город З?
Д
Б
Е
В
А
З
Г
Ж
34. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
Е
Б
В
А
Ж
Г
К
З
И
Д
35. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город К?
Е
Б
В
А
Ж
Г
К
З
И
Д
36. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
20
Задания для самостоятельной работы по теории и методике обучения информатике
Е
Б
А
В
Ж
Г
К
З
И
Д
37. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
Е
Б
А
В
Ж
Г
К
З
И
Д
38. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
Е
Б
А
В
Ж
Г
К
З
И
Д
39. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
21
Задания для самостоятельной работы по теории и методике обучения информатике
Е
Б
В
А
К
Ж
Г
З
И
Д
40. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько
существует различных путей из города А в город Ж?
Е
Б
В
А
К
Ж
Г
З
И
Д
Варианты заданий.
Номер варианта
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Номера заданий
1, 11, 21, 31
2, 12, 22, 32
3, 13, 23, 33
4, 14, 24, 34
5, 15, 25, 35
6, 16, 26, 36
7, 17, 27, 37
8, 18, 28, 38
9, 19, 29, 39
10, 20, 30, 40
22