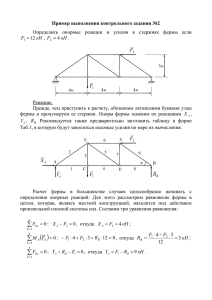
ЗАДАНИЕ 1. Определение реакций опор и сил в стержнях... фермы Определить реакции опор фермы от заданной нагрузки, а также
реклама

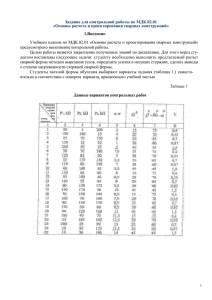
ЗАДАНИЕ 1. Определение реакций опор и сил в стержнях плоской фермы Определить реакции опор фермы от заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов. Схемы ферм показаны на рис. 1.0 – 1.9. Необходимые для расчета данные приведены в таблице 1. Дополнительно определить силы в стержнях 1,2,3 фермы от той же нагрузки способом Риттера (способом сечений). ПРИМЕЧАНИЕ: Для построения фермы из табл. 1 выбираются только те размеры, которые указаны на рисунке Номер условия F1 0 1 F2 F3 ТАБЛИЦА 1 a h 4 8 kH 9 3 2 4 2 2 3 4 Град. 30 60 2 3 2 10 9 10 6 5 3 4 3 4 60 60 4 5 2 3 4 7 2 5 5 4 3 3 60 45 6 7 4 5 6 7 3 7 4 5 5 4 30 30 8 9 10 3 8 4 2 5 5 3 3 4 45 60 Рис. 1.0 м α Рис. 1.1 Рис. 1.2 Рис. 1.3 Рис. 1.4 Рис. 1.5 Рис. 1.6 Рис. 1.7 Рис. 1.8 Рис. 1.9 ПРИМЕР 1. Расчет плоской фермы. Дано: F1= 4 кН; F2=3 кН; а= 5 м. Определить: 1. Усилия S1-S9 в стержнях фермы методом вырезания узлов; 2. Усилия S2, S3 и S4 в стержнях фермы методом сечений. 1. Проведем расчет реакций опор фермы. Рассмотрим ферму, образованную из одинаковых равнобедренных треугольников. В этой ферме число узлов n = 6, а число стержней k = 9. k = 26 – 3 = 12 – 3 = 9 Ферма является жесткой и без лишних стержней. Отбросим связи и заменим их реакциями связей. Составим уравнения условия равновесия для полученной плоской системы сил. Fkx 0 Fky 0 mB Fk 0 F1 X B 0 R A F2 YB 0 R 2a F a 0 2 A Решая эти уравнения, найдем реакции в опорах. X B F1 4kH F2 a 3 1,5kH R A 2a 2 YB R A F2 1,5 3 1,5kH Для проверки правильности определения реакций опор составим уравнение моментов относительно точки М и подставим в него найденные значения реакций опор: YB a X B a F1 a RA a a(YB X B F1 RA ) a(1,5 4 4 1,5) 0 0≡0 Перейдем к определению усилий в стержнях. 2. Расчет усилий фермы по методу вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы этого пронумеруем все стержни. Искомые усилия будем обозначать S1, S2….Вырежем мысленно все узлы вместе со сходящимися в них стержнями и направим усилия в этих стержнях от узлов, считая все стержни растянутыми. Если в результате расчетов величина усилия в каком-либо стержне окажется отрицательной, это будет означать, что данный стержень сжат. Теперь для сил, сходящихся в каждом узле, составим уравнения равновесия. Fkx 0 Fky 0 Для проверки правильности определения усилий в стержнях, построим векторный многоугольник в масштабе F . F 4kH кН 0,1 40 мм мм Если многоугольник будет замкнут, то усилия найдены верно. Узел А Запишем условие равновесия системы сходящихся сил, приложенных к узлу А: Fkx 0 Fky 0 S 2 cos 0 R A S1 0 S2 0 S1 R A 1,5kH Знак «минус» означает, что стержень сжат. Узел С Fkx 0 Fky 0 S 3 0 S 4 S1 0 S3 0 S 4 S1 1,5kH Для проверки строим силовой многоугольник. Узел Е Fkx 0 Fky 0 F1 S 6 S 5 cos 0 S 4 S 5 sin 0 S4 1,5 2,12kH sin 0,707 S 6 F1 S 5 cos 4 2,12 0,707 5,5kH S5 Для проверки строим силовой четырехугольник. Узел D Fkx 0 Fky 0 S 6 S 8 0 S 7 F2 0 S 8 S 6 5,5kH S 7 F2 3kH Проведем графическую проверку. Узел В Fkx 0 Fky 0 S9 S 8 X B S 9 cos 0 YB S 9 sin 0 YB 1,5 2,12kH sin 0,707 Строим силовой четырехугольник. Узел М Для узла М все усилия определены, поэтому проведем только графическую проверку. Строим силовой треугольник. 5.3. Расчет плоских ферм методом сечений (методом Риттера). Идея метода состоит в том, что ферму рассекают на две части сечением, проходящим через три стержня, в которых требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направленными вдоль стержней в направлении от узлов к середине стержней, считая все стержни растянутыми. Затем составляем уравнения равновесия в виде суммы моментов всех сил относительно таких точек, чтобы в каждое уравнение входило только одно неизвестное усилие. Чтобы определить усилия в стержнях 4, 3, 2 составим следующие уравнения равновесия: m A Fk 0 mC Fk 0 m М Fk 0 S 3 0 S 2 0 S R 1,5kH A 4 S 3 a 0 S 2 a sin 0 S a R a 0 A 4 Если два неизвестных усилия параллельны какой-либо оси, то для нахождения третьего достаточно составить уравнение равновесия в проекции на ось, перпендикулярную первым двум силам.