Грыжов В.К., Корольков В.Г. г. Вязьма, Смоленская область
реклама

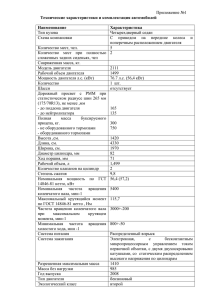
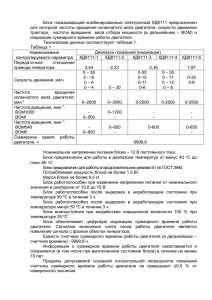
Грыжов В.К., Корольков В.Г. г. Вязьма, Смоленская область филиал ГОУ ВПО Московского государственного университета технологий и управления в г. Вязьме Смоленской области ИНФОРМАЦИОННО- МЕТОДИЧЕСКИЙ МОДУЛЬ ДЛЯ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ ИНЖЕНЕРНЫХ КАДРОВ ПО ДИСЦИПЛИНЕ: «ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ» Как известно, теория автоматического управления (ТАУ) является отраслью науки, в которой рассматриваются проблемы проектирования систем автоматического управления (САУ) техническими объектами и технологическими процессами вне зависимости от их физической природы. Принципиальное значение для методологии ТАУ имеет то, что САУ являются системами взаимодействующих между собой объекта управления и автоматического управляющего устройства (контроллера). Соответственно, основным подходом при изучении и проектировании таких систем должен быть системный подход. Этого можно достичь при использовании традиционного лабораторного практикума с реальными объектами управления и составляющими звеньями систем управления. При дистанционном образовании студент часто не имеет возможности доступа к реальным объектам. В этом случае большую помощь для развития практических навыков студентов может оказать применение компьютерных технологий. К настоящему времени имеется обширная монографическая и учебная литература по ТАУ. Целостного законченного комплекса практических и лабораторных работ для дистанционного образования фактически не существует. В Вяземском филиале МГУТУ к настоящему времени на базе среды моделирования VisSim разработаны и применяются в учебном процессе некоторые модели систем управления, в частности предлагаемый модуль. Для практической реализации этого модуля были решены следующие основные задачи: 1. В соответствии с учебной программой по дисциплине разработан краткий электронный конспект лекций, включающий список основной и дополнительной литературы, а также адреса разработок в Internet. 2. В соответствии с требования образовательных стандартов разработан комплекс лабораторных работ и практических занятий с примерами выполнения индивидуальных заданий в среде моделирования VisSim. 3. Разработаны методические указания и задания для курсового проектирования и контрольных работ. 4. Разработаны электронные тесты для промежуточного и итогового контроля знаний студентов. 5. Разработаны критерии анализа освоения материала и рекомендаций для дальнейшего обучения. Рассмотрим пример проведения и оформления одной лабораторной работы из семи, включенных в состав модуля. Название: «Исследование дискретных линейных систем управления». Цель лабораторной работы: разработать и исследовать цифровую систему автоматического управления электродвигателем постоянного тока с нагрузкой. 1. Постановка задачи. Описание звеньев системы. 1.1 Объект управления- двигатель постоянного тока независимого возбуждения, управляемый по цепи якоря, с нагрузкой. Передаточная функция ОУ задается: W ( p) ( p) U ( p) kД 1,5 p 1 , где k Д - передаточный коэффициент; ( p) - изображение по Лапласу угловой скорости вращения вала – выходной управляемой величины; U ( p ) - изображение входной величины- напряжения, подаваемого на цепь якоря. Нагрузочные характеристики двигателя (мощность М) приводятся на рисунке 1.1. , c 1 400 300 V4 70В V3 60 В V2 50В V1 40В 200 100 10 20 30 40 50 60 70 M,H м 80 Рис. 1.1. 1.2. На якорь двигателя подается постоянное напряжение, значение которого изменяется широтно-импульсным модулятором (ШИМ). Статическая характеристика ШИМ- регулирующего органа нелинейная, задана в виде таблицы , где Uвх- входное напряжение на ШИМ, Uвых- напряжение, подаваемое на двигатель. Таблица. 1 Uвх, В 1,5 2,0 2,5 3,0 3,5 Uвых, В 52 63 73 82 90 1.3. Скорость вращения вала двигателя измеряется с помощью тахогенератора, у которого массой и моментом инерции можно пренебречь. В таком случаи, тахогенератор является безынерционным звеном, у которого зависимость ЭДС от скорости пропорциональная: , где - передаточный коэффициент тахогенератора, 5,5 10 3 В * с. Его передаточная функция W ( p) U ( p) 5,5 10 3 . ( p) W ( p) - изображение входного сигнала; ( p) - угловой скорости вращения; U ( p ) - изображение входного напряжения. 1.4. Цифровой микроконтроллер должен реализовать дискретный ПИрегулятор. В состав микроконтроллера входит АЦП и ЦАП. Основные требования, предъявляемые к проектируемой системе управления: - погрешность регулирования выходной переменной (скорости вращения электродвигателя) по каналу регулирования не более 2%; - время регулирования- не более 1 сек.; - колебательность- 2-3 периода; - перерегулирование- до 20%. В лабораторной работе должны быть выполнены следующие задания: - определение рабочей точки объекта управления, согласно варианту; - определение передаточного коэффициента k Д в передаточной функции объекта управления; - линеаризация статической характеристики широтно-импульсного модулятора в окрестности рабочей точки, определение передаточного коэффициента ШИМ; - определение выходного напряжения тахогенератора в рабочей точке; - разработка структурной и алгоритмической схем систем автоматического управления; - представление передаточной функции непрерывной части системы в дискретной z-форме, определение интервала дискретности времени; - определение области устойчивости, определение параметров дискретного ПИ-регулятора; - расчет переходного процесса в системе при скачкообразном задающем воздействии; - анализ проектируемой системы автоматического управления по параметрам переходного процесса; - оформить отчет и сделать выводы. Вариант задания определяется порядковым номером студента в журнале. В рабочей точке для N-ого варианта объект управления имеет следующие значения переменных: - момент на волу двигателя М=10 + 2N, (Hм); - угловая скорость вращения вала 250 5 N , (с-1), 2. Методические указания и пример выполнения варианта лабораторной работы. 2.1 Выполнение работы следует начинать с определения рабочей точки системы. Согласно технического задания двигатель в установившемся режиме должен создать на валу вращательный момент М=10+2*20=50 (Нм) при угловой скорости вращения вала 250 5 * 20 150 (с-1). Пользуясь нагрузочными характеристиками (Рис. 1.1) найдём необходимое для этого напряжение, подаваемое на цепь якоря. Эту задачу можно решить графическим или аналитическим методами. Графический способ даёт значение напряжения U=70В, это видно из рисунка 2.1 Рис. 2.1. Таким образом, при подаче на цепь якоря двигателя напряжения 70Ввходной сигнал, при нагрузке 50Нм в установившемся режиме, угловая скорость вала двигателя 150с-1- выходной сигнал. Отсюда находим передаточный коэффициент k Д в передаточной функции двигателя с нагрузкой: W ( p) kД 1,5 p 1 . При p 0 kД 1,5 p 1 70 150 , k Д 150 2,14 . 70 Передаточная функция объекта управления принимает вид: W ( p) 2,14 . 1,5 p 1 Так, как, статическая характеристика ШИМ нелинейная, проведем линиарезацию в окрестности рабочей точки Uвых=70В для данного звена системы, переходя к новым координатам. При входных напряжениях 2В и 2,5В соответствующие выходные напряжения равны 63В и 73В. Уравнение прямой, проходящей через эти две точки Uвых=20Uвх+23. Отсюда U ВЫХ 20 U ВХ , где U ВЫХ - изменение выходного напряжения в окрестности рабочей точке ШИМ; U ВХ - изменение входного сигнала в окрестности рабочей точки. Коэффициент 20 – передаточный коэффициент (передаточное число) широтно-импульсного модулятора – регулирующего органы системы. В стационарном режиме для создания входного напряжения на двигателе 70В, на входе ШИМ должен бить U ВХ , значение которого найдем из уравнения 70 20 U ВХ 23 ; U ВХ 2,35B . Угловая скорость вращения вала электродвигателя 150 с-1 преобразовывается тахогенератором в выходное для него напряжение U=5,5*10-3*150=0,825 В. 2.2 Разработка структурной и алгоритмической схем САУ. Структурная схема системы автоматического управления представлена рисунке 2.2 Микроконтроллер Непрерывная часть системы Задатчик ЦАП ВУ Угловая скорость Двигатель и нагрузка ШИМ Тахогенератор АЦП Обратная связь Рис. 2.2 В состав проектируемой системы входят: - объект управления- двигатель постоянного тока с нагрузкой; - регулирующий орган- широтно-импульсный модулятор (ШИМ); - измерительный преобразователь скорости вращения вала двигателятахогенератор; - микроконтроллер, содержащий в составе: вычислительное устройство (ВУ), аналого-цифровой преобразователь (АЦП), цифро-аналоговый (ЦАП). Непрерывная часть системы состоит из объекта управления, ШИМ и ЦАП. Обозначим передаточную функцию, непрерывной части, Wнч(p)=W(p). В цепи обратной связи, тахогенератор преобразовывает сигнал на выходе объекта управления- частоту вращения вала в напряжении 0,825В, которое поступает на вход АЦП. С выхода АЦП сигнал, преобразованный в дискретную цифровую формулу, поступает в блок сравнения ВУ, где происходит его вычитание из цифрового сигнала задатчика (150) и формируется сигнал рассогласования. В данной цифровой системе автоматического управления обратная связь является отрицательной, с коэффициентом передачи (-1). Согласно техническому заданию, необходимо запрограммировать ВУ микроконтроллера на реализацию ПИ-закона регулирования; установить задающий сигнал – частоту вращения вала электродвигателя 150 с-1; задать тактовую частоту, определив дискретность интервала времени. Алгоритмическая структура системы автоматического управления будет иметь вид, представленный на рисунке 2.3. X(z) + D(z) W(Z) Y(z) Рис. 2.3 D(z) - дискретная передаточная функция ПИ-регулятора; W(z) - дискретная передаточная функция непрерывной части системы. 2.3. Представление передаточной функции непрерывной части системы в дискретной z-форме. Передаточная функция двигателя с нагрузкой: W1 ( p) 2,14 . 1,5 p 1 Постоянная времени данного объекта Т=1,5с. При подаче на вход напряжения 70В, вал двигателя достигает установившейся скорости вращения 150 с-1 за время 4 5T , т.е. за 6- 7,5 с. График переходного процесса, смоделированного в прикладном программном пакете VisSim для данного объекта без системы автоматического управления представлен на рисунке 2.4. Согласно техническому заданию в проектируемой замкнутой системе управления, время разгона должно быть не более 1 с. Интервал дискретности по времени t T0 должен быть хотя бы на порядок меньше времени разгона. Поэтому для дальнейших расчетов принимаем значение Тo = 0,1 с. Рис. 2.4 Получим передаточную функцию непрерывной части системы в дискретной форме при Тo = 0,1 с. Непрерывная часть состоит: из объекта управления – двигателя с нагрузкой; регулирующего органа – ШИМ; цифроаналогово преобразователя – ЦАП. В качестве ЦАП применим экстраполятор нулевого порядка, с передаточной функций: W0 ( p) 1 e pT0 ) . p Передаточная функция ШИМ имеет вид: W2 ( p) 20 . Передаточная функция всей непрерывной части системы имеет вид: W ( p) W2 ( p) W0 ( p) W1 ( p) После подстановки получим: 1 e pT0 2,14 1 (1 e pT0 ) . W ( p) 20 42,8 p 1,5 p 1 (1,5 p 1) p Множитель 1 представим в виде суммы двух простых дробей: (1,5 p 1) p 1 1 1,5 , (1,5 p 1) p p 1,5 p 1 тогда 1 1 1,5 1 1 e pT0 42,8 1 e pT0 . W ( p) 42,8 p 1,5 p 1 p p 0,667 Из таблицы (1.1.1) находим соответствующие представления выражений в дискретной z-форме: 1 z ; p z 1 1 z z , p 0,667 z e 0,667T0 z 0,93 0, 667T0 z e0,0667 0,930 ; значение z e 1 e 1 z . pT0 1 Сделав соответствующие подстановки получим передаточную функцию непрерывной части системы в z-форме: z z W ( z ) 42,8 1 z 1 . z 1 z 0 , 93 После алгебраических преобразований это выражение принимает окончательный вид: W ( z) 3 . z 0,93 2.4. Определение области устойчивости САУ. Определение параметров ПИ-регулятора. Дискретная передаточная функция замкнутой системы с единичной отрицательной обратной связью находится из выражения: П ( z) D( z ) W ( z ) , 1 D( z ) W ( z ) где D(z) – передаточная функция ПИ-регулятора, которая в дискретной zформе имеет вид: T 1 , D( z ) k1 1 0 1 TИ 1 z где k1, ТИ – параметры регулятора, Т0 – интервал дискретности времени. Определим область устойчивости САУ и выберем значения параметров регулятора k1 и ТИ из найденной области устойчивости. Прировняв знаменатель выражения характеристическое уравнение: к нулю, получим 1 D( z ) W ( z ) 0 . 0,1k1 . TИ Передаточная функция непрерывной части: В таком случае, 1 D( z ) W ( z ) 1 После П(z) k 0,1 0,1 1 1 k1 1 D( z ) k1 1 1 TИ 1 z 1 TИ 1 z k2 ( k k 2 ) z k1 k1 1 1 z 1 1 z При Т0 =0,1с.: где k 2 для алгебраических W ( z) 3 . z 0,93 (k1 k 2 ) z k1 3 0. z 1 z 0,93 преобразований характеристическое уравнение принимает вид: z 2 (3k1 3k 2 1,93) z (0,93 3k1 ) 0 . Для определения искомых параметров настроек k1 и k2, при которых система устойчива, воспользуемся методом замены переменных. Подставляя в полученное уравнение z 1 , получим: 1 3k 2 2 (0,14 6k1 ) (3,86 6k1 3k 2 ) 0 . Условием вещественной устойчивости части корней системы полученного является уравнения. отрицательность Для этого в соответствии с алгебраическим критерием устойчивости Раусса, должны выполняться неравенства: 3k 2 0 . 0,14 6k1 0 3,86 6k 3k 0 1 2 Первые два неравенства очевидны. Из третьего получаем: k 2 2k1 1,287 . На рисунке 2.5 изображена область устойчивости по параметрам k1 и k2, цифровой системы автоматического управления двигателем постоянного тока с нагрузкой. Рис. 2.5. Из графика видно, что значения коэффициента усиления k1 ПИрегулятора ограничено, k1 < 0,64. Возьмем значение k1 = 0,3(k1 = 0,3 < 6,4) из области устойчивости настроек. При значении k2 = 0,3 , из выражения k2 0,1k1 TИ получим значение TИ = 0,1 с, что равно интервалу дискретности по времени. При TИ = 0,5с., значение k 2 0,1 0,3 0,6 , что принадлежит области 0,5 устойчивости. Принимаем значения параметров ПИ-регулятора: k1 =k2 = 0,3 и TИ = 0,1с., выражение для передаточной функции цифрового ПИ-регулятора с полученными параметрами из области устойчивости настроек, принимает вид: 1 0,36 z 0,3 0,1 D( z ) 0,31 1 z 1 0,5 1 z 2.5. Построение алгоритмической цифровой модели системы управления и анализ переходного процесса. По полученным передаточным функциям в дискретной z- форме ПИрегулятора и объекта управления с блоком силовой электроники, используя контур обратной связи строим модель системы управления (рис. 2.6.) По графику переходного процесса определяем: - точность регулирования 100% 152 150 100 1,3% , 150 макс 165 150 100% 100% 9,0% 150 - перерегулирование - время регулирования- не более 1 сек. 150.36 PI 150 * + - 1 0.36z-0.3 1 z-1 Plot 3 200 z-0.93 * 175 150 125 100 75 50 25 0 0 .25 .5 .75 1 1.25 Time (sec) 1.5 1.75 Рис. 2.6. Можно сделать вывод, что спроектированная цифровая система управления соответствует техническому заданию. Модуль является первым компонентом в планируемом комплексе информационно- методических модулей для дистанционного образования инженерных кадров. Внедрение модуля в образовательный процесс создаст возможность дистанционного изучения дисциплины и позволит повысить качество образования инженерных кадров. 2 Список литературы. 1. Грыжов В.К., Корольков В.Г. Применение виртуальных лабораторий в обучении техническим дисциплинам. Заочная научно- практическая конференция «Региональные особенности развития современного образования»- г. Смоленск: СГПУ, 5 апреля 2004 г. 2. Грыжов В.К., Корольков В.Г. Особенности методики оптимизации систем автоматического управления по интегральному критерию качества. Методический сборник. Работы преподавателей Филиала Московского государственного университета технологий и управления в г. Вязьме. Выпуск 1., Смоленск- Вязьма 2008 г. . 3. Корольков В.Г., Грыжов В.К. Модель времяимпульсного цифрового вольтметра для измерений в реальном режиме времени постоянных и изменяющихся напряжений в среде VisSim печатная Научные труды XIV Международной научно-методической конференции: «Стратегия развития образования: эффективность, инновации, качество», Вып. 12. Москва, МГУТУ, 2008. Корольков В.Г. 4. Ротач В.Я. Теория Автоматического управления. Учебник для вузов, 2-е издание. – М.: «МЭИ» 2004 г. 5. Олссон Г., Пиани Д. Цифровые системы автоматизации и управления. – Санкт-Петербург: «Невский диалект» 2001 г.