Preobrazovanie_grafikov
реклама

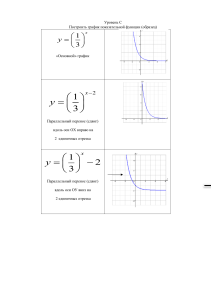
Сводная таблица преобразований графиков Пусть на координатной плоскости задан график некоторой функции y = f(x). Тогда: 1. y = f(x-a), a>0 Параллельный перенос вдоль оси х вправо на а единиц 2. y = f(x+a), a>0 Параллельный перенос вдоль оси х влево на а единиц 3. y = f(x)+а, a>0 Параллельный перенос вдоль оси y вверх на а единиц 4. y = f(x)-а, a>0 Параллельный перенос вдоль оси y вниз на а единиц 5. y = f(x*a), a>1 Сжатие вдоль оси х в а раз 6. y = f(x/a), a>1 Растяжение вдоль оси х в а раз 7. y= af(x), a>1 Растяжение вдоль оси у в а раз 8. y= f(x)/a, a>1 Сжатие вдоль оси у в а раз 9. y = - f(x) Зеркальное отражение относительно оси х 10. y = f(-x) Зеркальное отражение относительно оси у 11. y = - f(-x) Центральная симметрия относительно начала координат 12. x = f(y) Зеркальное отражение относительно прямой у = х. (Если функция y = f(x) монотонна на всей области определения, то данное преобразование задает построение графика функции, обратной к f(x)) 13. y f(x) - Часть графика, лежащую выше оси ОХ, оставить без изменений,, а часть графика, лежащую ниже оси Ох, отразить зеркально в верхнюю полуплоскость. 14. y f x - часть графика, лежащую левее оси Оу, стереть, а часть графика, лежащую правее оси Оу, оставить без изменений и отразить зеркально относительно Оу. 15. y f(х)-часть графика, лежащую ниже оси Ох, стереть, а часть графика, лежащую выше оси Ох, оставить без изменений и отразить зеркально относительно Ох. Линейная функция, прямая на плоскости. 1. Расстояние между точками x1 ; y1 и x2 ; y2 равно x2 x1 2 y2 y1 2 2. Уравнения прямой : а) в явной форме: y kx b , где k – угловой коэффициент, который равен тангенсу угла наклона прямой к положительному направлению оси х. б) в неявной форме: ax + by = c. Здесь k a / b . x y в) в отрезках: 1. Здесь p и q – отрезки, которые прямая p q отсекает от осей координат г) проходящей через данную точку x1 ; y1 : y y1 k ( x x1 ) д) проходящей через две заданные точки x1 ; y1 и x2 ; y2 : y y1 y 2 y1 ( x x1 ) x2 x1 3. Расстояние от точки x0 ; y 0 до прямой ax + by = c равно ax0 by0 c a 2 b2 4. Расстояние между двумя параллельными прямыми ax + by = c и ax by d равно c d 2 a b2 5. Две прямые y k1 x b1 и y k 2 x b2 параллельны, если k1 k 2 , перпендикулярны если k1 k 2 1 6. Две прямые ax by c и px qy r параллельны, если aq-bp=0, перпендикулярны если ap+bq=0. 7. Тангенс угла между двумя неперпендикулярными прямыми k k y k1 x b1 и y k 2 x b2 вычисляется по формуле tg 2 1 1 k1 k 2