10 класс
реклама

10 класс
5. Решение:
P(x)=(x-2)Q1(x)+5 и P(2)=5
P(x)=(x-3)Q2(x)=7и P(3)=7
пусть
P(x)=(x^2-5x+6)Q(x)+ax+b
тогда
P(x)=(x-2)(x-3)Q(x)+ax+b
P(2)=(2-2)(2-3)*Q(x)+a*2+b=5
P(3)=(3-2)(3-3)*Q(x)+a*(3)+b=7
получаем систему уравнений
a*2+b=5,
a*3+b=7.
и решаем ее
a=2.
b=7-a*3.
получаем
a=2,
b=1.
Ответ: остаток 2x+1.
f := 2*x^4+2*y^4-4*x*y-1;
В декартовой системе координат данная кривая описывается двумя линиями:
7. 2 метод решения
Решить уравнение 2 x 4 2 y 4 4 xy 1
(x + 2)4 + (x + 2)2 – a(a – 1) = 0 (x + 2)2 = –a или (x + 2)2 = a – 1; при 0 < a < 1 решений нет; при а = 0 или а = 1 одно
решение; при а < 0 или а > 1 два решения.
Преобразуем уравнение к виду 2(x² - y²)² + (2xy - 1)² = 0. Сумма квадратов нескольких чисел может равняться нулю
только, когда каждый квадрат равен нулю. Остаётся решить систему:
𝑥² − 𝑦² = 0
{
2𝑥𝑦 − 1 = 0
Ответ:(
1
→𝑦=
;
1
√2 √
1
𝑦=√
2∗𝑥
) ; (−
2
1
√2
;−
1
√2
).
1
4𝑥 2
=
1
2𝑥
8
Дан многочлен x(x + 1)(x + 2)(x + 3). Найти его наименьшее значение.
Решение
x(x + 3)(x + 1)(x + 2) = (x2 + 3x)(x2 + 3x + 2). Обозначим x2 + 3x через z. Тогда (x2 + 3x)(x2 + 3x + 2) = z(z + 2) = (z + 1)2 –
1. Наименьшее значение –1 этой функции достигается при z = –1. Уравнение x2 + 3x + 1 = 0 имеет решения (дискриминант
больше нуля), следовательно, такое x, при котором наша функция достигает значения –1, существует.
Ответ:–1.
9.
Решение: Пусть x – первоначальная сумма. Через год будет – x +
Составим уравнение :
x+
1
x+
12
x+
1
12
x+
12
12+12+1
144
1
(x +
1
12
1
x) – x = 16900,
12
x+
1
144
𝑥 = 16900,
25
144
x = 16900,
X = 16900/
25
144
,
x – x = 16900,
1
x , а в следующий год будет x +
12
1
x+
12
1
12
(x +
1
x).
12
X = 16900 *
X = 97344.
144
25
,
Ответ: первоначальная сумма – 97344.
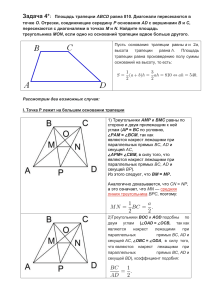
10
B
Треугольники BOC и COD имеют общую высоту,
если принять за их основания отрезки BO и OD.
1
S
BO
Тогда BOC
k . Следовательно, SCOD S BOC .
k
SCOD OD
C
O
Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда
A
S AOB
D
S BOC CO
k и
S AOB OA
1
S BOC .
k
Из этих двух предложений следует, что SCOD S AOB .
Так как SCOD S AOB . Отсюда S ABCD S1 S2 2SCOD , из подобия треугольников BОC и AOD следует, что
S1
SCOD
BO
OD
S1
SCOD S1 S2 . Тогда S ABCD S1 S 2 2 S1 S 2
S2
2
S1 S 2 .
BO
OD
S1
.Следовательно,
S2