1. Общая постановка
реклама

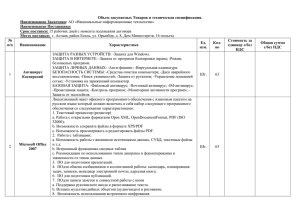
1. Общая постановка задачи математического программирования. Задача формулируется таким образом: среди элементов , образующих множество X, найти такой элемент, который доставляет минимальное значение заданной функции . Для корректной постановки задачи требуется задать допустимое множество X (с помощью ограничений), целевую функцию , а также критерий поиска (минимум/максимум). Тогда решить задачу означает либо найти такое , при котором . В случае, если множество X является множеством всех возможных значений, то это задача безусловной оптимизации, в обратном случае – условной. Порядок поиска решений: 1. Поиск всех точек стационарности 2. Выбор тех, что принадлежат области допустимых решений 3. Проверка граничных точек. Сложность решения зависит от размерности. Например, может потребоваться проверить условие на границе, заданной линией, т.е. в бесконечном количестве точек. Задача на условный экстремум включает ограничения: - это ограничение типа равенство. Этап поиска условий экстремума – обычно аналитический, а вычисления оптимальных решений – инженерный. 2. Метод неопределенных множителей Лагранжа при поиске максимальных значений функций. Требуется найти экстремум функции , которая зависит от n переменных и эти переменные связаны m соотношениями , причем m<n, иначе решение было бы тривиальным. Для решения методом неопределенных множителей Лагранжа составим функцию . Составим систему из n+m уравнений, приравняв нулю частные производные функции Лагранжа по и . Если полученная система имеет решения относительно своих параметров, то точка x может быть решением исходной задачи, то есть условным экстремумов. На картинке изображены линии уровня при условии . Данное уравнение задает кривую S. Пример. Найти экстремум функции при ограничении . Составляем функцию Лагранжа , откуда Правда, можно было решить проще: выразить из ограничений одну переменную через другую, подставить в функцию и найти экстремум функции одной переменной: например . 3. Линейный функционал. Функционалом называют отображение, аргументов которого является функция вещественной переменной, а результатом – вещественное число. Функционал обозначим . Функционал является линейным, если он удовлетворяет принципу суперпозиции: . Другое определение: функционалами называются величины, значение которых определяются выбором одной или нескольких функций. Пример: длина дуги пространственной кривой, соединяющей заданные точки. Исторические предпосылки введения функционалов: 1. Геодезические линии. Найти линию минимальной длины между двумя точками при некотором условии. 2. Изометрическая задача. Найти замкнутую линию заданной длины, ограничивающей максимальную площадь. Условие на постоянство длины кривой называется изопараметрическим. 3. Задача о брахистохроне. На плоскости, требуется попасть из одной точки в другую без начальной скорости и только за счет силы тяжести за минимальное время. Функционал непрерывен, если малому изменению соответствует малое изменение функционала. Функции можно считать близкими, если мал модуль их разности при любом x из области определений. Но так как часто функционал зависит еще от производных, желательно считать близкими функции, также близкие по своим производным (1-й порядок близости). 4. Понятие вариации функционала. Вариация функционала позволяет определить экстремум функционала. Вариация функционала обозначается как и выглядит как приращение к «точке» (то есть функции, так как у нас исходная часть – не функция, а функционал) . Такое приращение называется вариацией аргумента и оно должно принадлежать тому же выбранному линейному нормированному пространству. Необходимое условие экстремума заключается в равенстве нулю вариации функционала. Проще говоря – как бы мы не толкали наши функцию, она в любом случае будет иметь один и тот же знак, то есть будет сидеть в экстремуме. 5. Вычисление вариации функционала. Для вычисления вариации функционала запишем: где – линейный функционал относительно второго аргумента, – бесконечно малая величина высокого порядка. Учитывая свойство линейности функционала L, можно записать При переходе при получаем . Дифференциальное уравнение Эйлера в данном случае является линейным, имеющим второй порядок: . Решая его и подставляя граничные значения , можно получить оптимальную траекторию движения, а затем уже и выразить оптимальное управление. 9. Понятие близости кривых. См. 3. . 6. Постановка задачи Эйлера. Нужно найти функцию, которая соответствует критерию оптимальности. 10. Уравнение Эйлера-Пуассона. Рассматривается функционал вида , т.е. зависящий от старших производных.. На функцию наложены граничные условия: и такие же для . Используя рассуждения из билета 6, можно прийти к выводу: Рассматривается функционал вида . Требуется провести через две заданные точки с координатами и такую кривую , которая доставила бы экстремум заданному функционалу. Вычислим вариацию рассматриваемого функционала: 11. Пример использования уравнения Эйлера-Пуассона в теории оптимального управления. Пусть имеется динамическая система, описываемая уравнением . Требуется перевести систему из состояния в состояние за время так, чтобы функционал принимал бы минимальное значение. Уравнение Эйлера-Пуассона примет вид где – вариация с границами . Проинтегрировав по частям второе слагаемое, получим: , общее решение которого выглядит как . Эти коэффициенты находятся с использованием заданных значений функции и ее производных при нулевом и конечном времени, а затем из этого выражается оптимальное управление. 12. Вариационные задачи с подвижными границами. Пример в теории управления. Рассмотрим задачу об экстремуме функционала Тогда получим условие экстремума: Основная лемма вариационного исчисления позволяет записать условие экстремума в виде дифференциального уравнение для искомой кривой: . Кстати, может быть не очевидно, но . А уравнение это – уравнение Эйлера. 7. Уравнение Эйлера. В предыдущем уравнении все расписано норм так. 8. Пример использования уравнения Эйлера для поиска оптимального управления. Пусть имеется динамический объект, описываемый дифференциальным уравнением . Требуется перевести за время T объект из состояния в состояние так, чтобы функционал имел минимальное значение. Решаем: представим функционал в виде, для которого можно сформулировать задачу Эйлера: Функция – дважды дифференцируемая. На допустимые функции нет ограничений в виде граничных условий. Подсчет вариации дает . Приравняв ее к нулю, чтобы найти экстремаль, получим выражение 1: . По основной лемме вариационного исчисления получаем выражение 2: . В то же время, если посчитать выражение 1 по частям: который Интеграл в правой части равен 0 из выражения 2. Значит Так как вариации в точках a и b могут меняться произвольно, можно записать: Получили уравнение Эйлера с естественными краевыми условиями. 13. Вариационные задачи на условный экстремум. Имеется функционал вида Каждая из функций проходит через две заданные для нее точки, на функции наложены ограничения вида . Требуется найти экстремум функционала. Для этого вводим множители Лагранжа в функционал, образуется новый функционал: Находится экстремум этого функционала, оставляются функции , при которых достигается экстремум функционала. Условный экстремум исходного функционала вычисляется с использованием выделенных функций . 14. Множители Лагранжа в вариационном исчислении. Все есть в предыдущем билете, его перепиши лучше, блин надо растянуть все что я тут напишу еще на строчку, чтобы уместился следующий билет. 15. Пример использования множителей Лагранжа для поиска управлений. Пусть имеется динамический объект, описываемый дифференциальным уравнением . Требуется перевести его из состояния в состояние за время так, чтобы функционал имел минимальное значение. Образуем с помощью множителей Лагранжа новый функционал: . Тогда система уравнений Эйлера имеет вид: Исключая и получим дифференциальное уравнение для функции вида . Отсюда находим x и определяем оптимальное управление. требуется минимизировать . Задача оптимального управления заключается в нахождении функции состояния и управления для времени , которые минимизируют функционал. Есть три метода решения этой задачи: вариационным исчислением, принципом максимума Понтрягина, а также методом динамического программирования. 18. Линеаризация дифференциальных уравнений и ее использование при получении принципа максимума. Имеется дифференциальное уравнение , граничные условия . Требуется перевести за время T систему из одного состояния в другое так, чтобы функционал принял наименьшее/наибольшее значение при соблюдении ограничений . Введем для упрощения переменную такую, что и . Определяем понятие игольчатой вариации как узкий прямоугольный импульс (длительностью ε) с малой ненулевой площадью. Управляющему воздействию в момент времени И ТУТ МНЕ НАДОЕЛО 19. Принцип максимума. 20. Теорема о числе переключений. 21. Определение моментов переключения. 22. Принцип оптимальности. 23. Дискретная программирования. форма динамического 24. Учет ограничений программирования. в динамического методе 25. Постановка задачи линейного программирования. Задача допускает строгое алгоритмическое решение и определяется таким образом: в многомерном пространстве определяется область допустимых решений с помощью линейных ограничений типа равенств и неравенств: 16. Понятие переменных состояния. Короче блять хуйня. 17. Постановка задачи оптимального управления. Имеются уравнения состояния: или дифференциальные уравнения граничные условия где – известные числа , и функционал, Допустимое решение – это вектор , удовлетворяющий заданными выше ограничениями. Предполагается, что все составляющие вектора неотрицательны. Требуется найти такое допустимое решение, при котором линейная форма с известными численные коэффициентами принимает наибольшее (или наименьшее) значение. 26. Определение моментов переключения. Для определения экстремальных точек сперва определим выпуклое множество. Множество M будет выпуклым, если две любые точки A,B, принадлежащих множеству M, определяют отрезок прямой, целиком принадлежащий множеству M. Для выпуклого множества – круга экстремальными точками являются все точки на окружности, для выпуклого множество – многоугольника экстремальными точками являются все углы. Таким образом, чтобы точка была экстремальной, требуется, чтобы она лежала на отрезке, стягивающемся в точку, математически: . Теорема: Точка x является экстремальной тогда и только тогда, когда перестановка столбцом матрицы А может быть представлена в блочном виде так, что , где – невырожденная квадратная матрица порядка m, и . Например, имеется система уравнений этой . Для системы . положим . Фактически тогда это решение в случае, если . Так как в решении присутствуют отрицательные значения, то оно не является экстремальным (и вообще, не принадлежит множеству значений данной системы уравнений). После перестановки в уравнении переменных местами можно получить экстремальные решения. Сам займись. Кстати, число экстремальных точек не превышает величины , то есть возможного количество перестановок столбцом матрицы A. А еще у всякого непустого множества есть хотя бы одна экстремальная точка. И, кстати, линейная форма достигает наименьшего/наибольшего значения именно в экстремальной точке. 27. Симплексный метод. Выберем первую точку, значение линейной формы в ней будет . Можно ли найти точку со значением линейной формы меньше? Перепишем ограничения в виде Сперва , , Можно определить оптимальное решение перебором всех экстремальных точек, подставляя в них решение, но это может быть громоздко для большого количества точек. Поэтому есть более удобный способ – симплексный метод. Его суть заключается в нахождении хотя бы одной экстремальной точки, а затем передвижения от нее к другим точкам, пока такое движение будет возможно. Исчезновение этой возможности означает, что точка – оптимальна (минимальна/максимальна). Для начала путем теоремы о экстремальных точках (билет предыдущий) находим одну из точек. Например, требуется найти наименьшее значение линейной формы при ограничениях . Найдем экстремальные точки: (сам посчитаешь) Переменные, имеющие значения в исходной экстремальной точки, называются базисными, а нулевые переменные – свободными. Решая система относительно базисных переменных, получим: Подставляя в линейную форму: . Теперь попробуем уменьшить значение линейной формы, увеличивая значение величины, входящей в уравнение с отрицательным знаком, то есть . Увеличивая значение, до тех пор, пока одна из базисных переменных не станет равной нулю (потому что они должны быть неотрицательны), получим другую экстремальную точку, в нашем случае . В этой точке значение линейной формы будет , а в ее уравнении все коэффициенты входят с положительными коэффициентами, поэтому уменьшать и дальше форму мы не можем. Таким образом, решение закончено. Замечание: если бы на окончательном шаге одна из переменных входила с нулевым коэффициентом, это бы означало, что существует множество точек, в которых значение линейной формы минимально. 28. Геометрическая интерпретация симплексного метода. Смотри, короче, предыдущий билет, и особенно картинку. Линейная форма – плоскость, пересекающая этот многоугольник на рисунке. Типа. И википедию почитай, там ясней. 29. Учет ограничений типа неравенств в линейном программировании. В постановке задачи линейного программирования присутствуют ограничения в виде неравенств, которые можно перевести в ограничения типа равенств, используя дополнительные переменные. Каждому ограничению соответствует одна дополнительная переменная. Например, задано ограничение . Введем вспомогательную переменную , тогда неравенство будет выглядеть как . Теперь у задачи больше ограничений, но в целом все осталось постарому!