Площади многоугольников на координатной сетке
реклама
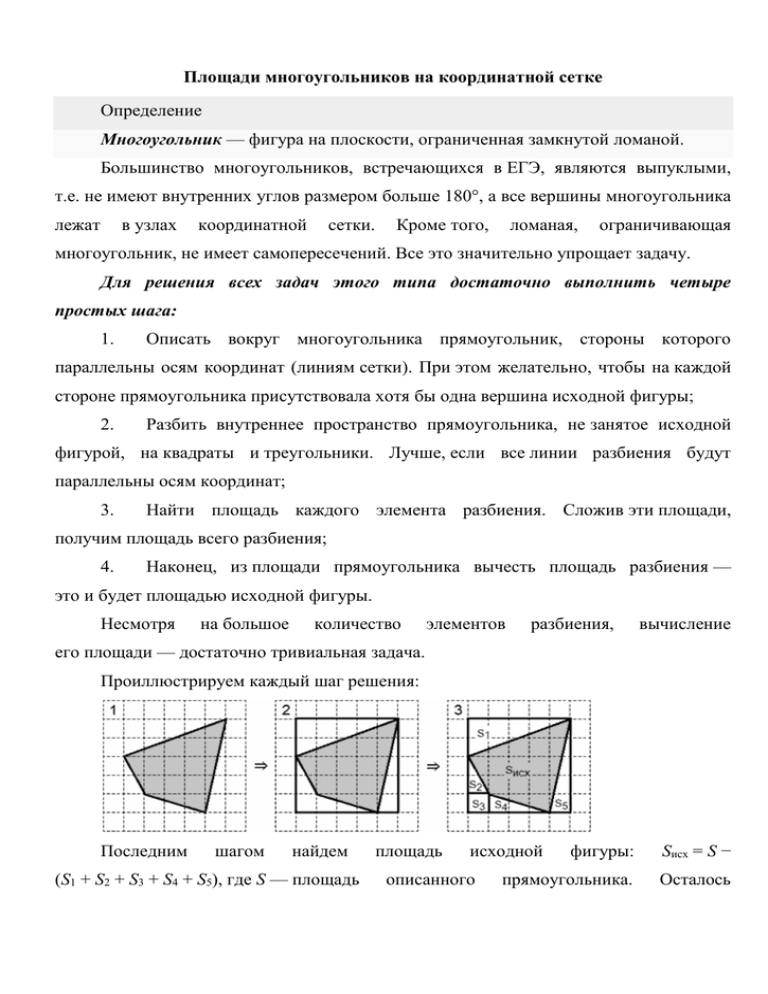
Площади многоугольников на координатной сетке Определение Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной. Большинство многоугольников, встречающихся в ЕГЭ, являются выпуклыми, т.е. не имеют внутренних углов размером больше 180°, а все вершины многоугольника лежат в узлах координатной сетки. Кроме того, ломаная, ограничивающая многоугольник, не имеет самопересечений. Все это значительно упрощает задачу. Для решения всех задач этого типа достаточно выполнить четыре простых шага: 1. Описать вокруг многоугольника прямоугольник, стороны которого параллельны осям координат (линиям сетки). При этом желательно, чтобы на каждой стороне прямоугольника присутствовала хотя бы одна вершина исходной фигуры; 2. Разбить внутреннее пространство прямоугольника, не занятое исходной фигурой, на квадраты и треугольники. Лучше, если все линии разбиения будут параллельны осям координат; 3. Найти площадь каждого элемента разбиения. Сложив эти площади, получим площадь всего разбиения; 4. Наконец, из площади прямоугольника вычесть площадь разбиения — это и будет площадью исходной фигуры. Несмотря на большое количество элементов разбиения, вычисление его площади — достаточно тривиальная задача. Проиллюстрируем каждый шаг решения: Последним шагом найдем (S1 + S2 + S3 + S4 + S5), где S — площадь площадь исходной описанного фигуры: Sисх = S − прямоугольника. Осталось вычислить площадь большого прямоугольника и элементов разбиения. Эти несложные расчеты предлагается выполнить читателю в качестве упражнения. Задача 1 Найти площадь треугольника ABC, изображенного на рисунке: Решение Обозначение треугольника можно опустить, поскольку оно нам не потребуется. Приведем первые три шага: Итак, Sисх = S − (S1 + S2 + S3), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения: S1 = ½ · 1 · 5 = 2,5; S2 = ½ · 3 · 4 = 6; S3 = ½ · 1 · 4 = 2; S = 5 · 4 = 20. Наконец, найдем площадь треугольника: Sисх = 20 − (2,5 + 6 + 2) = 9,5. Ответ: 9,5 Задача 2 Найти площадь треугольника ABC, изображенного на рисунке: Решение Снова выполняем первые три шага. Заметим, что угол ABC — тупой, поэтому в разбиении присутствует квадрат. Имеем: Очевидно, Sисх = S − (S1 + S2 + S3 + S4), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения: S1 = ½ · 5 · 5 = 12,5; S2 = ½ · 4 · 1 = 2; S3 = ½ · 1 · 4 = 2; S4 = 1 · 1 = 1;S = 5 · 5 = 25. Площадь треугольника: Sисх = 25 − (12,5 + 2 + 2 + 1) = 7,5. Ответ: 7,5










