Задание по геометрии для 7 В класса

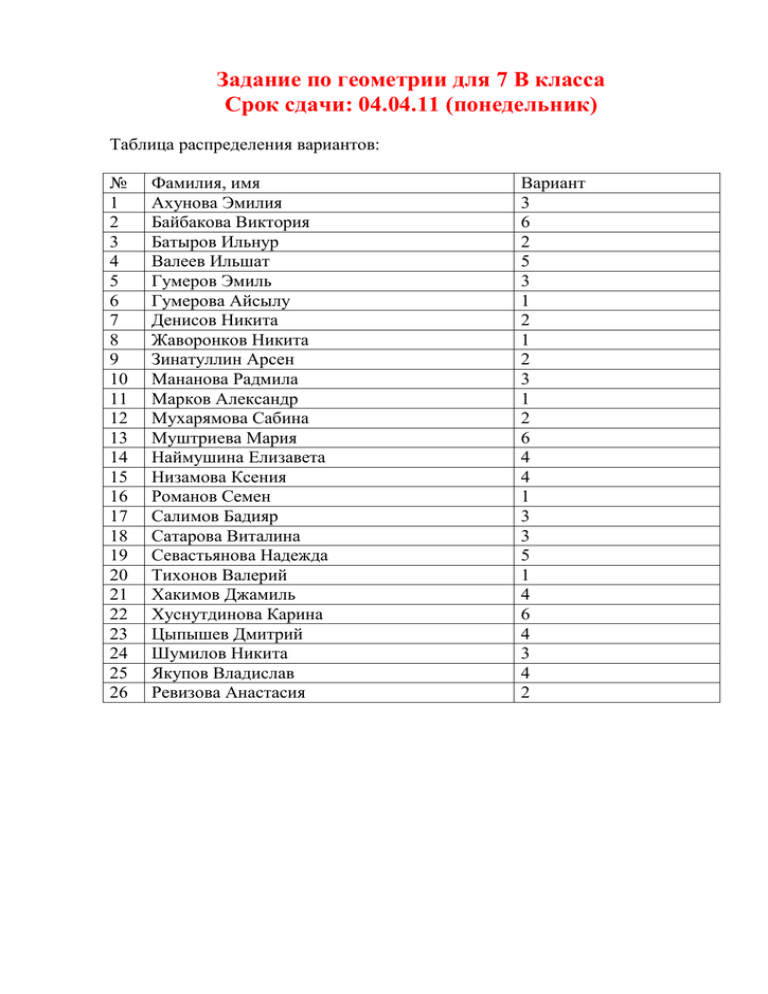
Задание по геометрии для 7 В класса
Срок сдачи: 04.04.11 (понедельник)
Таблица распределения вариантов:
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Фамилия, имя
Ахунова Эмилия
Байбакова Виктория
Батыров Ильнур
Валеев Ильшат
Гумеров Эмиль
Гумерова Айсылу
Денисов Никита
Жаворонков Никита
Зинатуллин Арсен
Мананова Радмила
Марков Александр
Мухарямова Сабина
Муштриева Мария
Наймушина Елизавета
Низамова Ксения
Романов Семен
Салимов Бадияр
Сатарова Виталина
Севастьянова Надежда
Тихонов Валерий
Хакимов Джамиль
Хуснутдинова Карина
Цыпышев Дмитрий
Шумилов Никита
Якупов Владислав
Ревизова Анастасия
Вариант
3
6
2
5
3
1
2
1
2
3
1
2
6
4
4
1
3
3
5
1
4
6
4
3
4
2
Вариант 1.
1) На сторонах АВ и АС треугольника АВС отмечены точки D и Е,
причем точка D является серединой отрезка АВ, АЕ = 12 см, DЕ = 1 см.
Может ли длина отрезка АВ быть равной 27 см?
2) В треугольнике АВС, С = 60, В = 90. Высота ВВ1 равна 2 см.
Найдите ВА.
3) Внутри неразвернутого угла А взята точка D. Из этой точки проведены
перпендикуляры DB и DC к сторонам угла. ADB = ADC. Докажите,
что луч AD – биссектриса угла А.
Вариант 2.
1) На продолжении стороны АВ треугольника АВ за вершину В отмечена
точка D. АС = 18 см, ВС = 5 см. Может ли отрезок AD быть равным 12
см?
2) В треугольнике АВС, С = 90, СС1 – высота, СС1 = 5 см. ВС = 110 см.
Найдите САВ.
3) Два прямоугольных треугольника АВС и АВЕ имеют общую
гипотенузу АВ и лежат по разные стороны от нее. Известно, что АЕ =
ВС. Докажите, что САВ = ЕВА.
Вариант 3.
1) Треугольники АВD и BCD расположены по разные стороны от прямой
BD. ABD = BDC, ADB = DBC. Докажите, что BD + BC > AB.
2) В треугольнике АВС, С = 90, внешний угол при вершине В равен
150. АА1 – биссектриса, АА1 = 20 см. Найдите А1С.
3) Треугольники АВС и А1В1С1 равны, причем ВС = В1С1, ВА = В1А1.
Докажите, что высоты ВН и В1Н1 треугольников равны.
Вариант 4.
1) Треугольники АВЕ и ВСЕ расположены по разные стороны от прямой
ВЕ, АЕВ = ВЕС, АВЕ = ЕВС. Докажите, что ВЕ < АВ + ВС.
2) В треугольнике АВС, В = 90, СС1 – биссектриса, СС1 = 16 см,
ВС1 = 8 см. Найдите внешний угол при вершине А.
3) Треугольники АВС и А1В1С1 равны, причем высота ВН треугольника
АВС равна высоте В1Н1 треугольника А1В1С1, С = С1. Докажите,
что А = А1.
Вариант 5.
1) В треугольнике АВС А = 40, В = 70. Из вершины С вне
треугольника проведен луч СК так, что угол ВСК равен 10959’. Может
ли выполняться равенство АК = АС + СК?
2) В треугольнике АВС, С = 90, СР – высота треугольника, ВС = 2ВР.
Докажите, что АР = 3РВ.
3) Две биссектрисы треугольника пересекаются в точке О. Докажите, что
третья биссектриса проходит через точку О.
Вариант 6.
1) В треугольнике АВС А = 35, В = 71. На продолжении стороны АС
за вершину С взята точка К. Из вершины С проведен луч СЕ так, что
точки Е и В лежат по разные стороны от прямой АК и ЕСК = 741’.
Может ли выполняться равенство ВЕ + СЕ = ВС.
2) В треугольнике АВС, В = 90, ВН – высота, АВ = 2ВН. Докажите, что
3АС = 4АН.
3) Докажите, что биссектриса угла А треугольника АВС проходит через
точку пересечения прямых, содержащих биссектрисы внешних углов
при вершинах В и С.