Задачи межвузовской олимпиады по физике 2012

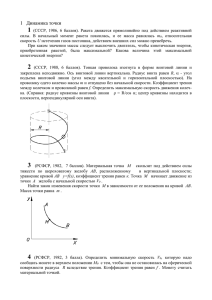
ЗАДАЧИ МЕЖВУЗОВСКОЙ ОЛИМПИАДЫ ПО ФИЗИКЕ 2012
(19 апреля 2012 года, СПбГЭТУ «ЛЭТИ»)
1. Мышонок стреляет из рогатки в кота, сидящего на ветке дерева. Через t = 1 с
камень попадает в ветку прямо у лап кота. На каком расстоянии s от мышонка находится
кот, если известно, что векторы v0 и v (t ) взаимно перпендикулярны.
2. Цилиндрическое тело радиуса R лежит на гладкой поверхности у гладкой стенки,
касаясь ее. Центр тяжести тела смещен от оси на расстояние, равное R/2. В начальный
момент времени тело лежит таким образом, что вектор от оси цилиндра к центру тяжести
направлен вертикально вверх. На какой угол повернется тело, прежде чем оторвется от
стенки?
3. На цилиндрическом карнизе для портьер свободно надето тонкое
кольцо. В нижней точке кольца находится улитка (см. рис.). Массы
улитки и кольца одинаковы. Улитка начинает медленно двигаться вверх
по кольцу. При каком минимальном значении коэффициента трения кольца о
карниз улитка сумеет добраться до верхней точки кольца?
4. Двухатомный идеальный газ расширяется в процессе с линейной
зависимостью его давления от объема. В результате этого процесса к газу было подведено
количество теплоты в 6 раз меньшее его внутренней энергии в начальном состоянии. Во
сколько раз увеличился объем газа, если в конечном состоянии величина его внутренней
энергии оказалась равной первоначальному значению? Под внутренней энергией газа
понимается сумма кинетических энергий всех молекул.
5. По диэлектрическому полукольцу массой m с центром
кривизны О равномерно распределен заряд Q>0. Полукольцо
способно без трения вращаться вокруг вертикальной оси,
проходящей через точку О. В точке О закреплен диполь с дипольным
моментом p. Ось диполя совпадает с осью симметрии полукольца
(прямая ОА). Полукольцо смещают из исходного положения так, что точка А
перемещается в точку А1. Длина дуги АА1 равна 0,1R (R – радиус полукольца). Какую
наибольшую скорость приобретет полукольцо при дальнейшем движении?
6. Имеется N идеально проводящих тел в вакууме с зарядами q1, q2 , qN и
потенциалами 1, 2, …., N. Какое количество тепла будет выделяться ежесекундно, если
пространство между этими телами заполнить однородной жидкостью с удельной
проводимостью σ и диэлектрической проницаемостью ε, а потенциалы тел поддерживать
при прежних значениях?
7. Экспериментальное исследование электрического поля Земли и соответствующие
расчеты показывают, что Земля в целом обладает отрицательным зарядом, среднее
значение которого оценивается в 5∙10-5 Кл. Вблизи поверхности Земли напряженность
электрического поля составляет в среднем E = 130 В/м. Определите электрический
дипольный момент металлического шара радиуса R = 0,85 м, находящегося вблизи
поверхности Земли.
8. По двум параллельным металлическим направляющим, наклоненным под углом α к
горизонту и расположенным на расстоянии b друг от друга, может скользить без трения
металлическая перемычка массы m. Направляющие замкнуты снизу на незаряженный
конденсатор емкости C, и вся конструкция находится в магнитном поле, индукция
которого B направлена вертикально. В начальный момент перемычку удерживают на
расстоянии l от основания «горки». За какое время перемычка достигнет основания
«горки», после того, как ее отпустят? Какую скорость она будет иметь у основания?
Сопротивлением проводников пренебречь.
9. На плоскую поверхность раздела вакуум – стекло из вакуума падает
перпендикулярно к поверхности световой пучок интенсивностью J = 1 кВт/м2. Найти
величину и направление силы, действующей на единицу площади поверхности раздела
сред, если показатель преломления стекла п = 1,5.
10. Найти теплоемкости Сv, Cp и уравнение адиабаты теплового излучения,
заключенного в сосуд с переменным объемом.
11. Рубиновый лазер излучает световой импульс с длиной волны  = 6935,9 Ао.
Длительность импульса  = 0,1 мс, энергия W = 0,3 Дж. Рассчитайте число фотонов N,
переносимых импульсом. Зная, что флуктуация числа фотонов в волне равна N1/2, получите
выражение для соответствующей флуктуации фазы  волны, связанной с N фотонами.
Дополнительные задачи:
1. Нагретый газ заставляют протекать через спиральную металлическую трубку
(змеевик), опущенную в воду калориметра. На одном конце змеевика поддерживают
постоянными давление P1 и температуру T1. На выходе змеевика поддерживают давление
P2 и измеряют температуру газа T2. По повышению температуры воды в калориметре
определяют количество тепла, отданное газом. Разделив полученное количество теплоты
на понижение температуры и на число молей прошедшего газа, находят его молярную
теплоемкость. Какую именно теплоемкость находят таким методом?
2. Мистер Бин решил не спеша прогуляться по краю большой круглой карусели
радиуса R, вращающейся с угловой скоростью ω, так что ωR << c. Сделав один полный
круг, он вернулся в исходную точку и сравнил показания своих наручных часов с
оставленными на краю карусели точно такими же часами. К своему удивлению он
обнаружил разницу в показаниях обоих часов. Решив, что он шел слишком быстро, он
повторил попытку, двигаясь теперь в 2 раза медленнее. Но вернувшись назад, обнаружил
опять ту же разницу в показаниях обоих часов. Вопрос: какую разницу в показаниях
обнаружил мистер Бин и, почему она не зависела от скорости его движения по карусели?
3. Две длинные проволоки расположены в плоскости ХОY. Одна из них – прямая –
совпадает с полуосью ОХ, а вторая имеет форму графика
функции y(x) = le  x 2 . Резистор R соединяет обе
проволоки в точках х = 0. По проволокам без трения
может скользить перемычка массой m, в начальный
момент расположенная вдоль оси ОY. Вся система
расположена в однородном магнитном поле с индукцией
В, направленной вдоль оси ОZ. Перемычке сообщают
скорость v0, направленную вдоль оси ОХ.
1). При каком минимальном значении vmin перемычка удалится на неограниченное
расстояние?
2). На какое расстояние переместится перемычка до остановки после сообщения ей
скорости v0=vmin/2?