предмет Математика

Тестовые задания по дисциплине Математика
1. Жарқын Айтбайқызы преподаёт математику в классе из 28 учеников. Она проверяет
контрольную работу одного школьника в среднем за 7 минут, а самостоятельную — за 2 минуты.
За неделю учительница провела одну контрольную работу и четыре самостоятельных. Сколько
времени Жарқын Айтбайқызы потратит на проверку? Ответ дайте в часах.
a) 7
b) 8
c) 6
d) 5
e) 9
2. В городе 125 тысяч жителей. 40% из них любят биатлон, из них 60% не смогли посмотреть
соревнования по телевизору. Сколько любителей биатлона увидели соревнования по телевизору?
Ответ дайте в тысячах человек.
a) 120
b) 20
c) 70
d) 35
e) 27
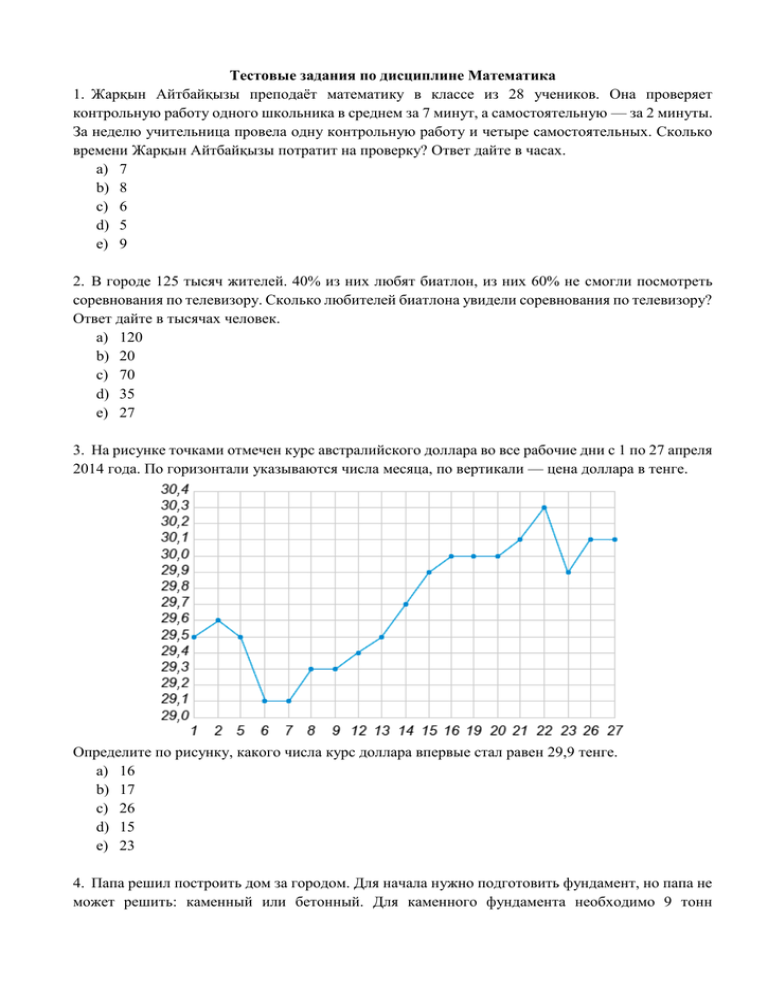
3. На рисунке точками отмечен курс австралийского доллара во все рабочие дни с 1 по 27 апреля
2014 года. По горизонтали указываются числа месяца, по вертикали — цена доллара в тенге.
Определите по рисунку, какого числа курс доллара впервые стал равен 29,9 тенге.
a) 16
b) 17
c) 26
d) 15
e) 23
4. Папа решил построить дом за городом. Для начала нужно подготовить фундамент, но папа не
может решить: каменный или бетонный. Для каменного фундамента необходимо 9 тонн
природного камня и 8 мешков цемента. Для бетонного фундамента необходимо 6 тонн щебня и
43 мешка цемента. Тонна камня стоит 1400 тенге, тонна щебеня стоит 750 тенге, а мешок цемента
стоит 230 тенге.
Сколько тенге будет стоить материал для фундамента, если папа выберет наиболее дешевый
вариант?
a) 15000
b) 14390
c) 13590
d) 14400
e) 14280
5. Найдите площадь треугольника, изображенного на рисунке.
a)
b)
c)
d)
e)
29
24
21
32
22
6. Жюри конкурса народной песни собирается прослушать в первые два дня по 15 человек, а в
третий день — оставшихся 20. С какой вероятностью артист Петров выступит во второй день,
если порядок выступлений участников определяется жребием?
a) 0,3
b) 0,5
c) 1
d) 1,4
e) 0,7
1 𝑥−1
7. Решите уравнение (6)
a)
b)
c)
d)
e)
−2
-1
1
2
3
= 216
8. Прямые, содержащие высоту CH и биссектрису AD треугольника ABC, пересекаются в точке
O, ∠BAD=63°. Найдите угол OAC. Ответ дайте в градусах.
a) 120
b) 117
c) 130
d) 119
e) 110
9. Прямая y=5x−7 касается графика функции y=6x2+bx−1 в точке с абсциссой меньше 0.
Найдите b.
a) 18
b) 20
c) 16
d) 10
e) 17
10. В кубе ABCDA1B1C1D1 найдите угол между прямыми BC1 и A1C1. Ответ дайте в градусах.
a) 70
b) 65
c) 60
d) 62
e) 72
11. Вычислите:−
a)
b)
c)
d)
e)
31𝑡𝑔176°
𝑡𝑔4°
.
15
20
21
31
25
12. Локатор
батискафа,
равномерно
погружающегося
вертикально
вниз,
испускает
𝑓−𝑓
ультразвуковые импульсы частотой 374 МГц. Батискаф спускается со скоростью 𝑣 = 𝑐 𝑓+𝑓0
0
метров в секунду, где c=1500 м/с — скорость звука в воде, f0 (МГц) — частота испускаемых
импульсов, f (МГц) — частота отраженного от дна сигнала, регистрируемая приемником.
Определите наибольшую возможную частоту отраженного сигнала f, если скорость погружения
батискафа не должна превышать 4 м/с.
a) 385
b) 376
c) 360
d) 500
e) 427
13. К резервуару объёмом 220 литров ведут две трубы, первая пропускает на 9 литров воды в
минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если
резервуар она заполняет на 9 минут дольше, чем вторая труба?
a) 11
b) 12
c) 14
d) 10
e) 13
14. На диаграмме показана средняя температура воздуха (в градусах Цельсия) в Алматы за
каждый месяц 2014 года.
Определите по диаграмме, сколько было месяцев, когда среднемесячная температура была
выше нуля.
a) 11
b) 7
c) 15
d) -11
e) -15
15. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет)
предлагает три тарифных плана.
Тарифный план
Абонентская плата
Плата за трафик
План "0"
Нет
2,5 тг. за 1 Мб
План "500"
550 тг. за 500 Мб трафика в месяц
2 тг. за 1 Мб сверх 500 Мб
План "800"
700 тг. за 800 Мб трафика в месяц 1,5 тг. за 1 Мб сверх 800 Мб
Пользователь предполагает, что его трафик составит 650 Мб в месяц, и исходя из этого выбирает
наиболее дешевый тарифный план. Сколько тенге заплатит пользователь за месяц, если его
трафик действительно будет равен 650 Мб?
a) 700
b) 750
c) 650
d) 800
e) 550
16. Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см
х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
a)
b)
c)
d)
e)
5
9
6
7
8
−𝑡
17. В ходе распада радиоактивного изотопа его масса уменьшается по закону 𝑚(𝑡) = 𝑚0 ⋅ 2 𝑇 ,
где m0 (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального
момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа m0=50 мг.
Период его полураспада T=5 мин.
Через сколько минут масса изотопа будет равна 12,5 мг?
a) 11
b) 15
c) 10
d) 30
e) 21
18. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, имеют длины 3, 4
и 12.
Найдите длину диагонали этого прямоугольного параллелепипеда.
a) 17
b) 15
c) 10
d) 13
e) 12
19. В понедельник акции компании подорожали на некоторое число процентов, а во вторник
подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем
при открытии торгов в понедельник. На сколько процентов подорожали акции компании в
понедельник?
a) 14
b) 32
c) 20
d) 25
e) 35
20. Найдите наибольшее значение функции y=x3+2x2+x+3 на отрезке [−3; −0,5].
a) 5
b) 2
c) 3
d) 9
e) 1
21. Решите уравнение sin2x+2cos2x=1.
a) −arctg1+πn, n∈ℤ
2
𝜋
b) − +πn, n∈ ℤ
4
c) −𝜋 +πn, n∈ ℤ
8
d) −𝜋+𝜋𝑛, n∈ ℤ
8
𝜋
2
e) − +2πn, n∈ ℤ
8
𝜋
22. Найти корни sin2x+2cos2x=1 уравнения на промежутке [ 4 ;
a)
b)
c)
d)
e)
5𝜋
4
]
7𝜋 11𝜋
;
8
4
3𝜋 7𝜋
;
8
8
2𝜋 11𝜋
;
8
4
𝜋 𝜋
;
8 4
2𝜋 11𝜋
8
;
8
23. В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD с диагоналями AC=6 и
BD=12. Высота призмы равна √15. Найдите угол между прямыми AB1 и D1C.
a) 65
b) 57
c) 40
d) 30
e) 60
4𝑥−1.5 + 2𝑥−2 ≤ 1
24. Решите систему неравенств: {
log 2 (𝑥 − 3)2 + log √2(3 − 𝑥) < 12
a) (−∞;1]
b)
c)
d)
e)
(−5;1]
(−5;3)
[1;3)
[1;1]
25. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая
в точке с абсциссой x0.
Найдите значение производной функции f(x)в точке x0.
a) 3
b) 5
c) 4
d) 2
e) 0